1. O documento discute a teoria do funcional da densidade (DFT), introduzindo seus principais conceitos e desenvolvimentos. 2. Os teoremas de Hohenberg-Kohn de 1964 estabeleceram os fundamentos da DFT, mostrando que a energia é uma funcional única da densidade eletrônica. 3. As equações de Kohn-Sham de 1965 fornecem um método prático para aplicar a DFT, aproximando o sistema de elétrons em interação por um sistema fictício de partículas independentes.

1. Prof. Dr. José Walkimar M. Carneiro
Dr. Ednilsom Orestes
19 de Abril de 2013
DISCIPLINA
Teoria do Funcional da Densidade
(DFT)

2. 1. Introdução
• Muitos métodos para resolver 𝐻Ψ = 𝐸Ψ.
• Aproxima-se 𝐻 ou Ψ.
• 𝐻: Se grau de aprox. alto – soluções possíveis baixo poder
predição.
Se grau de aprox. baixo – alto poder de predição e
soluções difíceis.
• Ψ é muito difícil de calcular. Ex.: Nitrogênio.
Ψ 𝑁 = Ψ 𝐫1, … , 𝐫7 ; 𝐫={x,y,z}
10 valores para cada coordenada = 107×3
valores (bytes)
CD (700Mb) = 1,4 × 1012
×(1,2mm altura) ≅ 1.714.285,7 Km
CD (1,2mm altura) ≅ 1.714.285,7 Km
~ 4,45 × (dist. Terra-Lua ≅ 385.000 Km)
É possível ir e voltar 2 vezes!
Só armazenar! Condições de contorno

3. 1. Introdução (cont.)
• Talvez o mais bem sucedido Método de Estrutura Eletrônica.
Versatilidade e eficiência com precisão aceitável
• Não há FCI de 100 átomos!
• Paper HK (1964) > 4000 citações.
• Paper KS (1965) > 9000 citações.
• ½ dos 10 + citados na Química.
• 3 + citados 110 anos família PR.
• Átomos, molécular, clusters,
líquidos, sólidos, supercondutores,
relativísticos, biológicos e mineralógicos.
• Nobel 1998: Walter Kohn e John Pople.
Publicações DFT: ISI Web of Science

4. 2. O que é um funcional?
• Função: regra que associa um nº. com cada valor da variável:
𝑓 𝑥 = 𝑥3, associa x=3 com 27.
• Funcional: regra que associa um nº com cada função:
𝐹 𝑓 𝑥 = 𝑥3 𝑑𝑥
2
0
, associa 𝑓 𝑥 = 𝑥3 com 4.
• Outros exemplos: 𝐸 Ψ = Ψ 𝐻 Ψ e Ψ Ψ são funcionais!
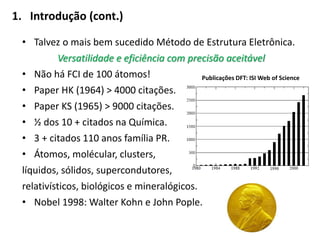
• 𝐹[𝑓](𝑥): Um valor para cada função 𝑓 em cada ponto da
coordenada 𝑥.
• 𝐹[𝑓(𝑥)]: Funcional depende somente da função 𝑓 e não da
sua variável 𝑥.

5. 3. Modelo Thomas-Fermi, 1927
• 1ª idéia usar densidade (antes de HF).
• Base no gás uniforme de elétrons.
𝐸 𝑇𝐹 𝑛 𝐫 = 𝐶 𝐹 (𝑛
5
3(𝐫) − 𝑍) 𝑑𝐫 − 𝑍
𝑛 𝐫
𝑟
𝑑𝐫 +
1
2
𝑛 𝐫1 𝑛(𝐫2)
𝐫1 − 𝐫2
𝑑𝐫1 𝑑𝐫2
• 𝐸0 é resultado de
𝛿𝐸 𝑇𝐹
𝛿𝑛
com restrição de que 𝑛 𝐫 𝑑𝐫 = 𝑁.
• Princípio Variacional para funcionais da densidade: Equação de
Euler-Lagrange.
• Pouca importância cálculos atômicos e moleculares.
• Considerado ancestral da DFT.
+ + + + + + + + + + + + + + +
- - - - - -
- - - - - -
- - - - - -
jellium

6. 4. Teoremas de Hohenberg e Kohn, 1964
• 1º (Parte):
Existe correspondência unívoca (1:1) entre Ψ0 e 𝑛0.
Então, Ψ0 → Ψ0[𝑛0] e portanto todos observáveis também.
Além disso, Ψ0 e 𝑛0 são equivalentes.
Contêm mesma informação! Como é possível?
R. Conhecer 𝑛0 implica conhecer mais que 𝑓(𝐫) arbitrária, mas
sim Ψ0 (resolve a Eq. Schrödinger).
Não há indicação de como determinar 𝑛0 a partir de Ψ0.

7. 4. Teoremas de Hohenberg e Kohn, 1964 (cont.)
• 2ª (Parte):
𝐸 𝑣,0 = 𝐸 𝑣 Ψ0 = Ψ0 𝐻 Ψ0 0
≤ Ψ′
𝐻 Ψ′
= 𝐸 𝑣[Ψ′
].
Usa a 1ª parte: 𝐸 𝑣,0 = 𝐸 𝑣 𝑛0 = Ψ[𝑛0] 𝐻 Ψ[𝑛0] .
Portanto, 𝐸 𝑣 𝑛0 ≤ 𝐸 𝑣 𝑛′
: .
• 3ª (Parte):
𝑇 𝑛 e 𝑈 𝑛 são universais.
• 4ª (Parte):

8. 4. Teoremas de Hohenberg e Kohn, 1964 (cont.)
• Prova 1ª parte via reductio ad absurdum.
• Mecânica Quântica convencional:
𝑣 𝐫
𝐸𝑆
Ψ 𝐫1, … , 𝐫 𝑁
Ψ … Ψ
…
𝑛(𝐫)
…
• Na DFT, temos:
𝑛 𝐫 ⟶ Ψ 𝐫1, … , 𝐫 𝑁 ⟶ 𝑣 𝐫 ⟶
…
…
…
Como otimizar essa quantidade fundamental?

9. 4. Teoremas de Hohenberg e Kohn, 1964 (cont.)
• Prova 1ª parte via reductio ad absurdum.
• Mecânica Quântica convencional:
𝑣 𝐫
𝐸𝑆
Ψ 𝐫1, … , 𝐫 𝑁
Ψ … Ψ
…
𝑛(𝐫)
…
• Na DFT, temos:
𝑛 𝐫 ⟶ Ψ 𝐫1, … , 𝐫 𝑁 ⟶ 𝑣 𝐫 ⟶
…
…
…
Como otimizar essa quantidade fundamental?

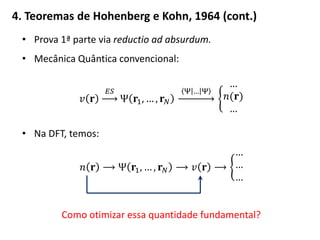
10. 5. Equações de Kohn e Sham, 1965
• 𝐸 totalmente como 𝐸[𝑛]: Modelo Thomas-Fermi.
• Sistema de partículas não-interagentes sob 𝑣 𝑒𝑥𝑡.
• Manter arranjo espacial: 𝒏 𝒓 ≡ 𝒏 𝒔.
𝐸 𝑛 = 𝑇 𝑛 + 𝑈 𝑛 + 𝑉 𝑛 = 𝑇𝑠 𝑛 + 𝑈 𝐻 𝑛 + 𝑣 𝐫 𝑛 𝐫 𝑑𝐫 + 𝐸 𝑥𝑐[𝑛]
onde 𝑇𝑠 𝑛 → 𝑇𝑠 𝜑𝑖 𝑛 = −1
2
𝜑𝑖
∗
𝐫 𝛻2 𝜑𝑖 𝑑𝐫𝑁
𝑖=1
e 𝑈 𝑛 → 𝑈 𝐻 𝑛 = − 𝑞2
2
𝑛 𝐫 𝑛(𝐫′)
𝐫−𝐫′ 𝑑𝐫𝑑𝐫′.
• Portanto:
𝐸 𝑥𝑐 𝑛 = 𝑇 𝑛 − 𝑇𝑠 𝜑𝑖 𝑛 + (𝑈 𝑛 − 𝑈 𝐻[𝑛])

11. 5. Equações de Kohn e Sham, 1965
• Aplicando o Princípio Variacional de HK sobre 𝐸[𝑛]:
ℎ 𝑠
𝐾𝑆 𝜑𝑖 = −
𝛻2
2
+ 𝑣𝑠(𝐫) 𝜑𝑖 = 𝜀𝑖 𝜑𝑖 onde
𝑣𝑠 𝐫 = 𝑣 𝐫 + 𝑣 𝐻(𝐫) + 𝑣 𝑥𝑐 𝐫
com 𝑣 𝐫 = 𝑣 𝐫 𝑛 𝐫 𝑑𝐫 , 𝑣 𝐻 =
𝑛(𝐫)
𝐫 − 𝐫′
𝑑𝐫 , 𝑣 𝑥𝑐 𝐫 =
𝛿𝐸 𝑥𝑐[𝑛]
𝛿𝑛(𝐫)
,
𝑛 𝐫 = 𝜑𝑖 𝐫 2
𝑁
𝑖=1
.
• KS-SCF: aproxima 𝑛 𝐫 e define-se 𝑣𝑠 𝐫 → nova densidade 𝑛′ 𝐫 .
• Muito semelhante ao HF-SCF (troca 𝐅 por 𝐊), exceto por 𝐸 𝑥𝑐.
• 𝜀𝑖 sem significado físico, exceto 𝜀 𝐿𝑈𝑀𝑂 = 𝐸 𝑁−1 − 𝐸 𝑁 (T. Koopmans).
Derivadas parciais
convencionais, 𝜕/𝜕𝑥, são
substituídas por
derivadas funcionais,
𝛿/𝛿𝑥, também parciais.

12. 5. Equações de Kohn e Sham, 1965 (cont.)
• DFT é teoria exata – soluções aproximadas.
• Pode ser “não-empírica” : usando funcionais híbridos.
• HF é teoria aproximada – busca solução exata.
• DFT é variacional até 𝐸 𝑥𝑐 ser aproximada.
• 𝐸 𝐻
𝐵𝑃𝑊91
= −0,5042 𝐻
• Na prática, depende de aproximação para 𝐸 𝑥𝑐.
• 𝐸 𝑥𝑐 carrega todos os efeitos de muitos corpos.
• DFT é consistente com o tamanho.

13. 6. Funcionais de Troca e Correlação
• Definição: 𝐸 𝑥𝑐 𝑛 = 𝑇 − 𝑇𝑠 + (𝑈 − 𝑈 𝐻)
• Na prática: 𝐸 𝑥𝑐 𝑛 = 𝑛 𝐫 𝜀 𝑥𝑐 𝑛 𝐫 𝑑𝐫
soma de contribuições individuais
6.1 Local-Density Approximation
• 𝜀 𝑥𝑐 𝐫 → 𝜀 𝑥𝑐 𝑛 𝐫 onde 𝜀 𝑥 𝑛 𝐫 = −
9𝛼
8
3
𝜋
1
3
𝑛
1
3(𝐫)
• 𝛼 = 2
3 : 𝐸 𝑥𝑐 exata
• 𝛼 = 1 ∶ Slater
• 𝛼 = 3
4 : 𝑋𝛼
• Considerando spin: 𝜀 𝑥 𝑛 𝐫 , 𝜁 → 𝜁 𝐫 = 𝑛 𝛼 𝐫 −𝑛 𝛽 𝐫
𝑛 𝐫
• LDA → LSDA; ℎ𝑖𝜎
𝐾𝑆
onde 𝜎 = ±1; 𝑛 → [𝑛↑, 𝑛↓].
• Correlação: QMC: 𝐸 𝑇
𝑗𝑒𝑙𝑙𝑖𝑢𝑚
para várias densidades.
• VWN (1980): Fitar resultados de 𝐸𝑐. OBS: Vários fits!
• No Gaussian: LDA=Slater+VWN=SVWN (Manual).
• Grid e Performance (gás homogêneo vs. molécula).

14. 6. Funcionais de Troca e Correlação (cont.)
6.2 Gradient-Expansion e Generalized-Gradient Approximation
• 𝜀 𝑥𝑐 𝐫 → 𝜀 𝑥𝑐[𝑛 𝐫 , 𝛻𝑛(𝐫)]
• 𝜀 𝑥/𝑐
𝐺𝐺𝐴
𝑛 𝐫 = 𝜀 𝑥/𝑐
𝐿𝐷𝐴
𝑛 𝐫 +
𝛻𝑛 𝐫
𝑛4/3 𝐫
• Troca: PW; B86; B88, PBE,...
• Correlação: LYP; PW91; P86,...
6.3 Funcionais dos orbitais e não-locais (Meta-GGA)
• Inclui dependência com a densidade de energia cinética, 𝜏.
• 𝜏 𝐫 =
ℏ2
2𝑚
𝛻𝜑𝑖 𝐫 2
𝑖
• Portanto, 𝐸 𝑥𝑐 → 𝐸 𝑥𝑐 𝑛 𝐫 , 𝛻𝑛 𝐫 , 𝜏
• TPSS,...
• Flexibilidade, condições de contorno e SIE.

15. 6.4 Funcionais Híbridos
• Mistura com 𝐸 𝑥
𝐻𝐹
.
𝐸 𝑥𝑐
𝐵3𝑃𝑊91
= 1 − 𝑎 𝐸 𝑥
𝐿𝑆𝐷𝐴
+ 𝑎𝐸 𝑥
𝐻𝐹
+ 𝑏Δ𝐸 𝑥
𝐵
+ 𝐸𝑐
𝐿𝑆𝐷𝐴
+ 𝑐Δ𝐸𝑐
𝑃𝑊91
𝐸 𝑥𝑐
𝐵3𝐿𝑌𝑃
= 1 − 𝑎 𝐸 𝑥
𝐿𝑆𝐷𝐴 + 𝑎𝐸 𝑥
𝐻𝐹 + 𝑏Δ𝐸 𝑥
𝐵 + (1 − 𝑐)𝐸𝑐
𝐿𝑆𝐷𝐴+𝑐Δ𝐸𝑐
𝑃𝑊91
• Parâmetros escolhidos para minimizar o erro médio de
propriedades atômicas e moleculares de conjuntos de sistemas.
• PBEsol, MPWB1K,...
6. Funcionais de Troca e Correlação (cont.)

16. • Determinação propriedades com DFT: Como a propriedade
depende da densidade? Funcional?
• Determinação propriedade com Ψ: Qual o operador mecâno-
quântico correto?
• Todos orbitais KS sujeitos ao mesmo potencial (externo).
• Teorema de Koopmans para o HOMO.
• Orbitais HF sentem potencial diferentes.
• Orbitais virtuais (LUMO) mais fracamente ligados – energia alta e
difusos.
• Estados excitados: combinação linear de determinantes mono,
dupla, tripla,..., enésimo excitados: Φ𝑖
𝑎
, Φ𝑖𝑗
𝑎𝑏
, Φ𝑖𝑗𝑘
𝑎𝑏𝑐
, …
• Teorema HK garante que 𝑛(𝐫) contém todas estas
informações. Mas como extraí-las? TDDFT e etc...
• DFT: 𝑁3 e HF: 𝑁4.
7. Densidade vs. Função de Onda

17. • Limitação: Uso 1 único determinante de Slater. Estrutura de
ressonância.
• Problema: Energia – função da densidade local (estritamente).
• Ruim tratamento forças de London, van der Waals.
• Ruim cálculo de dímeros de Gases Nobres.
8. Limitações e Problemas

18. Energia do estado fundamental do Argônio (Z=18).
9. Performance

19. Momento de dipolo (D).
9. Performance (cont.)
Molécula HF MP2 BLYP B3LYP Exp.
𝑁𝐻3 1,62 1,52 1,48 1,52 1,47
𝐻2 𝑂 1,98 1,85 1,80 1,86 1,85
𝐻𝐹 1,92 1,80 1,75 1,80 1,83
𝑃𝐻3 0,71 0,62 0,59 0,62 0,57
𝐻2 𝑆 1,11 1,03 0,97 1,01 0,97
𝐻𝐶𝑙 1,21 1,14 1,08 1,12 1,11
𝐶𝑂 -0,25 0,31 0,19 0,10 0,11
𝑆𝑂2 1,99 1,54 1,57 1,67 1,63

20. Referências
1. Inhomogeneous Electron Gas, P. Hohenberg and W. Kohn, Phys. Rev. 136, B864
(1964).
2. Self Consistent Equations Including Exchange and Correlation Eects, W. Kohn and
L.J. Sham, Phys. Rev. 140, A1133 (1965).
3. Nobel Lecture: Electronic structure of matter{wave functions and density
functionals, W. Kohn, Rev. Mod. Phys. 71, 1253 (1998).
4. The density functional formalism, its applications and prospects, R.O. Jones and O.
Gunnarsson, Rev. Mod. Phys. 61, 689 (1989).
5. Density-Functional Theory of Atoms and Molecules, R.G Parr and W. Yang, Oxford
University Press, New York (1989).
6. A Bird’s-Eye View of Density-Functional Theory. Klaus Capelle.

21. Exercícios
Energias de atomização são frequentemente difíceis de serem calculadas com precisão,
principalmente com método HF. Calcule a energia de atomização do CO2 usando diferentes
aproximações para o funcional de troca e correlação e função de base 6-31G(d). Otimize a
estrutura e calcule as frequências vibracionais do CO2 para obter a energia de ponto-zero e
então faça um cálculo single-point de energia para o carbono e para o oxigênio
(SCF=Tight). Energia de atomização: 𝐸𝐴0 = 𝐸 𝐶 + 2𝐸 𝑂 − 𝐸 𝐶𝑂2 + 𝑍𝑃𝐸 . Lembre-se que
a multiplicidade do Oxigênio e Carbono atômico é 3. → PORQUE??
http://www.jca.umbc.edu/~george/html/courses/atomic/element_grd_config.shtml
Dióxido de Carbono Carbono Oxigênio EA0 Δ(Exp)
Método R(C-O) E(CO2) ZPE* E E (Kcal/mol)
HF 1,143 -187,63418 0,0127 -37,68086 -74,78393 233,90690 147,99310
SVWN 1,171 -187,61677 0,0115 -37,56616 -74,64334 472,14983 -90,24983
SVWN5 1,172 -187,18193 0,0115 -37,45370 -74,48842 464,28097 -82,38097
BLYP 1,183 -188,56306 0,0111 -37,83202 -75,04696 392,82755 -10,92755
B3LYP 1,169 -188,58094 0,0116 -37,84628 -75,06062 377,64205 4,25795
B3PW91 1,168 -188,50695 0,0117 -37,82569 -75,03133 380,82975 1,07025
MP2 1,180 -188,10775 0,0115 -37,73297 -74,88004 378,50800 3,39200
Exp. 1,162 381,9
* Os valores de Zero-point correction foram encontrados com G09, outras versões podem fornecer números ligeiramente diferentes