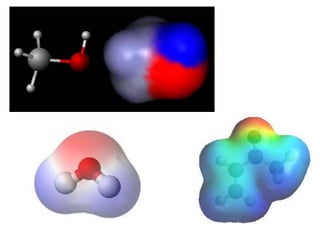
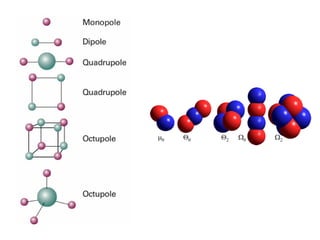
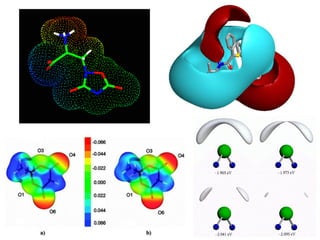
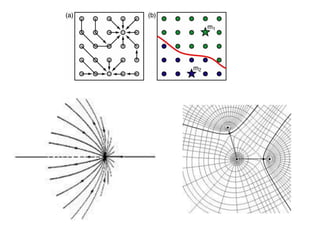
O documento aborda a distribuição de cargas em moléculas e suas propriedades espectroscópicas, discutindo conceitos como momento de multipólo, potencial eletrostático molecular, e cargas atômicas parciais. Inclui metodologias teóricas e experimentais para avaliar polarizabilidade, ionização e espectroscopia molecular. A análise também se estende à comparação de diferentes modelos de cálculo e suas aplicações na química computacional.

1. Prof. Dr. José Walkimar M. Carneiro
Dr. Ednilsom Orestes
02 de Maio de 2013
DISCIPLINA
Distribuição de Cargas e
Propriedades Espectroscópicas

2. 1. Introdução
• Molécula: arranjo espacial de núcleos ligados por elétrons.
• Distribuição carga diz a localização dos elétrons na molécula.
• Difícil de se obter experimentalmente.
• Formalmente responsável por TODAS as propriedades
• Dois tipos de propriedades:
⁻ Medidas diretas de distribuição de carga.
⁻ Medidas extraídas (derivadas) da distribuição de cargas, como
frequências vibracionais e rotacionais.
• Como distribuir os elétrons em torno dos núcleos?
• Não há maneira única.
• Difícil avaliar qualidade dos métodos teóricos → MULTIPÓLOS

4. 2. Momento de Multipólo Elétrico
𝐱 𝑘
𝐲 𝑙
𝐳 𝑚
= 𝑍𝑖 𝑥𝑖
𝑘
𝑦𝑖
𝑙
𝑧𝑖
𝑚
nuc
𝑖
− 𝜓𝑗 𝐫𝑗 𝑥𝑗
𝑘
𝑦𝑗
𝑙
𝑧𝑗
𝑚
𝜓𝑗 𝐫𝑗 𝑑𝐫𝑗
el
𝑗
• Momento de monopólo:
⁻ (𝑘 = 𝑙 = 𝑚 = 0).
⁻ 𝟏 = 𝑍𝑖
át
𝑖 − 𝜓𝑗 𝐫𝑗 𝜓𝑗 𝐫𝑗 𝑑𝐫𝑗
el
𝑗
⁻ (carga molecular) = (soma das cargas nucleares) - (no. de elétrons).
• Momento de dipólo (𝑘, 𝑙 ou 𝑚 = 1):
⁻ Experimentalmente mede-se magnitude total:
𝜇 = 𝜇 𝑥
2 + 𝜇 𝑦
2
+ 𝜇 𝑧
2
⁻ 𝜇 = (distrib. de cargas positivas) – (distrib. de cargas negativas)
⁻ Interação intermolecular a longas distâncias é aproximada por
interações entre multipólos (Expansão de Taylor).

6. 3. Potencial Eletrostático Molecular
𝑉 𝑀𝐸𝑃 𝐫 =
𝑍 𝑘
𝐫 − 𝐫𝑘
−
nuc
𝑘
Ψ 𝐫′
𝟏
𝐫 − 𝐫′
Ψ 𝐫′ 𝑑𝐫′
• Grau de atração ou repulsão de cargas positivas ou negativas.
• Não assume polarização da molécula (resposta à carga).
• Experimentalmente difícil, computacionalmente fácil.
• Informação sobre polaridade local em cada região do espaço.
• Predizer locais de maior reatividade química.

8. 4. Cargas Atômicas Parciais – Análise Populacional
• Errado associar polaridade molecular (onda) com acúmulo ou
deficiência de carga em átomos individuais (partícula).
• Não há forma universal de calcular cargas atômicas parciais.
⁻ Usada de diferentes maneiras em diferentes modelos qualitativos e
quantitativos.
Mulliken (1955)
• Partição Ψ em contrib. atômicas (peso de cada orbital).
𝑁 = 𝜓𝑗 𝐫𝑗 𝜓𝑗 𝐫𝑗 𝑑𝐫𝑗
el
𝑗
= 𝑐𝑗𝑟 𝜑 𝑟 𝐫𝑗 𝑐𝑗𝑠 𝜑𝑠 𝐫𝑗 𝑑𝐫𝑗
𝑟,𝑠
el
𝑗
= 𝑐𝑗𝑟
2
+ 𝑐𝑗𝑟 𝑐𝑗𝑠 𝐒 𝑟𝑠
𝑟≠𝑠𝑟
el
𝑗
• Muito sensível ao tamanho da função de base.

9. 4. Cargas Atômicas Parciais – Análise Populacional (cont.)
Löwdin, 1970
• Análise populacional somente com 𝜑 ortogonais.
• Ortogonalização simétrica, “deforma” todos os orbitais.
Natural Population Analysis (NPA), 1985
• Ortogonalização em vários estágios.
• Converge com aumento do tamanho da função de base.
Generalized Atomic Polar Tensor (GAPT), 1989
• Baseado análise de observáveis físicos calculados com Ψ.
𝑞 𝑘 +
1
3
𝜕𝜇 𝑥
𝜕𝑥 𝑘
+
𝜕𝜇 𝑦
𝜕𝑦 𝑘
+
𝜕𝜇 𝑧
𝜕𝑧 𝑘
• Depende da qualidade com que se calcula 𝜇

10. 4. Cargas Atômicas Parciais – Análise Populacional (cont.)
Generalized Atomic Polar Tensor (GAPT), 1989
• Depende da qualidade com que se calcula 𝜇.
• Computacionalmente, equivalente ao cálculo de frequências.
• Pode usar 𝜌(𝐫) (dados de Raio-X) no lugar de 𝜇.
Atoms-In-Molecules, Bader 1990
• Partição baseada na superfície de fluxo zero para cada núcleo.
𝛻𝜌 ∙ 𝐧 = 0
Charges from Eletrostatical Potencial (CHELPG), 1990
• Partição baseada no potencial eletrostático (MEP).
• Propriedade mais óbvia para cálculo cargas parciais.

12. 5. Polarizabilidade e Hiperpolarizabilidade
• Polizabilidade, 𝛼: Variação do momento do dipólo por unidade
de força do campo elétrico aplicado.
𝛼 =
𝜕𝜇
𝜕𝐄
• Molécula isolada no vácuo → 𝜇0.
• Dipólo induzido = 𝜇0 − 𝜇 𝐄
• Experimentalmente: variação da energia com o campo elétrico
(Efeito Stark).
• Quando 𝐄 é fraco: inclinação da reta → 𝜇0.
• Quando 𝐄 é forte: dependência quadrática, 𝜇 aumenta com 𝛼.
• Quando 𝐄 é ainda mais forte: dependência cúbica → 𝛽

13. 6. Polarizabilidade e Hiperpolarizabilidade
• Medidas espectrais: resultado de mudanças na energia em
resposta a alguma perturbação externa.
𝐸 𝐗 = 𝐸 𝟎 +
𝜕𝐸
𝜕𝐗 𝐗=0
∙ 𝐗 +
1
2!
𝜕2 𝐸
𝜕𝐗2
𝐗=0
∙ 𝐗2 +
1
3!
𝜕3 𝐸
𝜕𝐗3
𝐗=0
∙ 𝐗3 + ⋯
𝜇0 𝛼 𝛽
• Usando 𝐁: Mom. mag. perm., magnetizab. e suscept. magnética.
7. Potenciais de Ionização e Afinidade Eletrônica
• Koopmans: 𝐼𝑃 ⟷ 𝐻𝑂𝑀𝑂 ( e 𝐸𝐴 ⟷ 𝐿𝑈𝑀𝑂)
• Alternativa: calcular 𝐸 𝑇 da espécie antes e depois da ionização.
⁻ Mais rigorosa.
⁻ Ionização vertical: geometria após ionização é idêntica geometria antes.
⁻ Ionização adiabática: geometria após ionização é reotimizada (relaxada).

14. 8. Espectroscopia
• Com PES → Resolver Eq. Schrödinger para movimento dos
núcleos.
−
1
2𝑚𝑖
𝑁
𝑖
𝛻𝑖
2
+ 𝑉 𝐪 Ξ 𝐪 = 𝐸(𝐪)
• Solução fornece dados de espectroscópicos (rot. & vib.).
Rotacional
• Aprox. rotor rígido: geometria constante no equilíbrio.
• 𝑉(𝐪eq) → constante multiplicativa.
• Molécula diatômica heteronuclear
(espectro rotacional é observado quando existe momento de dipólo)
• Linhas espectro depende momento de inércia (geometria
molecular).

15. 8. Espectroscopia (cont.)
Vibracional
• Transições ocorrem na região do infravermelho.
• Altamente localizadas na molécula.
• Espaçamento similar entre níveis.
• Muito usado na determinação estrutural.
• Importante: otimização de geometria e estados excitados.
• Base para maioria das pesquisas em química computacional.
• Molécula diatômica: movimento vibracional é função de 𝑟.
• Não se conhece 𝑉(𝐪).
• Eq. Schrödinger para vários pontos – fitting (polinomial, Morse, etc.)
• Função de 3N variáveis (incluindo transl. e rot.).

16. 8. Espectroscopia (cont.)
Vibracional (cont.)
• Oscilador harmônico.
• Considerando 𝑈 𝑟𝑖𝑗 = 1
2 𝑘𝑖𝑗 𝑟𝑖𝑗 − 𝑟𝑖𝑗,eq
2
−
1
2𝜇
𝜕2
𝜕𝑟2
+
1
2
𝑘 𝑟 − 𝑟eq
2
Ξ 𝒓 = 𝐸 𝑟 Ξ 𝒓
𝐸 = 𝑛 +
1
2
ℎ𝜔 onde 𝜔 =
1
2𝜋
𝑘
𝜇
e Δ𝑛 = ±1, ±2, ±3, …
• Separação entre níveis adjacentes = ℎ𝜔 !!
• Necessário somente:
𝜕2 𝐸
𝜕𝑟eq
2
• Derivada analítica disponível para HF, MP2, DFT, QCISD, CCSD, etc.
• Erro: expansão de Taylor truncada.
• Separação entre níveis diminui com aumento do no. quântico.

21. Exercício. Determine: (a) o valor da carga (Mulliken e CHELPG) dos
átomos de carbono da ligação dupla; (b) o momento de dipolo de cada
uma das moléculas; (c) o modo vibracional associado à ligação dupla C=C
em cada molécula; e (d) a energia dos HOMO e LUMO da seguinte série
de vinís com B3LYP e 6-31+G(d).
C
C
H H
HH
C
C
H H
FH
C
C
H H
OHH
C
C
H H
CH3H
C
C
H H
NH2H
Etileno Fluoroetileno Vinil Álcool Propeno Vinil Amina
Carga C1 Carga C2 Dipolo Freq C=C En. HOMO En. LUMO
Mull CHelpG Mull CHelpG
Etileno
Fluoroetileno
Vinil Álcool
Propeno
Vinil Amina
Utilize: # B3LYP/6-31+G(d) Opt Freq Pop=CHelpG
Salvar a figura dos orbitais (isovalue=0,05) e do espectro de IR.