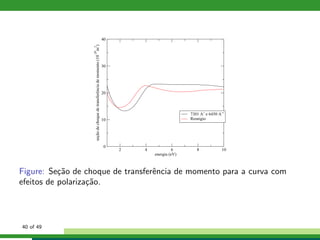
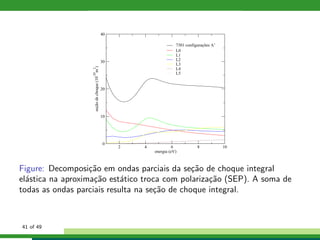
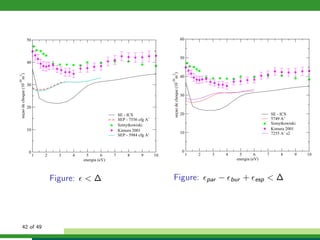
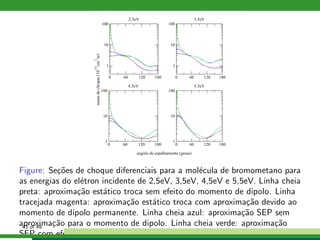
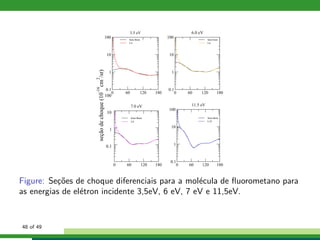
Este documento descreve um estudo sobre colisões de elétrons com moléculas de CH3X, onde X pode ser F, Cl, Br ou I. Apresenta os métodos teóricos utilizados como Hartree-Fock-Roothaan, pseudopotenciais, equação de Lippmann-Schwinger e método multicanal de Schwinger. Também descreve os resultados obtidos para espalhamento elástico e excitação vibracional nestas colisões.

1. Colis˜oes de el´etrons com mol´eculas de CH3X ( X = F, Cl, Br,
I): espalhamento el´astico e excita¸c˜ao vibracional
Luciana Cristine Silva Amorim

2. Conte´udo
• Motiva¸c˜ao
• Descri¸c˜ao te´orica
◦ O M´etodo de Hartree-Fock-Roothaan
◦ Pseudopotenciais
◦ Espalhamento por um potencial
◦ O M´etodo das ondas parciais
◦ Ressonˆancias
◦ Equa¸c˜ao de Lippmann-Schwinger
◦ Princ´ıpio variacional de Schwinger
◦ M´etodo Multicanal de Schwinger (SMC)
◦ Constru¸c˜ao do espa¸co de configura¸c˜oes
◦ Orbitais Virtuais Modificados
• Resultados
• Conclus˜oes e perspectivas futuras
2 of 49

3. O M´etodo de Hartree-Fock-Roothaan
Dentro da aproxima¸c˜ao de Born-Oppenheimer, onde consideramos
que os n´ucleos que comp˜oem o alvo molecular est˜ao fixos podemos
escrever o seguinte Hamiltoniano eletrˆonico
H = −
N
i=1
∇2
i
2
+
N
i=1
M
A=1
ZA
|ri − rA|
+
1
2
N
i=j
1
|ri − rj |
. (1)
Pela teoria de Hartree-Fock, desejamos encontrar um conjunto de
spin-orbitais χa tais que o determinante formado a partir por estes
spins-orbitais seja a melhor aproxima¸c˜ao poss´ıvel para o estado
fundamental de N-el´etrons descrito pelo Hamiltoniano eletrˆonico esta
aproxima¸c˜ao ´e obtida pelo m´etodo variacional
E0 =
Ψ0|ˆHtro|Ψ0
Ψ0|Ψ0
. (2)
3 of 49

4. • Onde |Ψ0 ´e a fun¸c˜ao de onda antissim´etrica descrita em termos
dos spin-orbitais |Ψ0 = |χ1χ2...χaχb....χN . Cada spin-orbital ´e
constitu´ıdo por uma parte espacial de ψ(ri ) e as fun¸c˜oes que
correspondem aos spins de α(ω) para spin-up e β(ω) para
spin-down.
• Para sistemas com camada fechada, podemos utilizar a
aproxima¸c˜ao de que a parte espacial de cada orbital de spin ´e a
mesma para as diferentes fun¸c˜oes por isto, em vez de resolver o
problema de Hartree-Fock devemos resolver o problema de
Hartree-Fock restrito.
• Realizamos isto aplicando pequenas varia¸c˜oes na fun¸c˜ao de onda
do estado fundamental dos N-el´etrons, |Ψ0 → |Ψ0 + δ|Ψ0 , e o
valor para a energia m´ınima ´e obtido fazendo de E0 um funcional
dos orbitais espaciais ψ(ra). (Sylvio Canuto, Attila Szabo) [2, 1]
4 of 49

5. • Para aplicar o m´etodo variacional impomos a condi¸c˜ao de que
δE0[Ψ0] = 0 assim a energia total ser´a estacion´aria em rela¸c˜ao a
qualquer varia¸c˜ao de |Ψ0 em E0[Ψ0] = Ψ0|ˆHtro |Ψ0 .
• Sabendo que o conjunto de orbitais moleculares formam um
conjunto ortonormal ψi |ψj = δij Impomos a condi¸c˜ao de que
δE0[Ψ0] = 0 para que a energia total seja estacion´aria em rela¸c˜ao
a qualquer varia¸c˜ao de |Ψ0 .
• Obtemos um sistema de N equa¸c˜oes integro-diferenciais acopladas
n˜ao lineares com a forma
f (1)ψ(ri ) = εψ(ri ) , (3)
onde f ´e o operador de Fock para camada fechada (S=0, singleto)
e possui a forma
f (1) = h(1) +
N/2
a
(2Ja(1) − Ka(1)) . (4)
5 of 49

6. A solu¸c˜ao do problema de autovalor (3) ´e um conjunto ortonormal de
orbitais espaciais com energia εa e estes orbitais podem estar
ocupados ou vazios.
A energia eletrˆonica do alvo como fun¸c˜ao destes orbitais moleculares
espaciais pode ser descrita como
E0 = 2
a
haa +
a b
2Jab − Kab , (5)
Os ´ındices 1 e 2 e a, b = 1, 2....N/2 representam as coordenadas
espaciais dos el´etrons 1 e 2. Para resolvermos as equa¸c˜oes (3) de
Fock, utilizamos a contribui¸c˜ao de Roothaan introduzindo orbitais
moleculares como uma combina¸c˜ao linear de orbitais atˆomicos
ψi =
k
µ
Cµ i φµ . (6)
Os orbitais atˆomicos φµ s˜ao representados por combina¸c˜oes lineares
de fun¸c˜oes gaussianas cartesianas
6 of 49

7. f (r, r0, l, m, n, α) = Nα(x − x0)l
(y − y0)m
(z − z0)n
e−α(r−r0)2
. (7)
Por´en estas fun¸c˜oes n˜ao s˜ao ortonormais, havendo entre elas um
overlap dado por Sµν = dr1φµ(r1)φν(r1). A expans˜ao dos orbitais
moleculares em orbitais atˆomicos ´e que transforma as equa¸c˜oes de
Hartree-Fock (3) nas equa¸c˜oes de Hartree-Fock-Roothaan
k
ν=1
FµνCνi = εi
k
ν=1
SµνCνi , (8)
onde i = 1, 2, ..., k, Cνi ´e a matriz quadrada dos coeficientes da
expans˜ao. Os elementos de matriz de (8) s˜ao definidos como
Fµν = Hnucl
µν + Gµν Hnucl
µν = Tµν + V nucl
µν , (9)
Gµν =
λσ
Pλσ[(µν|σλ) −
1
2
(µλ|σν)] , (10)
7 of 49

8. onde definimos o operador de densidade como
Pλσ = 2
N/2
i=1
Cλi Cσi . (11)
Tµν = dr1φν(r1)[−
∇2
1
2
φν](r1) , (12)
V nucl
µν = dr1φµ(r1)[
M
A=1
−
ZA
|r1 − rA|
]φν(r1) (13)
e a integral de dois el´etrons
(µν|σλ) = dr1dr2φµ(r1)φν(r1)
1
|r1 − r2|
φλ(r2)φσ(r2) . (14)
8 of 49

9. Como vimos, o operador de Fock depende dos orbitais espaciais ψ′
i s,
logo o operador s´o ´e determinado quando os orbitais espaciais
tamb´em s˜ao. Ent˜ao o processo utilizado para resolver a equa¸c˜ao de
Hartree-Fock-Roothaan ´e o processo interativo chamado de campo
autoconsistente (Self-Consistent-Field - SFC).Como vemos em (9) o
operador de Fock depende dos orbitais a determinar, desta meneira ´e
feita uma escolha inicial para estes orbitais. Feito isto resolvemos (8)
onde s˜ao determinados os autovalores do problema, desta maneira
constru´ımos um novo operador de Fock. Assim sendo, se repete o
processo interativo at´e se obter uma autoconsistˆencia entre o valor de
entrada e o valor de sa´ıda para a matriz de popula¸c˜ao, por exempo,
ou a energia [2].
9 of 49

10. Pseudopotenciais
Para reduzir o n´umero de el´etrons bem como o n´umero de fun¸c˜oes
gaussianas cartesianas utilizamos o pseudopotencial tanto nos c´alculos
de estrutura eletrˆonica quanto nos c´alculos de espalhamento. As
fun¸c˜oes de onda de valˆencia s˜ao iguais as fun¸c˜oes de onda de todos os
el´etrons a partir de um raio de caro¸co rc. [2]. Os pseudopotenciais de
Bachelet, Hamann e Schl¨uter (BHS) s˜ao descritos
ˆVPP = ˆVcaro¸co + ˆVion , (15)
este operador relaciona o potencial de caro¸co com o potencial dos
el´etrons de valˆencia. A introdu¸c˜ao dos pseudopotenciais no m´etodo
multicanal de Schwinger SMC foi realizado por Bettega et. al. [?]
criando assim o m´etodo Multicanal de Schwinger com
Pseudopotenciais (SMCPP) gerando deste modo uma t´ecnica a qual
reduz o custo computacional.
10 of 49

11. Espalhamento por um potencial
A intera¸c˜ao entre um el´etron de baixa energia e uma mol´ecula ´e
considerado um problema composto por N + 1 corpos. Na
colis˜ao entre part´ıculas podem ocorrer varias possibilidades:
A + B → A + B A + B → A′
+ B (16)
A + B → C + D A + B → C1 + ... + CN (17)
A + B −→ C (18)
A cada uma destas possibilidades chamamos de canal.
Pode ocorrer tamb´em a forma¸c˜ao de ressonˆancias pois, durante
uma colis˜ao, ´e poss´ıvel que o el´etron incidente fique aprisionado
tempor´ariamente no alvo molecular formando o metaest´avel.
11 of 49

12. Figure: Descrevemos o Hamiltoniano do problema como H = p2
2m + V (r)
O movimento de uma part´ıcula de massa m que interage com um
potencial V ´e descrito pela equa¸c˜ao de Schr¨odinger independente do
tempo.
− 2∇2
2m
ψk (r) + V (r)ψk (r) = Eψk (r) (19)
12 of 49

13. • Sendo V (r) finito, ent˜ao para r muito grande (20) ir´a se reduzir a
equa¸c˜ao da part´ıcula livre.
• Uma onda esf´erica emergindo do alvo, para r → ∞ ir´a possuir a
forma assint´otica ψs ∼ Af (θ, φ)eikr /r. Portanto a solu¸c˜ao de 20
que obedece a condi¸c˜ao assint´otica de contorno ´e dada por
ψ(r) → Aeiki r
+ f (θ, φ)
eikr
r
(20)
• Um dos argumentos que permite explicar esta rela¸c˜ao est´a em
interpretar o fluxo da onda esf´erica emergente, na regi˜ao
assint´otica, como o fluxo de part´ıculas espalhadas pelo potencial.
Dentro desta aproxima¸c˜ao, a se¸c˜ao de choque deve ser definida
como a corrente da onda espalhada que passa atrav´es do ˆangulo
s´olido dΩ dividida pelo fluxo da onda incidente e isto nos permite
definir a se¸c˜ao de choque como fun¸c˜ao da amplitude de
espalhamento
dσ
dΩ
= |f (θ, φ)|2
. (21)
13 of 49

14. O M´etodo das ondas parciais
Vamos resolver o problema de espalhamento por um potencial central
via equa¸c˜ao de Schr¨odinger independente do tempo por´em agora o
problema ser´a resolvido em coordenadas esf´ericas.
No caso do potencial central os operadores H, L2, Lz comutam entre
s´ı, logo temos que as autofun¸c˜oes s˜ao comuns a todos os trˆes
operadores. O operador L2 ´e uma constante de movimento e possui
autofun¸c˜oes comuns com uma componente de L, Lz
L2
Y m
ℓ (θ, φ) = ℓ(ℓ + 1)Y m
ℓ , Lz Y m
ℓ (θ, φ) = m(θ, φ) . (22)
Podemos expandir a fun¸c˜ao de onda de espalhamento em ondas
parciais ℓ e m
ψk (r) =
∞
ℓ=0
ℓ
m=−ℓ
Cℓm(k)Rℓ(k, r)Y m
ℓ (θ, φ) , (23)
14 of 49

15. Substitu´ındo (24) na equa¸c˜ao de Schr¨odinger encontramos a equa¸c˜ao
radial
d2
dr2
−
ℓ(ℓ + 1)
r2
− 2V (r) + k2
uℓ(k, r) = 0 , (24)
Se aplicarmos condi¸c˜oes de contorno, para que a solu¸c˜ao de (25)
satisfa¸ca `a condi¸c˜ao assint´otica e comparando com (21), obtemos a
equa¸c˜ao para amplitude de espalhamento
f (k, θ) =
1
k
∞
ℓ
(2ℓ + 1)eiδℓ
sin δℓ(k)Pℓ(cos θ) , (25)
Substitu´ındo a amplitude de espalhamento em (22) podemos obter a
seguinte rela¸c˜ao para a se¸c˜ao de choque
σtot(k) =
4π
k2
∞
ℓ
(2ℓ + 1) sin2
δℓ(k) . (26)
15 of 49

16. Existe uma rela¸c˜ao importante entre a se¸c˜ao de choque total (22) e a
amplitude de espalhamento (28) na dire¸c˜ao frontal θ = 0 fazendo
ent˜ao Pℓ = 1 em (28) podemos escrever
f (k, θ = 0) =
1
k
∞
ℓ=0
(2ℓ + 1)(cos δℓ sin δℓ + i sin2
δℓ) , (27)
onde por compara¸c˜ao chegamos ao teorema ´optico
σtot =
4π
k
Im f (θ = 0) . (28)
A interferˆencia destas duas ondas (onda plana e a onda emergente)
em (θ = 0) deve cancelar parte suficiente corrente incidente de modo
a compensar toda a corrente espalhada, medida pela se¸c˜ao de choque
total.
16 of 49

17. Figure: Representa¸c˜ao
Se¸c˜ao de choque de transferˆencia de momento linear
σMT = dΩ(1 − cos θ)|fk(θ)|2
=
4π
k2
∞
ℓ=0
(ℓ + 1) sin2
(δℓ+1 − δℓ) ,(29)
onde o fator (1 − cos θ) garante que as part´ıculas espalhadas na
dire¸c˜ao frontal (θ ∼ 0) sejam ignorados e d´a maior valor as part´ıculas
que transferem mais momento ao alvo, quando (θ ∼ π).
17 of 49

18. Ressonˆancias
Uma ressonˆancia de forma, precisa da combina¸c˜ao do potencial de
intera¸c˜ao entre o alvo e a part´ıcula incidente V (r) e a barreira de
momento angular ℓ(ℓ + 1)/r2, estes formam o potencial efetivo
percebido pela part´ıcula.
Figure: Forma simplificada de representar uma ressonˆancia de forma.18 of 49

19. A importˆancia das ressonˆancias no estudo das colis˜oes entre el´etrons e
mol´eculas est´a centrada no fato de que existem v´arios processos que
possuem como processo intermedi´ario a forma¸c˜ao de um ˆanion
metaest´avel, s˜ao eles a excita¸c˜ao vibracional e dissocia¸c˜ao molecular.
19 of 49

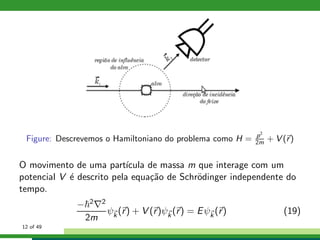
20. Equa¸c˜ao de Lippmann-Schwinger
Para um problema de espalhamento de uma part´ıcula por um
potencial V , a equa¸c˜ao de Schr¨odinger independente do tempo pode
ser escrita como
[∇2
r + k2
]ψ(k, r) = V (r)ψ(k, r) (30)
A solu¸c˜ao desta equa¸c˜ao n˜ao homogˆenea ´e da forma
|ψ
(±)
ki
= |Ski
+ G
(±)
0 V |ψ
(±)
ki
, (31)
a fun¸c˜ao de Green deve satisfazer a equa¸c˜ao de Helmholtz e pode ser
escrito na forma
G
(±)
0 =
1
E − H0 ± iε
. (32)
20 of 49

21. Vamos escrever (32) na representa¸c˜ao de coordenadas e para isto
vamos projet´a-la na base |r e teremos a equa¸c˜ao de
Lippmann-Schwinger na forma integral,
ψ
(±)
ki
(r) = φki
(r) + d3
r′
G
(±)
0 (r, r′
)V (r, r′
)ψ
(±)
ki
(r) . (33)
Podemos introduzir um conjunto completo de ondas planas em (33)
G
(±)
0 = −(2π)−3
lim
ε→0+
eik.(r−r′)
k′2 − k2 ∓ iε
. (34)
levando em conta que ε ´e muito pequeno podemos resolver a integral,
pelo m ’etodo dos res´ıduos [?], chegando assim na fun¸c˜ao de Green
para a part´ıcula livre
G
(±)
0 (r, r′
) = −
1
4π
e(±)ik.|r−r′|
|r − r′|
. (35)
21 of 49

22. Substitu´ındo (36) na equa¸c˜ao integral de Lippmann-Schwinger (34) e,
fazendo r tender a infinito obtemos como limite assint´otico
ψ
(±)
ki
(r) → Ski
−
eikr
4πr
dr e−ik′.r
V (r′
)ψ
(±)
ki
(r′
) . (36)
Comparando (37) com a equa¸c˜ao (21), a qual representa o
comportamento da fun¸c˜ao de onda de espalhamento em sua forma
assint´otica fora da regi˜ao de influˆencia do alvo, ver figura 1, e sendo
f (θ, φ) obtemos uma express˜ao para a amplitude de espalhamento
f = −2π2
Skf
|V |ψ
(+)
ki
= −2π2
ψ
(−)
kf
|V |Ski
, (37)
Como estamos tratando de um problema de colis˜ao el´astica, o m´odulo
do vetor de onda do el´etron incidente ´e igual ao m´odulo do el´etron
espalhado |ki | = |kf | = k, ocorrendo apenas a mudan¸ca de dire¸c˜ao.
22 of 49

23. Princ´ıpio variacional de Schwinger
Para obter a amplitude de espalhamento a partir da equa¸c˜ao de
Lippmann-Schwinger usamos o m´etodo variacional, onde escrevemos
a amplitude de espalhamento na forma de um funcional em termos da
fun¸c˜ao de onda [3].
V |ψ
(±)
ki
= V |Ski
+ VG
(±)
0 U|ψ
(±)
ki
. (38)
Isolamos o termo V |Ski
e substitu´ımos na equa¸c˜ao (38) para a
amplitude de espalhamento, deste modo obtemos
f = −2π2
ψ
(−)
kf
|V − VG
(+)
0 |ψ
(+)
ki
, (39)
onde somando as duas defini¸c˜oes para a amplitude de espalhamento e
subtra´ındo (40) obtemos mais uma express˜ao chamada de forma
bilinear do Princ´ıpio Variacional de Schwinger (PVS)
[f ] = −2π2
Skf
|V |ψ
(+)
ki
+ ψ
(−)
kf
|V |Ski
− ψ
(−)
kf
|V − VG
(+)
0 |ψ
(+)
ki
.(40)23 of 49

24. podemos nos deter em descrever a fun¸c˜ao de onda na regi˜ao de
alcance do potencial. Para isto vamos expandir a fun¸c˜ao de onda em
um conjunto de fun¸c˜oes de base conhecida {χm}
|ψ
(+)
ki
=
m
a
(+)
m (ki )|χm , ψ
(−)
ki
| =
n
a
(−)∗
n (kf ) χn| , (41)
Determinando os coeficiˆentes da expans˜ao determinaremos os
elementos de matriz os quais ser˜ao utilizados posteriormente, para
isto devemos impor que o funcional da amplitude de espalhamento
seja estacion´aria
∂[f ]
∂a
(+)
m (ki )
=
∂[f ]
a
(−)∗
n (kf )
. (42)
Derivando o funcional da amplitude de espalhamento obtemos os
coeficientes am e an.
a
(+)
m (ki ) =
n
(d−1
)mnbn(ki ) , a
(−)∗
m (kf ) =
m
(d−1
)mnb†
m(kf ) , (43)
24 of 49

25. Substitu´ındo os coeficientes determinados em (41) chegamos na
amplitude de espalhamento obtida pelo m´etodo variacional que
corresponde ao princ´ıpio variacional de Schwinger
f = −2π2
m,n
Skf
|V |χn (d−1
)mn χn|V |Ski
, (44)
onde o elemento de matriz dmn ´e definido por
dmn = χm|A(+)
|χn , (45)
onde A(+) = V − VG
(+)
0 V .
Em (57) vemos que a base {χm} esta multiplicada pelo potencial de
intera¸c˜ao temos por consequˆencia que a base precisa ser bem descrita
na regi˜ao do potencial de intera¸c˜ao. Fora desta regi˜ao n˜ao h´a esta
necessidade, como j´a foi mencionado no texto.
25 of 49

26. M´etodo Multicanal de Schwinger (SMC)
• O m´etodo mullticanal de Schwinger foi desenvolvido para o estudo
do espalhamento de el´etrons de baixas energias por mol´eculas de
geometria arbitr´aria. Este m´etodo ´e uma extens˜ao do princ´ıpio
variacional de Schwinger [4, 3].
• O m´etodo ´e ab initio e permite c´alculos de espalhamento el´astico,
a inclus˜ao de efeitos de troca devido a indistinguibilidade dos
el´etrons e a polariza¸c˜ao do alvo devido a presen¸ca do el´etron
incidente.
• Entendemos por polariza¸c˜ao a distor¸c˜ao da nuvem eletrˆonica
causada devido a presen¸ca do el´etron incidente.
• Como estamos considerando a aproxima¸c˜ao de n´ucleos fixos temos
o Hamiltoniano HN+1 descrito como
HN+1 = (HN + TN+1) + V = H0 + V , (46)
26 of 49

27. Utilizamos a equa¸c˜ao de Lippmann-Schwinger para um determinado
canal
ψ
(±)
ki
= Ski
+ G
(±)
0 V ψ
(±)
ki
, (47)
Analizando a equa¸c˜ao (48) temos que o lado esquerdo da equa¸c˜ao ´e
antissim´etrico perante `a troca de el´etrons enquanto que o lado direito
n˜ao. Para resolvermos o problema e garantir a antissimetria da fun¸c˜ao
de onda de espalhamento precisamos incluir os autoestados do
cont´ınuo do alvo molecular na fun¸c˜ao de Green.
P =
N0
ℓ=1
|Φℓ(1, 2, ..., N) Φℓ(1, 2, ..., N)| , (48)
temos ent˜ao a fun¸c˜ao de Green projetada e que inclui os canais
abertos escrita na forma
G
(±)
P =
ℓ
|Φℓ Φℓ|
k2
ℓ
2 − k2
2 ± iε
, (49)
27 of 49

28. Contudo, quando projetamos a equa¸c˜ao de Lippmann-Schwinger no
espa¸co dos canais abertos estamos perdendo a indistinguibilidade
entre o el´etron incidente e os el´etrons do alvo molecular, estamos
perdendo informa¸c˜oes f´ısicas sobre os canais fechados tais como as
excita¸c˜oes virtuais do alvo molecular. Para recuperarmos esta
informa¸c˜ao vamos utilizar o projetor sobre os canais fechados, e assim
teremos uma equa¸c˜ao multicanal.
(1 − aP) , (50)
Podemos realizar uma decomposi¸c˜ao na fun¸c˜ao de onda entre uma
parte que diz respeito a fun¸c˜ao de onda projetada sobre os canais
abertos e, outra parte, sobre os canais fechados do modo
ψ
(+)
ki
= aPψ
(+)
ki
+ (1 − aP)ψ
(+)
ki
(51)
conhecendo a rela¸c˜ao de comuta¸c˜ao [H0, P] = 0 podemos substituir e
manipular (??) de modo a obter a express˜ao multicanal
A(+)
ψ
(+)
ki
= VSki
, (52)
28 of 49

29. onde
A(±)
=
1
2
(PV + VP) − VG
(±)
P V +
1
a
[ˆH −
a
2
(ˆHP + P ˆH)] (53)
Precisamos portanto determinar o parˆametro a para o problema de
espalhamento de el´etrons por um alvo molecular de modo a satisfazer
a condi¸c˜ao A(+)† = A(−). Esta condi¸c˜ao ´e satisfeita contanto que
sejam utilizadas fun¸c˜oes de quadrado integr´avel L2. Isto ocorre
porque o operador Hamiltoniano ˆH n˜ao ´e hermiteano em integrais
que envolvem dois orbitais de espalhamento devido ao operador de
energia cin´etica . Para eliminarmos este problema precisamos impor
que os elementos de matriz abaixo entre fun¸c˜oes de quadrado n˜ao
integr´avel seja nula
χkm
|
1
a
ˆH −
a
2
(ˆHP + P ˆH) |χkm
= 0 , (54)
esta condi¸c˜ao determina que a = N + 1.
Assim sendo temos a vers˜ao final para o operador A(±)
A(±)
=
1
2
(PV + VP) − VG
(±)
P V +
1
N + 1
[ˆH −
N + 1
2
(ˆHP + P ˆH)] (55)29 of 49

30. Determinar um novo A(±) e modifica o elemento de matriz (46).
Logo temos para amplitude de espalhamento
f = −2π2
m,n
Skf
|V |χn (d−1
)mn χn|V |Ski
, dmn = χm|A(±)
|χn .(56)
Podemos determinar todos os elementos de matriz para a amplitude
de espalhamento de modo anal´ıtico, exceto para os termos em que
aparece a fun¸c˜ao de Green na forma [?]
χm|VG
(±)
P |χn . (57)
podemos separar a fun¸c˜ao de Green em uma parte real e outra
imagin´aria
GP
P =
abertos
l
P
∞
0
dk
k2
k2
ℓ
2 − k2
2
dΩk|Φℓ(k) Φℓ(k)| , (58)
GR
P = iπ
abertos
l
dΩk|Φℓ(k) Φℓ(k)| . (59)
30 of 49

31. onde o termo referente ao res´ıduo, chamado de on-shell
χm|VGR
P V |χn = iπ
abertos
l
kℓgℓ
mn(kℓ) , (60)
e o termo referente a principal ou off-shell
χm|VGP
P V |χn =
abertos
l
P
∞
0
dk
k2
k2
ℓ
2 − k2
2
gℓ
mn(k) , (61)
onde
gℓ
mn(k) = dΩk χm|V |Φℓ(k) Φℓ(k)|V |χn . (62)
Na equa¸c˜ao (63) aparecem integrais de dois el´etrons com ondas
planas e fun¸c˜oes gaussianas-cartesianas. Estas integrais representam
um grande esfor¸co computacional, por isto a inclus˜ao dos
pseudopotenciais tem um grande valor para os problemas de
espalhamento de el´etrons por alvos moleculares pois, utilizando
apenas os el´etrons de valˆencia o n´umero de integrais diminui e
podemos trabalhar com mol´eculas que possuem ´atomos mais pesados.31 of 49

32. Constru¸c˜ao do espa¸co de configura¸c˜oes
Num primeiro tipo de aproxima¸c˜ao o espa¸co das configura¸c˜oes ´e
constu´ıdo considerado o efeito de troca entre os el´etrons e o efeito de
intera¸c˜ao coulombiana. Este tipo de aproxima¸c˜ao ´e chamado de
Est´atico-Troca (Static-Exchange-SE), mantemos a nuvem eletrˆonica
do alvo molecular congelada durante o processo de colis˜ao e as
fun¸c˜oes de base para a expans˜ao da fun¸c˜ao de onda de (N+1)
el´etrons possui a forma
|χm = A(N+1)|Φ0 ⊗ |ϕm , (63)
O conjunto formado por v´arios {|χm } ir´a gerar o espa¸co de
configura¸c˜oes e, quanto maior for o espa¸co de configura¸c˜oes melhor
ser´a a descri¸c˜ao da fun¸c˜ao de onda de espalhamento.
32 of 49

33. No outro tipo de aproxima¸c˜ao a constru¸c˜ao de espa¸co de
configura¸c˜oes, al´em das contribui¸c˜oes existentes no caso
est´atico-troca possui tamb´em o efeito da distor¸c˜ao da nuvem
eletrˆonica da mol´ecula causada pela presen¸ca do el´etron do cont´ınuo.
Para este tipo de aproxima¸c˜ao inclu´ımos excita¸c˜oes virtuais simples do
alvo, deste modo o el´etron ´e promovido de um orbital ocupado para
um orbital vazio. O Espa¸co de configura¸c˜oes para c´alculo de
espalhamento el´astico inclu´ındo efeitos de polariza¸c˜ao ´e maior do que
o caso est´atico troca e ´e definido por
|χi = A|Φj ⊗ |ϕµ . (64)
Uma excita¸c˜ao virtual simples significa fazer buracos no alvo,
aniquilando el´etrons de orbitais ocupados (orbitais de buraco) e criar
em orbitais vazios (orbitais de part´ıcula), para cada excita¸c˜ao o
estado de spin pode ser singleto ou tripleto. Este tipo de tratamento
para as excita¸c˜oes simples ´e que nos permite descrever o efeito da
distor¸c˜ao da nuvem eletrˆonica do alvo molecular devido a presen¸ca do
el´etron do cont´ınuo.33 of 49

34. Para o c´alculo da se¸c˜ao de choque de espalhamento com efeitos de
polariza¸c˜ao costuma-se descrever orbitais de part´ıcula e de
espalhamento atrav´es dos orbitais virtuais melhorados (”Improved
Virtual Orbital - IVO’s) ou os orbitais virtuais modificados (”Modified
Virtual Orbitals” - MVO’s). Portanto, cada configura¸c˜ao para o caso
(SEP) est´a representada por um conjunto de orbital de buraco +
orbital de part´ıcula + excita¸c˜ao singleto ou tripleto + orbital de
espalhamento. A partir disto foram adotados dois distintos crit´erios
para gerar o espa¸co das configura¸c˜oes para o c´alculo com polariza¸c˜ao.
• Crit´erio tradicional: a energia ´e escolhida de modo a ser inferior a
energia do orbital de espalhamento e de part´ıcula ǫpar < ∆ e
ǫesp < ∆, onde ǫ ´e a energia do orbital molecular e ∆ ´e a energia
de corte .
• Crit´erio das diferen¸cas: foi adotado um crit´erio de corte de energia
que atua diretamente sobre o n´umero de configura¸c˜oes, s˜ao
consideradas configura¸c˜oes que satisfa¸cam a rela¸c˜ao
ǫpar − ǫbur + ǫesp < ∆, sendo ǫ a energia do orbital molecular
(part´ıcula, buraco ou espalhamento) e ∆ o valor da energia de34 of 49

35. Orbitais Virtuais Modificados
Estes orbitais s˜ao constru´ıdos retirando um orbital duplamente
ocupado da mol´ecula onde o crit´erio para a retirada deste orbital ´e a
sua energia. ´E exclu´ıdo o orbital duplamente ocupado de maior
energia. Quando h´a degenerecˆencia de grau n s˜ao exclu´ıdos n orbitais
duplamente ocupados resultando em uma carga de +2n, preservando
deste modo a simetria da mol´ecula.
´E feita en˜ao a diagonaliza¸c˜ao do operador de Fock (3) para o c´ation
+2n a fim de determinar os orbitais, como estes orbitais s˜ao gerados
para o campo de um c´ation muito positivos eles s˜ao mais compactos
na regi˜ao da mol´ecula, fornecendo uma boa descri¸c˜ao dos efeitos
ressonantes.
35 of 49

36. Born closure
A amplitude de espalhamento dentro da primeira aproxima¸c˜ao de
Born ´e descrita
fki ,kf
= f FBA
(ki , kf ) +
lsmc
l=0
l
m=−l
[f SMCPP
lm (ki , kf ) − f FBA
lm (ki , kf )]Ylm(kf ) ,(65)
onde
f FBA
(ki , kf ) = 2i
D.(ki − kf )
|ki − kf |2
. (66)
´e a express˜ao para a amplitude de espalhamento do potencial do
momento de dipolo dentro da primeira aproxima¸c˜ao de Born (FBA).
As amplitudes de espalhamento (66) e (67) s˜ao expandidas em
harmˆonicos esf´ericos, definindo os coeficientes de expans˜ao. Com a
expans˜ao teremos ondas parciais e um fato a considerar, haver´a uma
onda parcial ℓsmc a partir da qual haver´a contribui¸c˜ao para o dipolo
na se¸c˜ao de choque.
36 of 49

37. 1 2 3 4 5 6 7 8 9 10
10
15
20
25
30
35
seçãodechoque(10
-20
m
2
)
A’ SE
SEP -614 tradicional
SEP - 2029 - tradicional
SEP - 7577 tradicional
CH3Cl A’ Singletos e Tripletos
1 2 3 4 5 6 7 8 9 10
Electron energy (ev)
10
12
14
16
18
20
22
24
seçãodechoque(10
-20
m
2
)
A’ SE
SEP 314 tradicional
SEP - 1100 tradicional
SEP - 3929 tradicional
SEP - 5121
SEP - 7301 tradicional
CH3Cl A’ Singletos
Figure: Diferentes configura¸c˜oes singletos e tripletos e somente singletos
para o CH3Cl, utilizando a polariza¸c˜ao ǫ < ∆.
37 of 49

38. 0 1 2 3 4 5 6 7 8 9 10
Electron energy (eV)
0
10
20
30
40
50
60
Crosssection(10
-20
m
2
)
ICS - SE
7301 A’ e 6450 A’’
5161 A’ 4565 A’’
Szmytkowski
Kimura
Jonnes
Figure: Se¸c˜ao de choque
integral el´astica.
1 2 3 4 5 6
energia (eV)
0
10
20
30
40
seçãodechoque(10
-20
m
2
)
7300 A’ e 6439 A’’ diferenças de energia
7301 A’ e 6450 A’’ε<∆
Figure: Os dois crit´erios de
corte de energia.
38 of 49

39. 0 60 120 180
0.1
1
10
100
1eV
0 60 120 180
0.1
1
10
100
3.2eV
0 60 120 180
0.1
1
10
100
5eV
0 60 120 180
0.1
1
10
100
5.5eV
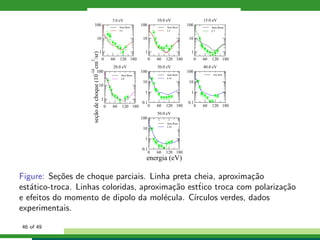
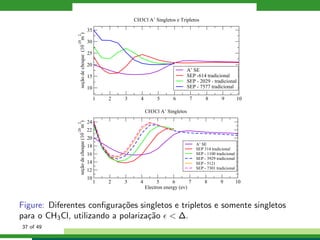
Figure: Se¸c˜oes de choque diferenciais para a mol´ecula de CH3Cl para as
enegias do el´etron incidente 1eV, 3,2eV, 5eV e 5,5eV. Linha cheia em preto:
aproxima¸c˜ao SEP sem incluir efeitos do momento de dipolo. Linhas
coloridas: aproxima¸c˜ao SEP com efeitos de momento de dipolo com cada
lsmc indicado do texto acima. C´ırculos azuis: Dados experimentais [?].
Estrelas rosa: Dados calculados [?]
39 of 49

40. 2 4 6 8 10
energia (eV)
0
10
20
30
40
seçãodechoquedetransferênciademomento(10
-20
m
2
)
7301 A’ e 6450 A’’
Resnigio
Figure: Se¸c˜ao de choque de transferˆencia de momento para a curva com
efeitos de polariza¸c˜ao.
40 of 49

41. 2 4 6 8 10
energia (eV)
0
10
20
30
40
seçãodechoque(10
-20
m
2
)
7301 configurações A’
L0
L1
L2
L3
L4
L5
Figure: Decomposi¸c˜ao em ondas parciais da se¸c˜ao de choque integral
el´astica na aproxima¸c˜ao est´atico troca com polariza¸c˜ao (SEP). A soma de
todas as ondas parciais resulta na se¸c˜ao de choque integral.
41 of 49

42. 1 2 3 4 5 6 7 8 9 10
energia (eV)
0
10
20
30
40
50
seçaodechoque(10
-20
m
2
)
SE - ICS
SEP - 7556 cfg A’
Szmytkowiski
Kimura 2001
SEP - 5984 cfg A’
Figure: ǫ < ∆
1 2 3 4 5 6 7 8 9 10
energia (eV)
0
10
20
30
40
50
60
seçaodechoque(10
-20
m
2
)
SE - ICS
5749 A’
Szmytkowiski
Kimura 2001
7255 A’ s2
Figure: ǫpar − ǫbur + ǫesp < ∆
42 of 49

43. 0 60 120 180
1
10
100
seçaodechoque(10
-16
cm
2
/sr)
2.5eV
0 60 120 180
1
10
100
3.5eV
0 60 120 180
angulo de espalhamento (graus)
1
10
100
4.5eV
0 60 120 180
1
10
100
5.5eV
Figure: Se¸c˜oes de choque diferenciais para a mol´ecula de bromometano para
as energias do el´etron incidente de 2,5eV, 3,5eV, 4,5eV e 5,5eV. Linha cheia
preta: aproxima¸c˜ao est´atico troca sem efeito do momento de dipolo. Linha
tracejada magenta: aproxima¸c˜ao est´atico troca com aproxima¸c˜ao devido ao
momento de dipolo permanente. Linha cheia azul: aproxima¸c˜ao SEP sem
aproxima¸c˜ao para o momento de dipolo. Linha cheia verde: aproxima¸c˜ao
SEP com efeito devido ao momento de dipolo.
43 of 49

44. 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
energia (eV)
0
10
20
30
40
seçãodechoque(10
-20
m
2
)
7556 configurações A’
L0
L1
L2
L3
L4
Figure: Decomposi¸c˜ao em ondas parciais da se¸c˜ao de choque integral
el´astica na aproxima¸c˜ao est´atico troca com polariza¸c˜ao (SEP). Temos maior
contribui¸c˜ao de l = 1.
44 of 49

45. 1 2 3 4 5 6
20
30
40
50
60
70
1 2 3 4 5 6 7 8 9 10
energia
0
10
20
30
40
50
60
70
80
seçaodechoque(10
-20
m
2
)
3797 A’ e 3213 A’’
6626 A’ e 5844 A’’
ICS - SE
Jonnes
Kimura
Szmytkowski
Figure: Se¸c˜ao de choque integral el´astica nas aproxima¸c˜oes est´atico troca
(SE), linha verde, e est´atico troca com polariza¸c˜ao (SEP), linha vermelha e
preta. C´ırculos marrons representam a se¸c˜ao de choque total (TCS) medida
por Szmytkowski, magenta por Kimura e azul por Jonnes
45 of 49

46. 0 60 120 180
1
10
100 Sem Born
L5
5.0 eV
0 60 120 180
1
10
100 Sem Born
L5
10.0 eV
0 60 120 180
1
10
100
seçãodechoque(10
-16
cm
2
/sr)
Sem Born
L8
20.0 eV
0 60 120 180
0.1
1
10
100
Sem Born
L10
30.0 eV
0 60 120 180
1
10
100
Sem Born
L7
15.0 eV
0 60 120 180
energia (eV)
0.1
1
10
100
Sem Born
L10
50.0 eV
0 60 120 180
0.1
1
10
100
Sem Born
40.0 eV
Figure: Se¸c˜oes de choque parciais. Linha preta cheia, aproxima¸c˜ao
est´atico-troca. Linhas coloridas, aproxima¸c˜ao est´tico troca com polariza¸c˜ao
e efeitos do momento de dipolo da mol´ecula. C´ırculos verdes, dados
experimentais.
46 of 49

47. 1 2 3 4 5 6 7 8 9 10 11 12
energia (eV)
0
10
20
30
40
seçãodechoque(10
-20
m
2
)
SEP
SE
experimental
Figure: Se¸c˜ao de choque integral el´astica nas aproxima¸c˜oes est´atico troca
(SE), linha vermelha, e est´atico troca com polariza¸c˜ao (SEP) cuja a escolha
dos orbitais foi feita pelo crit´erio ǫ < ∆, linha azul. C´ırculos verdes
representam a se¸c˜ao de choque total (TCS) medida por Szmytkowski.
47 of 49

48. 0 60 120 180
0.1
1
10
100 Sem Born
L4
3.5 eV
0 60 120 180
0.1
1
10
100 Sem born
L6
6.0 eV
0 60 120 180
0.1
1
10
100
seçãodechoque(10
-16
cm
2
/sr)
Sem Born
L6
7.0 eV
0 60 120 180
0.1
1
10
100
Sem Born
L10
11.5 eV
Figure: Se¸c˜oes de choque diferenciais para a mol´ecula de fluorometano para
as energias de el´etron incidente 3,5eV, 6 eV, 7 eV e 11,5eV.
48 of 49

49. Algumas referˆencias
Attila Szabo e Neil S. Odtlund, Quantum Chemistry, Dover
Publications, Inc. (1996)
Jos´e David M. Vianna, Adalberto Fazzio, Sylvio Canuto.Teoria
Quˆantica de Mol´eculas e S´olidos, Editora Livraria da F´ısica,SP
2004.
M´arcio T. do N. Varella. O M´etodo Multicanal de Schwinger
Aplicado ao Espalhamento de El´etrons I: Aspectos Formais.
Revista Physicae 1 , 45 ,2000.
S. d’A. Sanchez. Tese de Doutorado: O Aprimoramento do
M´etodo Multicanal de Schwinger para o Espalhamento de
P´ositrons por ´Atomos/Mol´eculas, 2008.
49 of 49