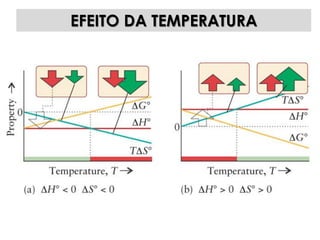
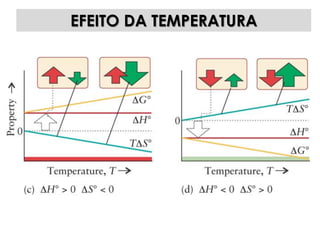
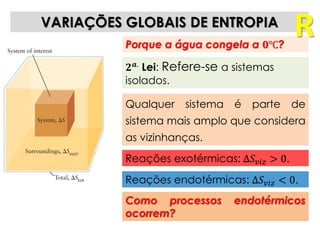
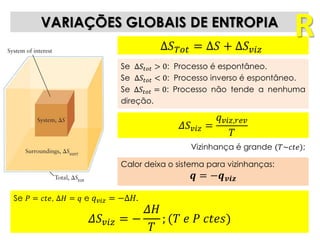
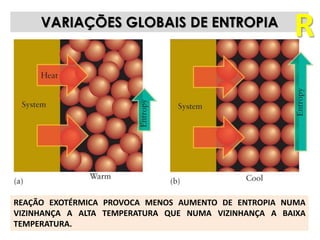
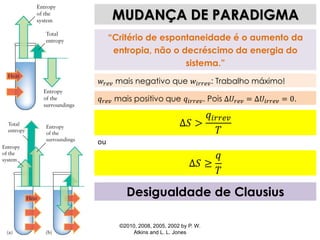
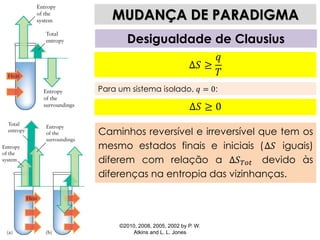
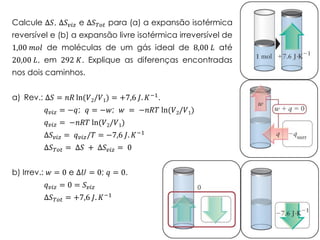
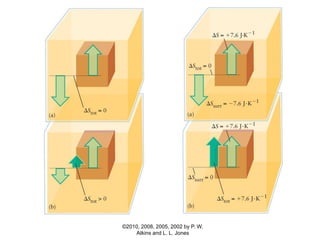
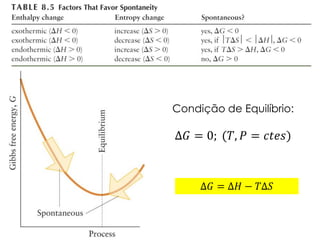
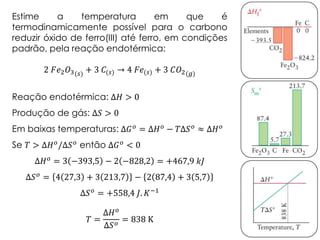
1) O documento discute os conceitos de variação de entropia, variação de entropia da vizinhança e variação de entropia total para determinar a espontaneidade de processos termodinâmicos. 2) É explicado que processos endotérmicos podem ocorrer se a variação de entropia total for positiva, levando em conta a entropia cedida à vizinhança. 3) São apresentados exemplos numéricos de cálculo de variações de entropia para diferentes processos físicos e químicos

1. QUÍMICA GERAL
Escola de Engenharia Industrial Metalúrgica
Universidade Federal Fluminense
Volta Redonda - RJ
Prof. Dr. Ednilsom Orestes
25/04/2016 – 06/08/2016 AULA 16

2. VARIAÇÕES GLOBAIS DE ENTROPIA
Porque a água congela a 𝟎℃?
𝟐 𝒂. Lei: Refere-se a sistemas
isolados.
Qualquer sistema é parte de
sistema mais amplo que considera
as vizinhanças.
Reações exotérmicas: Δ𝑆 𝑣𝑖𝑧 > 0.
Reações endotérmicas: Δ𝑆 𝑣𝑖𝑧 < 0.
Como processos endotérmicos
ocorrem?
R

3. 𝛥𝑆 𝑣𝑖𝑧 =
𝑞 𝑣𝑖𝑧,𝑟𝑒𝑣
𝑇
Se 𝑃 = 𝑐𝑡𝑒, Δ𝐻 = 𝑞 e 𝑞 𝑣𝑖𝑧 = −Δ𝐻.
𝛥𝑆 𝑣𝑖𝑧 = −
𝛥𝐻
𝑇
; (𝑇 𝑒 𝑃 𝑐𝑡𝑒𝑠)
VARIAÇÕES GLOBAIS DE ENTROPIA
Δ𝑆 𝑇𝑜𝑡 = Δ𝑆 + Δ𝑆 𝑣𝑖𝑧
Se Δ𝑆𝑡𝑜𝑡 > 0: Processo é espontâneo.
Se Δ𝑆𝑡𝑜𝑡 < 0: Processo inverso é espontâneo.
Se Δ𝑆𝑡𝑜𝑡 = 0: Processo não tende a nenhuma
direção.
Vizinhança é grande (𝑇~𝑐𝑡𝑒);
Calor deixa o sistema para vizinhanças:
𝒒 = −𝒒 𝒗𝒊𝒛
R

4. VARIAÇÕES GLOBAIS DE ENTROPIA
REAÇÃO EXOTÉRMICA PROVOCA MENOS AUMENTO DE ENTROPIA NUMA
VIZINHANÇA A ALTA TEMPERATURA QUE NUMA VIZINHANÇA A BAIXA
TEMPERATURA.
R

5. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones
Calcule a variação de entropia da
vizinhança quando a água congela em
− 10℃ . Use Δ𝐻𝑓𝑢𝑠 𝐻2 𝑂 = 6,0 𝑘𝐽. 𝑚𝑜𝑙−1 em
− 10℃.
Δ𝐻 𝑐𝑜𝑛𝑔 = − Δ𝐻 𝑓𝑢𝑠
Δ𝑆 𝑉𝐼𝑍 = − Δ𝐻/𝑇 = +23 𝐽 · 𝐾
− 1 · 𝑚𝑜𝑙
− 1
Calcule a variação de entropia da
vizinhança quando 1,00 mol de H2O(l)
vaporiza em 90oC e 1 bar. Considere a
entalpia de vaporização da água como
40,7 kJ·mol-1.
[Resposta: -112 J·K-1]
Calcule a variação de entropia da
vizinhança quando 2,00 mols de NH3(g) se
formam a partir dos elementos em 298 K
R

6. Verifique se a combustão do magnésio é
espontânea, em 25oC, em condições padrão,
sabendo que:
2 𝑀𝑔(𝑠) + 𝑂2(𝑔) ⟶ 2𝑀𝑔𝑂(𝑠)
Δ𝑆 𝑜 = −217 J ∙ K−1
Δ𝐻 𝑜 = −1202 kJ
Δ𝑆 𝑣𝑖𝑧
𝑜
= −
Δ𝐻 𝑜
𝑇
= +4,03 × 103
J ∙ K−1
Δ𝑆𝑡𝑜𝑡
𝑜
= +3,81 × 103
J ∙ K−1
R

7. Será que a formação do fluoreto de hidrogênio a partir de
seus elementos na forma mais estável é espontânea, em 25℃
? Considere a reação 𝐻2(𝑔) + 𝐹2(𝑔) → 2𝐻𝐹(𝑔) Δ𝐻 𝑜 = −542,2 𝑘𝐽 e
Δ𝑆 𝑜
= +14,1 𝐽. 𝐾−1
.
[Resposta: Δ𝑆 𝑣𝑖𝑧 = +1819 𝐽. 𝐾−1 ; portanto, Δ𝑆 𝑇𝑜𝑡 = 1833 𝐽. 𝐾−1 ;
espontânea.
Será que a formação do benzeno a partir de seus elementos
na forma mais estável é espontânea, em 25℃ ? Considere a
reação 6𝐶(𝑔𝑟) + 3𝐻2(𝑔) → 𝐶6 𝐻6(𝑙) , Δ𝐻 𝑜
= +49,0 𝑘𝐽 e Δ𝑆 𝑜
=
− 253,18 𝐽. 𝐾−1.
R

8. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones
Desigualdade de Clausius
MUDANÇA DE PARADIGMA
“Critério de espontaneidade é o aumento da
entropia, não o decréscimo da energia do
sistema.”
𝑤𝑟𝑒𝑣 mais negativo que 𝑤𝑖𝑟𝑟𝑒𝑣: Trabalho máximo!
𝑞 𝑟𝑒𝑣 mais positivo que 𝑞𝑖𝑟𝑟𝑒𝑣. Pois Δ𝑈𝑟𝑒𝑣 = Δ𝑈𝑖𝑟𝑟𝑒𝑣 = 0.
Δ𝑆 >
𝑞𝑖𝑟𝑟𝑒𝑣
𝑇
ou
Δ𝑆 ≥
𝑞
𝑇

9. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones
Caminhos reversível e irreversível que tem os
mesmo estados finais e iniciais (Δ𝑆 iguais)
diferem com relação a Δ𝑆 𝑇𝑜𝑡 devido às
diferenças na entropia das vizinhanças.
MUDANÇA DE PARADIGMA
Desigualdade de Clausius
Δ𝑆 ≥
𝑞
𝑇
Para um sistema isolado, 𝑞 = 0:
Δ𝑆 ≥ 0

10. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones

11. Calcule Δ𝑆, Δ𝑆 𝑣𝑖𝑧 e Δ𝑆 𝑇𝑜𝑡 para (a) a expansão isotérmica
reversível e (b) a expansão livre isotérmica irreversível de
1,00 𝑚𝑜𝑙 de moléculas de um gás ideal de 8,00 𝐿 até
20,00 𝐿, em 292 𝐾. Explique as diferenças encontradas
nos dois caminhos.
a) Rev.: Δ𝑆 = 𝑛𝑅 ln(𝑉2/𝑉1) = +7,6 𝐽. 𝐾−1.
𝑞 𝑣𝑖𝑧 = −𝑞; 𝑞 = −𝑤; 𝑤 = −𝑛𝑅𝑇 ln(𝑉2/𝑉1)
𝑞 𝑣𝑖𝑧 = −𝑛𝑅𝑇 ln(𝑉2/𝑉1)
Δ𝑆 𝑣𝑖𝑧 = 𝑞 𝑣𝑖𝑧/𝑇 = −7,6 𝐽. 𝐾−1
Δ𝑆 𝑇𝑜𝑡 = Δ𝑆 + Δ𝑆 𝑣𝑖𝑧 = 0
b) Irrev.: 𝑤 = 0 e Δ𝑈 = 0; 𝑞 = 0.
𝑞 𝑣𝑖𝑧 = 0 = 𝑆 𝑣𝑖𝑧
Δ𝑆 𝑇𝑜𝑡 = +7,6 𝐽. 𝐾−1

12. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones

13. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones
to be continued...

14. ENERGIA LIVRE DE GIBBS (G)
Determina a composição no equilíbrio.
Como saber se uma reação é ou não espontânea?
Resp.: Calcula-se a entropia total.
Δ𝑆Total = Δ𝑆sistema + Δ𝑆vizinhança
Análise direta da espontaneidade da reação.
Quantidade de trabalho (exceto de expansão)
envolvido.

15. Δ𝐺 = −𝑇Δ𝑆 𝑇𝑜𝑡; (𝑇, 𝑃 = 𝑐𝑡𝑒𝑠)
ENERGIA LIVRE DE GIBBS (G)
Seja Δ𝑆 𝑇𝑜𝑡 = Δ𝑆 + Δ𝑆 𝑣𝑖𝑧
Se 𝑇, 𝑃 = 𝑐𝑡𝑒𝑠 ⟶ Δ𝑆 𝑣𝑖𝑧 = − Δ𝐻/𝑇
Δ𝑆 𝑇𝑜𝑡 = Δ𝑆 −
Δ𝐻
𝑇
; (𝑇, 𝑃 = 𝑐𝑡𝑒𝑠)
Definindo:
𝐺 = 𝐻 − 𝑇𝑆
𝐺 é função de estado e 𝑇 = 𝑐𝑡𝑒;
Δ𝐺 = Δ𝐻 − 𝑇Δ𝑆
Δ𝐺
𝑇
=
Δ𝐻
𝑇
− Δ𝑆
Se 𝑃 = 𝑐𝑡𝑒 também

16. Condição de Equilíbrio:
Δ𝐺 = 0; (𝑇, 𝑃 = 𝑐𝑡𝑒𝑠)
Δ𝐺 = Δ𝐻 − 𝑇Δ𝑆

17. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones
Calcule a variação de energia livre molar, Δ𝐺 𝑚,
do processo 𝐻2 𝑂(𝑠) → 𝐻2 𝑂(𝑙) em 1 𝑎𝑡𝑚 e (a) 10℃,
(b) 0℃. Verifique, para cada temperatura, se a
fusão é espontânea, em pressão constante.
Trate Δ𝐻𝑓𝑢𝑠 = 6,01 𝑘𝐽. 𝑚𝑜𝑙−1 e Δ𝑆𝑓𝑢𝑠 = 22,0 𝐽. 𝐾−1
como independentes da temperatura.
a) Δ𝐺 𝑚 = Δ𝐻 𝑚 − 𝑇Δ𝑆 𝑚 = −0,22 𝑘𝐽. 𝑚𝑜𝑙−1
Em 10℃, a fusão é espontânea.
b) Δ𝐺 𝑚 = Δ𝐻 𝑚 − 𝑇Δ𝑆 𝑚 = 0
E 0℃, água e gelo estão em equilíbrio.

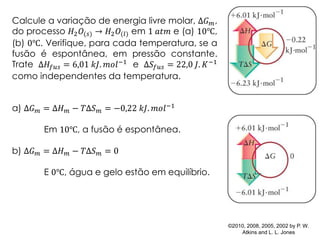
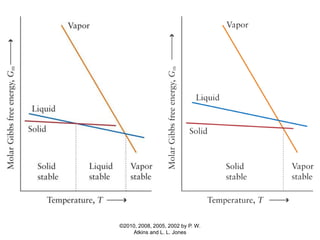
18. Calcule a variação de energia livre de Gibbs molar do processo
𝐻2 𝑂(𝑙) → 𝐻2 𝑂(𝑔) em 1 𝑎𝑡𝑚 e (a) 95℃, (b) 105℃. A entalpia de
vaporização (Δ𝐻𝑣𝑎𝑝) é 40,7 𝑘𝐽. 𝑚𝑜𝑙−1 e a entropia de vaporização
( Δ𝑆 𝑣𝑎𝑝 ) é +109,1 𝐽. 𝐾−1
. 𝑚𝑜𝑙−1
. Indique, em cada caso, se a
vaporização é espontânea ou não.
[Resp.: (a) Δ𝐺 𝑚 = +0,6 𝑘𝐽. 𝑚𝑜𝑙−1 , não espontânea; (b) Δ𝐺 𝑚 =
− 0,5 𝑘𝐽. 𝑚𝑜𝑙−1, espontânea]
Calcule a variação de energia livre de Gibbs molar do processo
𝐻𝑔(𝑙) → 𝐻𝑔(𝑔) em 1 𝑎𝑡𝑚 e (a) 350℃, (b) 370℃. A entalpia de
vaporização (Δ𝐻𝑣𝑎𝑝) é 59,3 𝑘𝐽. 𝑚𝑜𝑙−1
e a entropia de vaporização
( Δ𝑆 𝑣𝑎𝑝 ) é 94,2 𝐽. 𝐾−1. 𝑚𝑜𝑙−1 . Indique, em cada caso, se a
vaporização é espontânea ou não.

19. ©2010, 2008, 2005, 2002 by P. W.
Atkins and L. L. Jones

20. ENERGIA LIVRE DE GIBBS
(PADRÃO) DA REAÇÃO
Δ𝐺𝑓
𝑜
𝐻𝐼, 𝑔 = +1,70 𝑘𝐽. 𝑚𝑜𝑙−1
;
1
2
𝐻2(𝑔) +
1
2
𝐼2(𝑠) ⟶
1
2
𝐻𝐼(𝑔)
Δ𝐺 = ∑𝑛𝐺m produtos − ∑𝑛𝐺m(reagentes)
Se prod. e reag. no estado padrão (forma pura a 1 𝑏𝑎𝑟):
Δ𝐺 = ∑𝑛𝐺m
𝑜 produtos − ∑𝑛𝐺m
𝑜 reagentes
Δ𝐺 é fixo para uma dada temperatura.
Δ𝐺 só depende da composição da mistura de reação,
portanto, varia (pode trocar de sinal) durante a reação.
Δ𝐺𝑓
𝑜
(𝐻2, 𝑔) = Δ𝐺𝑓
𝑜
(𝐼2, 𝑠) = 0

22. Calcule a energia livre padrão de formação do
𝐻𝐼(𝑔) em 25℃ usando sua entropia padrão e sua
entalpia padrão de formação.
½ 𝐻2(𝑔) + ½ 𝐼2(𝑠) → 𝐻𝐼(𝑔)
Δ𝐻 𝑜
= 1 𝑚𝑜𝑙 × Δ𝐻𝑓
𝑜
(𝐻𝐼, 𝑔) = +26,48 𝑘𝐽
Δ𝑆 𝑜 = 𝑆 𝑚
𝑜 𝐻𝐼, 𝑔 −
1
2
𝑆 𝑚
𝑜 𝐻2, 𝑔 +
1
2
𝑆 𝑚
𝑜 𝐼2, 𝑠
Δ𝑆 𝑜 = 206,6 −
1
2
× 130,7 +
1
2
× 116,1
Δ𝑆 𝑜
= +0,0832 𝑘𝐽. 𝑚𝑜𝑙−1
Δ𝐺 𝑜 = Δ𝐻 𝑜 − 𝑇Δ𝑆 𝑜 = +1,69 𝑘𝐽

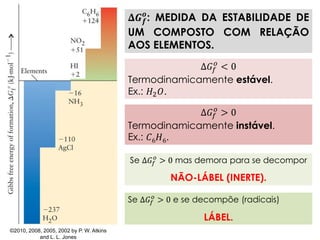
23. Calcule a energia livre padrão de formação de 𝑁𝐻3(𝑔) em 25℃,
usando a entalpia de formação e as entropias molares das
espécies envolvidas em sua formação.
[Resposta: −16,6 𝑘𝐽. 𝑚𝑜𝑙−1]
Calcule a energia livre padrão de formação do 𝐶3 𝐻6(𝑔)
, ciclo
propano, em 25℃.

24. ©2010, 2008, 2005, 2002 by P. W. Atkins
and L. L. Jones
Se Δ𝐺𝑓
𝑜
> 0 e se decompõe (radicais)
LÁBEL.
𝚫𝑮 𝒇
𝒐
: MEDIDA DA ESTABILIDADE DE
UM COMPOSTO COM RELAÇÃO
AOS ELEMENTOS.
Δ𝐺𝑓
𝑜
< 0
Termodinamicamente estável.
Ex.: 𝐻2 𝑂.
Δ𝐺𝑓
𝑜
> 0
Termodinamicamente instável.
Ex.: 𝐶6 𝐻6.
Se Δ𝐺𝑓
𝑜
> 0 mas demora para se decompor
NÃO-LÁBEL (INERTE).

25. Calcule a energia livre de Gibbs padrão da reação
4𝑁𝐻3(𝑔) + 5𝑂2(𝑔) ⟶ 4𝑁𝑂 𝑔 + 6𝐻2 𝑂(𝑔)
e decida se a reação é espontânea em condições
padrão em 25℃.
Calcule a energia livre de Gibbs padrão da reação
2𝐶𝑂(𝑔) + 𝑂2(𝑔) ⟶ 2𝐶𝑂2 𝑔
e decida se a reação é espontânea em condições
padrão em 25℃.
[Resp.: ΔGo = −514,38 kJ]
Calcule a energia livre de Gibbs padrão da reação
6𝐶𝑂2(𝑔) + 6𝐻2 𝑂(𝑙) ⟶ 𝐶6 𝐻12 𝑂6 𝑠,𝑔𝑙𝑖𝑐𝑜𝑠𝑒
+ 6𝑂2(𝑔)
e decida se a reação é espontânea em condições
padrão em 25℃.

26. 𝐶6 𝐻12 𝑂6(𝑠) + 6 𝑂2(𝑔) ⟶ 6 𝐶𝑂2 𝑔 + 6 𝐻2 𝑂 𝑙 Δ𝐺 𝑜 = −2879 𝑘𝐽;
Cada mol ligações peptídicas consome 17 kJ.
180 g de glicose  170 mols de ligações (1 glicose = 170 lig.)
Na prática somente 10; proteína possui centenas.
TRABALHO DE NÃO-EXPANSÃO
Porque energia LIVRE de Gibbs?
R.: Por que permite prever o trabalho máximo de não-
expansão (𝑤𝑒,𝑚𝑎𝑥) que um processo pode realizar a 𝑇 e
𝑃 constantes.
𝑤𝑒 (𝑒 = 𝑒𝑥𝑡𝑟𝑎) é qualquer trabalho exceto aquele de
expansão, tais como elétrico, mecânico ou bioquímico
por exemplo.

27. 𝑑𝐺 = 𝑑𝑤e,max ⇒ Δ𝐺 = 𝑤e,max ; (𝑇, 𝑃 = 𝑐𝑡𝑒𝑠)
TRABALHO DE NÃO-EXPANSÃO
𝑑𝐺 = 𝑑𝐻 − 𝑇𝑑𝑆 (𝑇 = 𝑐𝑡𝑒) mas 𝑑𝐻 = 𝑑𝑈 + 𝑃𝑑𝑉 (𝑃 = 𝑐𝑡𝑒)
daí: 𝑑𝐺 = 𝑑𝑈 + 𝑃𝑑𝑉 − 𝑇𝑑𝑆 𝑇, 𝑃 = 𝑐𝑡𝑒𝑠
como 𝑑𝑈 = 𝑑𝑤 + 𝑑𝑞 para variações infinitesimais:
𝑑𝐺 = 𝑑𝑤 + 𝑑𝑞 + 𝑃𝑑𝑉 − 𝑇𝑑𝑆
ou 𝑑𝐺 = 𝑑𝑤rev + 𝑑𝑞rev + 𝑃𝑑𝑉 − 𝑇𝑑𝑆
como 𝑑𝑆 =
𝑑𝑞rev
𝑇
𝑑𝐺 = 𝑑𝑤rev + 𝑃𝑑𝑉 e 𝑑𝑤rev = 𝑑𝑤rev,e + 𝑑𝑤rev,exp
como 𝑑𝑤rev,exp = −𝑃ext 𝑑𝑉

28. EFEITO DA TEMPERATURA

29. EFEITO DA TEMPERATURA

30. Estime a temperatura em que é
termodinamicamente possível para o carbono
reduzir óxido de ferro(III) até ferro, em condições
padrão, pela reação endotérmica:
2 𝐹𝑒2 𝑂3(𝑠) + 3 𝐶(𝑠) → 4 𝐹𝑒(𝑠) + 3 𝐶𝑂2(𝑔)
Reação endotérmica: Δ𝐻 > 0
Produção de gás: Δ𝑆 > 0
Em baixas temperaturas: Δ𝐺 𝑜
= Δ𝐻 𝑜
− 𝑇Δ𝑆 𝑜
≈ Δ𝐻 𝑜
Se 𝑇 > Δ𝐻 𝑜
/Δ𝑆 𝑜
então Δ𝐺 𝑜
< 0
Δ𝐻 𝑜 = 3 −393,5 − 2 −828,2 = +467,9 𝑘𝐽
Δ𝑆 𝑜
= 4 27,3 + 3 213,7 − 2 87,4 + 3 5,7
Δ𝑆 𝑜 = +558,4 𝐽. 𝐾−1
𝑇 =
Δ𝐻 𝑜
Δ𝑆 𝑜
= 838 K