1. O documento apresenta uma revisão de álgebra linear com foco em matrizes, incluindo operações como transposição, soma, determinante, inversa e sistemas de equações lineares.
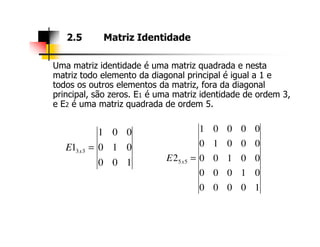
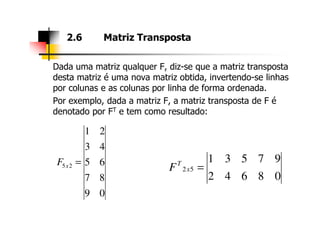
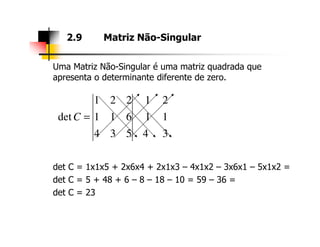
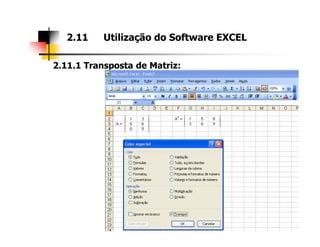
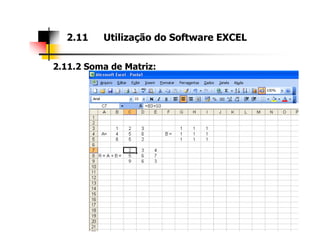
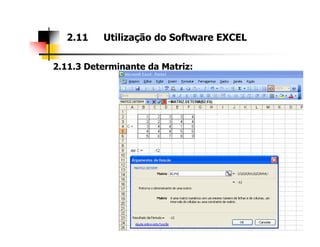
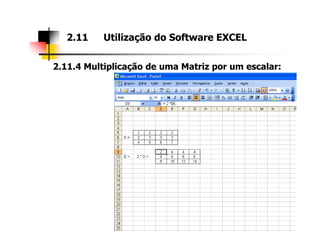
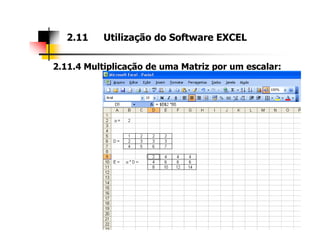
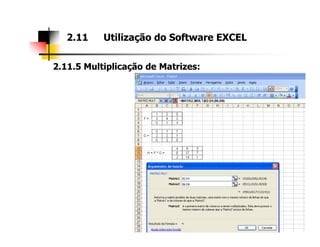
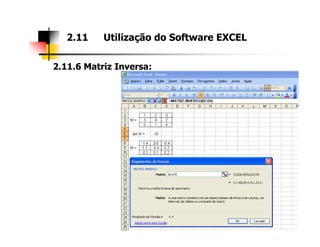
2. As seções abordam diferentes tipos de matrizes, suas propriedades e como realizar operações com elas utilizando a ferramenta Excel.
3. O objetivo é revisar conceitos de matrizes que serão úteis na resolução de problemas de programação linear usando o algoritmo Simplex.