O documento define e explica funções polinomiais, incluindo sua forma geral, exemplos, comportamento para valores extremos de x, raízes, divisão longa de polinômios e teoremas sobre restos e fatoração.

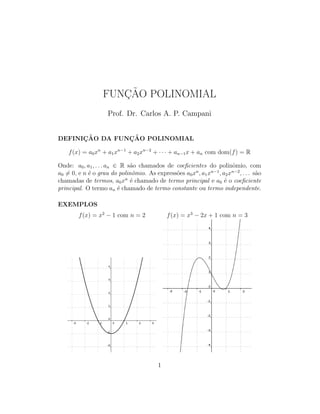
1. FUNC¸ ˜AO POLINOMIAL
Prof. Dr. Carlos A. P. Campani
DEFINIC¸ ˜AO DA FUNC¸ ˜AO POLINOMIAL
f(x) = a0xn
+ a1xn−1
+ a2xn−2
+ · · · + an−1x + an com dom(f) = R
Onde: a0, a1, . . . an ∈ R s˜ao chamados de coeficientes do polinˆomio, com
a0 = 0, e n ´e o grau do polinˆomio. As express˜oes a0xn
, a1xn−1
, a2xn−2
, . . . s˜ao
chamadas de termos, a0xn
´e chamado de termo principal e a0 ´e o coeficiente
principal. O termo an ´e chamado de termo constante ou termo independente.
EXEMPLOS
f(x) = x2
− 1 com n = 2 f(x) = x3
− 2x + 1 com n = 3
1

2. COMPORTAMENTO NOS EXTREMOS DO EIXO X
O comportamento da fun¸c˜ao polinomial para x → −∞ e x → +∞ ´e
totalmente determinado pelo seu termo principal.
Exemplo:
f(x) = x3
f(x) = x3
− 2x + 1
Vejamos isso nos seguintes gr´aficos que est˜ao em escalas progressivamente
maiores:
Escala 1 Escala 2 Escala 3
Isso significa que para valores muito grandes de x, tanto positivos quanto
negativos, x3
− 2x + 1 se aproxima de x3
, x3
− 2x + 1 ≈ x3
, ou seja:
lim
x→±∞
(x3
− 2x + 1) ≈ lim
x→±∞
x3
Os termos de menor grau s˜ao “absorvidos” pelo de maior grau, para
valores grandes de x, porque o de maior grau cresce muito mais r´apido.
2

3. A determina¸c˜ao dos limites para x → −∞ e x → +∞ pode ser resolvida
pela an´alise do grau n do polinˆomio e pelo sinal do coeficiente principal a0:
a0 > 0 e n ´ımpar a0 < 0 e n ´ımpar
limx→+∞ f(x) = +∞ limx→+∞ f(x) = −∞
limx→−∞ f(x) = −∞ limx→−∞ f(x) = +∞
a0 > 0 e n par a0 < 0 e n par
limx→+∞ f(x) = +∞ limx→+∞ f(x) = −∞
limx→−∞ f(x) = +∞ limx→−∞ f(x) = −∞
RA´IZES DAS FUNC¸ ˜OES POLINOMIAIS
As ra´ızes ou zeros da fun¸c˜ao polinomial correspondem aos pontos em que
a curva da fun¸c˜ao intercepta o eixo x.
3

4. Exemplo:
f(x) = x3
− x2
− 6x
Resolvendo a equa¸c˜ao f(x) = 0 ou x3
− x2
− 6x = 0:
1. x3
− x2
− 6x = 0
2. x(x2
− x − 6) = 0
3. x(x − 3)(x + 2) = 0 [pois as ra´ızes de x2
− x − 6 s˜ao x = 3 e x = −2]
4. x = 0 ∨ x = 3 ∨ x = −2
Assim, as ra´ızes de f s˜ao 0, 3 e −2.
A determina¸c˜ao dos zeros da fun¸c˜ao foi feita por fatora¸c˜ao do polinˆomio,
onde cada fator (x − k) determina uma raiz x = k.
Tomemos como exemplo a fun¸c˜ao f(x) = x3
− x2
− 5x − 3, que pode ser
fatorada como f(x) = (x − 3)(x + 1)2
, onde as ra´ızes s˜ao x = 3 e x = −1, e
a segunda ra´ız ´e repetida, ou seja, ´e uma raiz com duplicidade.
4

5. DIVIS˜AO LONGA DE POLINˆOMIOS
Usamos, para a divis˜ao de polinˆomios, o mesmo sistema usado com n´ume-
ros. Na divis˜ao, os n´umeros s˜ao analisados do d´ıgito mais significativo para
o menos.
Exemplo: 6696 ÷ 31
6696 ÷ 31
−62 2
49
−31 21
186
−186 216
0
Logo, 6696 ÷ 31 = 216 com resto zero (divis˜ao exata).
Sejam os polinˆomios d(x), q(x), r(x) e f(x). Podemos escrever
f(x) = d(x) × q(x) + r(x)
Ou seja:
f(x)
d(x)
= q(x) +
r(x)
d(x)
Onde:
• f(x) - dividendo
• d(x) - divisor
• q(x) - quociente
• r(x) - resto
Se r(x) = 0 ent˜ao se diz que a divis˜ao ´e exata.
Da mesma forma que com os n´umeros, posto na forma canˆonica, o po-
linˆomio ser´a dividido, na divis˜ao longa, do termo de maior grau para o de
menor grau.
5

6. Exemplo: (x3
+ 4x2
+ 2x − 1) ÷ (x + 1)
x3
+ 4x2
+ 2x − 1 ÷ x + 1
−x3
− x2
x2
0 + 3x2
+ 2x
−3x2
− 3x x2
+ 3x
0 − x − 1
x + 1 x2
+ 3x − 1
0
DISPOSITIVO DE BRIOT-RUFFINI
Suponha um polinˆomio p(x). Queremos dividir p(x) por (x − k), para
k ∈ R.
k coeficientes do dividendo termo constante do dividendo
coeficientes do quociente resto da divis˜ao
Exemplo: (x2
+ 4x + 3) ÷ (x + 1)
−1
!!
00
1
4 3
1 −1 + 4 = 3
−3 + 3 = 0
1 × (−1) = −1
55
3 0
3 × (−1) = −3
;;
Ao dividir um polinˆomio de grau n por um de grau m, o grau do polinˆomio
resultante ´e n − m. Assim, para o caso do exemplo, 2 − 1 = 1 e o resultado
ser´a um polinˆomio do 1o
grau:
(x2
+ 4x + 3) ÷ (x + 1) = (x + 3) com resto zero (divis˜ao exata)
6

7. TEOREMA DO RESTO
Se um polinˆomio f(x) ´e dividido por x − k, ent˜ao o resto ´e r = f(k).
Exemplo: Tomando o polinˆomio f(x) = x3
+ 4x2
+ 2x − 1, que ´e divis´ıvel
por x + 1, como j´a vimos, ent˜ao k = −1 e:
f(−1) = (−1)3
+ 4(−1)2
+ 2(−1) − 1 = 0
Exemplo: Seja o polinˆomio f(x) = x3
− 2x + 5 que, ao ser dividido por
d(x) = x + 1, resulta em q(x) = x2
− x − 1 com resto r(x) = 6. Basta ver
pelo teorema que f(−1) = (−1)3
− 2(−1) + 5 = 6.
TEOREMA DE D’ALEMBERT
Uma fun¸c˜ao polinomial f(x) tem um fator x − k se e somente se f(k) = 0.
APLICAC¸ ˜AO DOS TEOREMAS EM FATORAC¸ ˜AO
Exemplo: Fatorar f(x) = 3x2
+ 7x − 20.
Determinamos se f(x) ´e divis´ıvel por:
• x − 2 : r = f(2) = 3(2)2
+ 7(2) − 20 = 6 e portanto a divis˜ao n˜ao ´e
exata.
• x + 1 : r = f(−1) = 3(−1)2
+ 7(−1) − 20 = −24 e portanto a divis˜ao
n˜ao ´e exata.
• x + 4 : r = f(−4) = 3(−4)2
+ 7(−4) − 20 = 0 e portanto o polinˆomio
´e divis´ıvel por x + 4.
7

8. Efetuando a divis˜ao (3x2
+ 7x − 20) ÷ (x + 4) por Briot-Ruffini:
−4 3 7 −20
3 −12 + 7 = −5 −20 + 20 = 0
3 × (−4) = −12 −5 0
(−5) × (−4) = 20
Logo,
(3x2
+ 7x − 20) ÷ (x + 4) = 3x − 5 com r(x) = 0
8