D. triangular e critérios de congruência de triângulos
•Transferir como PPT, PDF•
1 gostou•2,467 visualizações
1) Não é possível formar um triângulo com 3 segmentos de comprimentos quaisquer. 2) Ana não pode formar um triângulo com suas 3 palhinhas de comprimentos 8cm, 4cm e 13cm. 3) Dois triângulos são congruentes se tiverem 3 lados ou 2 lados mais o ângulo entre eles ou 1 lado e os 2 ângulos adjacentes iguais.
Denunciar
Compartilhar
Denunciar
Compartilhar
Recomendados
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
Relação entre perímetros e áreas em triângulos semelhantes

Relação entre perímetros e áreas em triângulos semelhantes
Exercícios determinantes pronomes e quantificadores

Exercícios determinantes pronomes e quantificadores
Semelhante a D. triangular e critérios de congruência de triângulos
Semelhante a D. triangular e critérios de congruência de triângulos (20)
Aula 05 - Segmentos Proporcionais, Teorema de Tales e Triângulos - Semelhança...

Aula 05 - Segmentos Proporcionais, Teorema de Tales e Triângulos - Semelhança...
Geometria plana ângulos, triângulos, quadriláteros, cálculo de áreas

Geometria plana ângulos, triângulos, quadriláteros, cálculo de áreas
Mais de aldaalves
Mais de aldaalves (20)
Último
Último (20)
Projeto_de_Extensão_Agronomia_adquira_ja_(91)_98764-0830.pdf

Projeto_de_Extensão_Agronomia_adquira_ja_(91)_98764-0830.pdf
PROJETO DE EXTENSÃO I - SERVIÇOS JURÍDICOS, CARTORÁRIOS E NOTARIAIS.pdf

PROJETO DE EXTENSÃO I - SERVIÇOS JURÍDICOS, CARTORÁRIOS E NOTARIAIS.pdf
Teoria heterotrófica e autotrófica dos primeiros seres vivos..pptx

Teoria heterotrófica e autotrófica dos primeiros seres vivos..pptx
PROJETO DE EXTENSÃO I - TERAPIAS INTEGRATIVAS E COMPLEMENTARES.pdf

PROJETO DE EXTENSÃO I - TERAPIAS INTEGRATIVAS E COMPLEMENTARES.pdf
Projeto de Extensão - ENGENHARIA DE SOFTWARE - BACHARELADO.pdf

Projeto de Extensão - ENGENHARIA DE SOFTWARE - BACHARELADO.pdf
Jogo de Rimas - Para impressão em pdf a ser usado para crianças

Jogo de Rimas - Para impressão em pdf a ser usado para crianças
Seminário Biologia e desenvolvimento da matrinxa.pptx

Seminário Biologia e desenvolvimento da matrinxa.pptx
PROJETO DE EXTENÇÃO - GESTÃO DE RECURSOS HUMANOS.pdf

PROJETO DE EXTENÇÃO - GESTÃO DE RECURSOS HUMANOS.pdf
Plano de aula Nova Escola períodos simples e composto parte 1.pptx

Plano de aula Nova Escola períodos simples e composto parte 1.pptx
Estudar, para quê? Ciência, para quê? Parte 1 e Parte 2

Estudar, para quê? Ciência, para quê? Parte 1 e Parte 2
D. triangular e critérios de congruência de triângulos
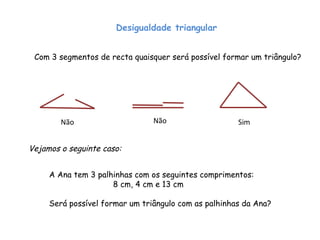
- 1. Desigualdade triangular Com 3 segmentos de recta quaisquer será possível formar um triângulo? Não Não Sim Vejamos o seguinte caso: A Ana tem 3 palhinhas com os seguintes comprimentos: 8 cm, 4 cm e 13 cm Será possível formar um triângulo com as palhinhas da Ana?
- 2. Desigualdade triangular: Num triângulo, o comprimento de qualquer lado tem de ser sempre inferior à soma do comprimento dos outros dois. a < b + c b < a+c c < a+b a b c
- 3. Construção e Congruência de triângulos Dois triângulos dizem-se geometricamente iguais se se podem sobrepor ponto por ponto, isto é, se coincidem um com o outro, quando se sobrepõem. Assim, em dois triângulos geometricamente iguais, a cada lado de um triângulo vai corresponder no outro um lado de igual medida; e a cada ângulo de um triângulo vai corresponder no outro um ângulo geometricamente igual. De um para o outro, os elementos iguais dizem-se correspondentes ou homólogos. Será que para concluirmos que dois triângulos são iguais, teremos de comparar sempre, os 3 lados de um com os 3 lados do outro e comparar sempre os 3 ângulos de um com os 3 ângulos do outro?
- 4. Critérios: 1.º Critério: l.l.l. Dois triângulos são congruentes se os três lados de um triângulo são congruentes aos três lados do outro.
- 5. 2.º Critério: l.a.l. Dois triângulos são congruentes quando têm dois lados congruentes e o ângulo por eles formado congruente.
- 6. 3.º Critério: a.l.a. Dois triângulos são congruentes se têm um lado igual e os dois ângulos adjacentes a esse lado congruentes. O símbolo significa geometricamente igual ou congruente .
