Base trigonometria 001
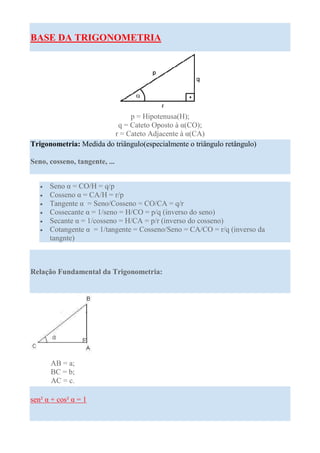
- 1. BASE DA TRIGONOMETRIA p = Hipotenusa(H); q = Cateto Oposto à α(CO); r = Cateto Adjacente à α(CA) Trigonometria: Medida do triângulo(especialmente o triângulo retângulo) Seno, cosseno, tangente, ... • Seno α = CO/H = q/p • Cosseno α = CA/H = r/p • Tangente α = Seno/Cosseno = CO/CA = q/r • Cossecante α = 1/seno = H/CO = p/q (inverso do seno) • Secante α = 1/cosseno = H/CA = p/r (inverso do cosseno) • Cotangente α = 1/tangente = Cosseno/Seno = CA/CO = r/q (inverso da tangnte) Relação Fundamental da Trigonometria: AB = a; BC = b; AC = c. sen² α + cos² α = 1
- 2. Prova : seno α = a/b => a = b.sen α cos α = c/b => c = b.cos α a² + c² = b² => b².sen²α + b².cos²α = b² => 1.sen²α + 1.cos²α = 1(corta todos os "b²") => sen²α + cos²α = 1 Ciclo trigonométrico O ciclo mostra o seno, o cosseno e a yangente no plano cartesiano. O eixo das abiscissas é o cosseno e o eixo das ordenadas é o seno e ainda tem o eixo tangencial à circunferência que é a tangente. O eixo é dividido em quadrantes I - 1° quadrante II - 2° quadrante III - 3° quadrante IV - 4° quadrante Em I, o seno, o cosseno e a tangente são positivos; Em II, o seno é positivo; Em III, a tangente é positiva; Em IV, o cosseno é positivo. O ciclo trigonométrico é unitário, ou seja, do centro à circunferência é 1, porque o maior seno e maior cosseno é igual à 1 e o menor seno e menor cosseno é igual à -1.
- 3. Principais senos, cossenos e tangentes Arco Duplo • sen(A + B) = senA.cosB + senB.cosA (Vídeo provando esta fórmula: Provando sen(a + b)) • sen(A - B) = senA.cosB - senB.cosA • cos(A + B) = cosA.cosB - senA.senB • cos(A - B) = cosA.cosB + senA.senB • sen 2A = sen(A + A) = senA.cosA + senA.cosA = 2senA.cosA • cos 2A = cos(A + A) = cosA.cosA - senA.senA = cos²A - sen²A • cos 2A = cos²A - sen²A = cos²A - (1 - cos²A)Relação fundamental = cos²A - 1 + cos²A = 2cos²A - 1 • cos 2A = cos² A - sen² A = (1 - sen²A) - sen²A = 1 - 2sen²A
- 4. IIIIIIIIIIIIIIIIIIIIIIIQUESTÕESIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 01 - (Fuvest - modificada)Se α é um ângulo tal que 0 < α < π/2 e senα = a, então tg(π - α) é igual a quanto? α é menor que 90° graus então pertence ao primeiro quadrante. π é 180° então π - α está entre 90° e 180°, ou seja, segundo quadrante(figura). Como tangente é seno sobre cosseno e o seno de α é "a", a resposta terá um "a" em cima. Como a tangente no segundo quadrante é negativa, a resposta será negativa. Esta não é a figura da questão, então desconsiderem que o α seja o ângulo mostrado. Imaginem o ângulo mostrado como (π - α) O ângulo que a figura mostra pode ser π - α. A reta que sai do ponto "A" marca o cosseno na reta x. Podemos chamar o cosseno de "m", por exemplo. sen²α + cos² α = 1 a² + m² = 1 m² = 1 - a² m = √1 - a² tangente = seno/cosseno = a/m = a/√1 - a² = -a/√1 - a² Resposta: -a . √1 - a²
- 5. 02 - Considere a igualdade tgx = cotgx + [P.(2 - sec²x)/2tgx]. Qual é o valor de P, para o qual a igualdade acima seja válida para todo x R, x ≠ 0 kπ/2, K inteiro. tgx = cotgx + [P.(2 - sec²x)/2tgx] tgx - cotgx = 2.P - sec²x.P 2tgx tgx.2tgx - 1 .2tgx = 2.P - sec²x.P tgx 2tg²x - 2 = 2.P - sec²x.P 2. sen²x - 2 = 2.P - 1 .P cos²x cos²x 2.sen²x - 2cos²x = 2cos²x.P - P cos²x 2(sen²x - cos²x) = P(2cos²x - 1) 2(sen²x - cos²x) = P(cos²x + cos²x - 1) sen²α + cos²α = 1 => cos²α - 1 = -sen²α 2(sen²x - cos²x) = P(cos²x - sen²x) P = 2 (sen²x - cos²x) -1(sen²x - cos²x) Resposta: P = -2 03 - Para representar os harmônicos emitidos pelos sons dos instrumenteos da orquestra, usam-se funções trigonométricas. A expressão 2 sen²x + 2cos²x - 5 envolve estas funções e, para π < x < 3π/2, seu valor é: 2sen²x + 2cos²x - 5 = 2(sen²x + cos²x) - 5 = 2.1 - 5 = 2-5= -3 Resposta: -3
- 6. 04 - Demonstre a identidade a seguir: tg x + cotg x = sec x . cossec x sen + cos = 1 . 1 cos sen cos sen sen² + cos² = 1 sen.cos sen.cos 1 = 1 sen.cos sen.cos sen.cos = 1 sen.cos 1=1 05 - Quanto é sen75°? sen75° = sen (30 + 45) = sen30.cos45 + sen45.cos30 1 . √2 + √2 . √3 2 2 2 2 √2 + √6 4 4 √2 + √6 4 Resposta: √2 + √6 4 06 - Obtenha todos os pares (x, y) com x, y ∈ [0, 2π], tais que: sen(x + y) + sen(x - y) = 1/2 sen x + cos y = 1 sen (x + y) = sen x . cos y + sen y . cos x sen (x - y) = sen x . cos y - sen y . cos x sen x . cos y + sen y . cos x + sen x . cos y - sen y . cos x = 1/2 sen x . cos y + sen y . cos x + sen x . cos y - sen y . cos x = 1/2 2 sen x . cos y = 1/2 sen x . cos y = 1/4 sen x + cos y = 1 sen x . cos y = 1/4 sen x = 1/2 = 30° cos y = 1/2 = 60° Resposta: (30°, 60°); (390°, 420°); ...
- 7. 07 - Se a medida de um arco, em graus, é igual a 128, sua medida em radianos é igual a: a) (π/4) - 17 Essa questão é super simples! b) (54/15)π É só fazer uma regra de três: c) (64/45)π d) (16/25)π 180 ----> π e) (32/45)π 128 ----> x 180 . x = π . 128 x = π . 128/180 x = (32/45)π Resposta: e) (32/45)π 08 - A tangente do ângulo 2x é dada em função da tangente de x pela seguinte fórmula: tg 2x = 2tg x/1 - tg²x Calcule um valor aproximado da tangente do ângulo 22º 30'. a) 0,22 b) 0,41 c) 0,50 Considere 22° 30' = x d) 0,72 Portanto, 2x = 45° e) 1,00 tg 2x = 2tg x/1 - tg²x tg 45° = 2 . tg 22° 30'/1 - tg² 22° 30' tg 22° 30' = - 1 + √8/2 1 = 2 . tg 22° 30'/1 - tg² 22° 30' √8 é aproximadamente 2,82/2 = 1,41 0 = (2 . tg 22° 30'/1 - tg² 22° 30') - 1 1,41 - 1 = 0,41 = tg 22° 30' 0 = 2 . tg 22° 30' - 1 + tg² 22° 30' tg² 22° 30' + 2 . tg 22° 30' - 1 = 0 --> Eq. Resposta: b)0,41 2° Grau tg 22° 30' = x x² + 2x - 1 = 0 / = 4 + 4 / = 8 x = - 2 +- √8 2 x' = -1 + √8 2 x'' = - 1 - √8 ---> tg 22° 30' é positiva 2
- 8. 09 - O desenvolvimento de 1 - tg² x para x ≠ nπ ± π/2, sendo n um inteiro qualquer é: 1 + tg² x a) sec² x - 1 b) sec² x + 1 c) sen² x - cos² x d) cos² x - sen² x e) tg² x 1 - sen² x cos² x 1 + sen² x cos² x cos² x - sen² x cos² x cos² x + sen² x cos² x cos² x - sen² x sen² x + cos² x = 1 cos² x - sen² x Resposta: d) cos² x - sen² x 10 - Qual o valor da expressão abaixo? (2 . sen4 20° - 2 . cos4 20°) . cossesc4 20° 3 - 3 . cotg4 20° a) - 2/3 b) 2/3 c) 1/3 d) - 1/3 e) 0 (2 . sen4 20° - 2 . cos4 20°) . 1/sen4 20° 3 sen4 - 3 cos4 20° sen4 20° 2 . sen4 20° - 2 . cos420° 3 sen4 20° - 3 cos4 20° 2 . (sen4 20° - cos420°) 3. (sen4 20° - cos4 20°) 2/3 Resposta: b)2/3
