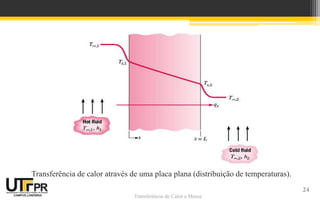
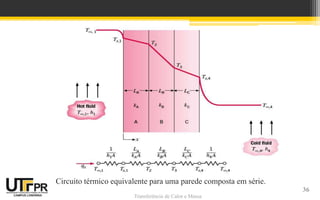
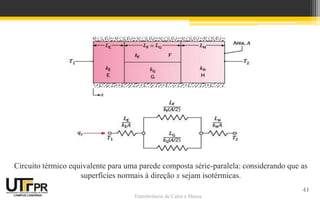
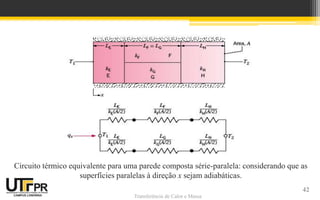
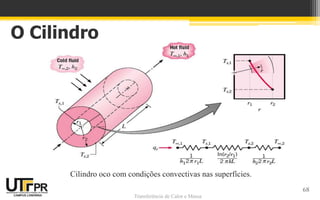
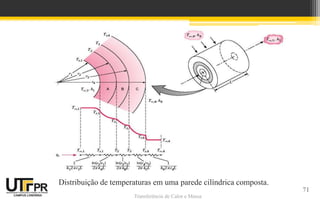
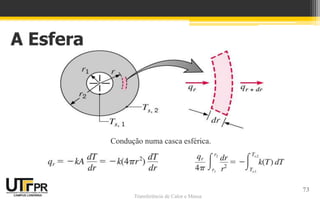
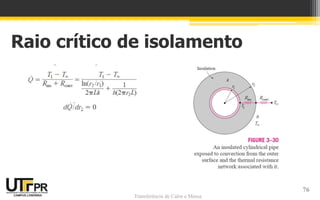
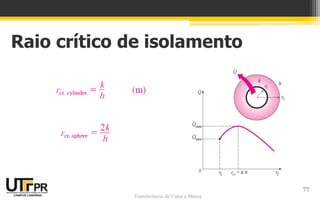
1. Transferência de Calor e
Massa
Prof. Dr. Lucas Freitas Berti
Engenharia de Materiais - UTFPR
lenberti@gmail.com
1

2. Aula 4
Condução Unidimensional em
Regime Permanente
29/05/2013

3. Transferência de Calor e Massa
Presença
Cobrança da presença
3

4. Transferência de Calor e Massa
Revisão
 A Equação da Difusão de Calor (Difusão Térmica)
 Condições de Contorno e Inicial
4
 Ementa

5. Transferência de Calor e Massa
A Equação da
Difusão de Calor
(Difusão Térmica)
5

6. Transferência de Calor e Massa
Um dos objetivos principais da análise da condução
de calor é determinar o campo de temperaturas
(distribuição de temperaturas) num meio resultante
das condições impostas em suas fronteiras.
Uma vez conhecida esta distribuição, o fluxo de
calor por condução em qualquer ponto do meio ou na
sua superfície pode ser determinado através da Lei de
Fourier.
6

7. Transferência de Calor e Massa
Objetivo: uma equação diferencial cuja solução, para
condições de contorno especificadas, forneça a
distribuição de temperaturas no meio.
Metodologia: aplicação da conservação da energia, ou
seja, define-se um volume de controle diferencial,
identificam-se os processos de transferência de
energia relevantes e substituem-se as equações das
taxas de transferência de calor apropriadas.
7

8. Transferência de Calor e Massa
acusaigent EEEE  
Volume de controle diferencial, dx.dy.dz, para análise da condução em coordenadas cartesianas.
8

9. Transferência de Calor e Massa
 Equação da Difusão do Calor (Difusão Térmica)
Coordenadas cartesianas
t
T
cq
z
T
k
zy
T
k
yx
T
k
x
p

































Em qualquer ponto do meio, a taxa líquida de transferência
de energia por condução no interior de um volume unitário
somada à taxa volumétrica de geração de energia térmica deve
ser igual à taxa de variação da energia térmica acumulada no
interior deste volume.
9

10. Transferência de Calor e Massa
Com frequência, é possível trabalhar com versões
simplificadas da Equação do Calor.
Exemplo: condução 1D com propriedades constantes e
sem geração de energia.
t
T
x
T






1
2
2
10

11. Transferência de Calor e Massa
11
Transferência de Calor e Massa
Heat Flux Components
(2.22)
     
    
  
T T T
q k i k j k k
r r z
rq q zq
• Coordenadas Cilíndricas:  , ,T r z
sin
     
    
  
T T T
q k i k j k k
r r r  
(2.25)
rq q
q
•Coordenadas Esféricas  , ,T r  
• Coordenadas Cartesianas:  , ,T x y z
     
    
  
T T T
q k i k j k k
x y z
xq yq zq
(2.3)

12. Transferência de Calor e Massa
12
Transferência de Calor e Massa
Heat Flux Components (cont.)
• In angular coordinates , the temperature gradient is still
based on temperature change over a length scale and hence has
units of C/m and not C/deg.
 or ,  
• Heat rate for one-dimensional, radial conduction in a cylinder or sphere:
– Cylinder
2  r r r rq A q rLq
or,
2    r r r rq A q rq
– Sphere
2
4  r r r rq A q r q

13. Transferência de Calor e Massa
 Equação do Calor: Coordenadas Cilíndricas
t
T
cq
z
T
k
z
T
k
rr
T
kr
rr
p


































2
11
radial, r
circunferencial, Φ
axial, z
13

14. Transferência de Calor e Massa
 Equação do Calor: Coordenadas Esféricas
radial, r
polar, θ
azimutal, Φ
t
T
cq
T
senk
senr
T
k
senrr
T
kr
rr
p




































222
2
2
111
14

15. Transferência de Calor e Massa
Condições de
Contorno e Inicial
15

16. Transferência de Calor e Massa
Para determinação da distribuição de temperaturas num
meio, é necessário resolver a forma apropriada da Equação
do Calor.
Tal solução depende das condições físicas existentes nas
fronteiras do meio, e, se a situação variar com o tempo
(processo transiente), a solução também depende das
condições existentes no meio em algum instante inicial.
16

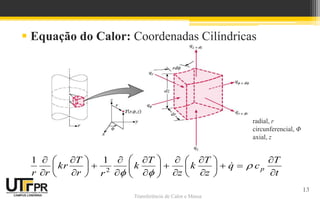
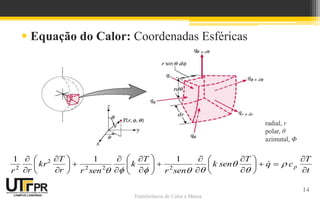
17. Transferência de Calor e Massa
Condição Inicial: como a Equação do Calor é de primeira
ordem em relação ao tempo, apenas uma condição deve ser
especificada. [T(x,t)t=0 = T(x,0)]
Condições na Fronteira (Condições de Contorno): há várias
possibilidades comuns que são expressas de maneira simples
em forma matemática. Como a Equação do Calor é de segunda
ordem em relação às coordenadas espaciais, duas condições de
contorno devem ser fornecidas para cada coordenada espacial
necessária para descrever o problema.
17

18. Transferência de Calor e Massa
Condições de contorno para a equação da difusão do calor na superfície (x = 0).
Condição de
Dirichlet
Condição de
Neumann
Condição de
Robin
18

19. Transferência de Calor e Massa
Homework
Chapter 2 (Incropera et al, 2008):
 2.2, 2.3, 2.4, 2.6, 2.8, 2.13, 2.20, 2.26, 2.35, 2.36,
2.39, 2.50
19

20. Transferência de Calor e Massa
Exemple 2.3
20

21. Transferência de Calor e Massa
Exemple 2.3
21

22. Transferência de Calor e Massa
Sumário da aula
 A Parede Plana
▫ Distribuição de Temperaturas
▫ Resistência Térmica
▫ A Parede Composta
▫ Resistência de Contato
 Uma Análise Alternativa da Condução
 Sistemas Radiais
▫ O Cilindro
▫ A Esfera
 Resumo dos Resultados da Condução 1D
22
 Ementa

23. Transferência de Calor e Massa
A Parede Plana
23

24. Transferência de Calor e Massa
Transferência de calor através de uma placa plana (distribuição de temperaturas).
24

25. Transferência de Calor e Massa
Distribuição de Temperaturas
Em regime permanente, sem a presença de fontes ou
sumidouros de energia no interior da parede, a forma
apropriada da Equação do Calor é:
0





dx
dT
k
dx
d
Para condução 1D em RP numa parede plana sem geração
de calor, o fluxo térmico é uma constante, independente de x.
25

26. Transferência de Calor e Massa
se k = cte, a equação pode ser integrada duas vezes,
obtendo-se a solução geral,
As condições de contorno para este problema são:
com isso, tem-se que
  21 cxcxT 
  10 ,sTT    2,sTLT 
L
TT
c ,s,s 12
1

 12 ,sTc 
26

27. Transferência de Calor e Massa
Substituindo na solução geral, a distribuição de
temperaturas é
    112 ,s,s,s T
L
x
TTxT 
Para a condução 1D em RP numa parede plana sem
geração de calor e condutividade térmica constante, a
temperatura varia linearmente com x.
27

28. Transferência de Calor e Massa
Utilizando a distribuição de temperaturas e a Lei de
Fourier, tem-se que
 21 ,s,sx TT
L
kA
dx
dT
kAq 
 21 ,s,s
x
x TT
L
k
A
q
q 
A taxa de transferência de calor por condução qx e o fluxo
térmico q"x são constantes, independentes de x.
28

29. Transferência de Calor e Massa
 Procedimento Padrão para solução de problemas
de condução.
1) Solução geral para a distribuição de temperaturas é obtida
através da resolução da forma apropriada da Equação do
Calor.
2) As condições de contorno são utilizadas para obtenção da
solução particular
3) Lei de Fourier é utilizada para determinação da taxa de
transferência de calor.
29

30. Transferência de Calor e Massa
Resistência Térmica
Caso especial da transferência de calor 1D sem geração
interna de energia e com propriedades constantes.
Analogia entre as difusões de calor e de carga elétrica.
Da mesma forma que uma resistência elétrica está
associada à condução de eletricidade, uma resistência
térmica está associada à condução de calor.
Definição: razão entre um potencial motriz e a
correspondente taxa de transferência.
30

31. Transferência de Calor e Massa
 Resistência térmica para condução
 Resistência térmica para convecção
kA
L
q
TT
R
x
,s,s
cond,t 

 21
hAq
TT
R s
conv,t
1


 
Representações na forma de circuitos fornecem uma
ferramenta útil tanto para a conceituação quanto para a
quantificação de problemas da transferência de calor.
31

32. Transferência de Calor e Massa
 Circuito térmico equivalente para a parede plana com
condições de convecção nas superfícies.
qx pode ser determinada pela consideração em separado de
cada elemento da rede (qx é constante ao longo da rede)























 
Ah
TT
kA
L
TT
Ah
TT
q ,,s,s,s,s,
x
2
2221
1
11
11
32

33. Transferência de Calor e Massa
Em termos da diferença de temperatura global e da
resistência térmica total, a taxa de transferência de
calor pode ser representada por
sendo que
tot
,,
x
R
TT
q 21  

AhkA
L
Ah
Rtot
21
11

33

34. Transferência de Calor e Massa
A troca radiante entre a superfície e a vizinhança pode,
também, ser importante se h for pequeno.
 Resistência térmica para radiação
Ahq
TT
R
rrad
vizs
rad,t
1



Nota: as resistências convectiva e radiante em uma superfície
atuam em paralelo, e se T∞ = Tviz, elas podem ser combinadas
para se obter uma resistência na superfície única e efetiva.
34

35. Transferência de Calor e Massa
Parede Composta
Circuito térmicos equivalentes podem ser utilizados em
sistemas mais complexos, como, por exemplo, paredes
compostas.
Tais paredes possuem uma quantidade qualquer de
resistências térmicas em série e em paralelo, devido à
presença de camadas diferentes de materiais.
35

36. Transferência de Calor e Massa
Circuito térmico equivalente para uma parede composta em série.
36

37. Transferência de Calor e Massa
A taxa de transferência de calor 1D para esse sistema
pode ser representada por
sendo que

 

t
,,
x
R
TT
q 41
 




































AhAk
L
Ak
L
Ak
L
Ah
R
C
C
B
B
A
A
t
41
11
37

38. Transferência de Calor e Massa
Alternativamente, a taxa de transferência de calor pode
ser relacionada à diferença de temperaturas e à
resistência térmica associadas a cada elemento. Por
exemplo,
























 
Ak
L
TT
Ak
L
TT
Ah
TT
q
B
B
A
A
,s,s,
x
3221
1
11
1
38

39. Transferência de Calor e Massa
Em sistemas compostos, é conveniente definir um
coeficiente global de transferência de calor, U, por
uma expressão análoga à Lei de Resfriamento de
Newton.
ou ainda,
 
UAq
T
RR ttot
1
TUAqx 
39

40. Transferência de Calor e Massa
As paredes compostas também podem ser caracterizadas
por configurações série-paralelo. Embora nesse sistema
o escoamento de calor seja multidimensional, é
razoável a hipótese de condições 1D.
Com base nesta hipótese, dois circuitos térmicos
diferentes podem ser usados.
40

41. Transferência de Calor e Massa
Circuito térmico equivalente para uma parede composta série-paralela: considerando que as
superfícies normais à direção x sejam isotérmicas.
41

42. Transferência de Calor e Massa
Circuito térmico equivalente para uma parede composta série-paralela: considerando que as
superfícies paralelas à direção x sejam adiabáticas.
42

43. Transferência de Calor e Massa
Resistência de Contato
x
BA
c,t
q
TT
R



43

44. Transferência de Calor e Massa
A existência de uma resistência de contato não-nula se
deve principalmente aos efeitos da rugosidade da
superfície.
A transferência de calor é devida à condução através da
área de contato real e à condução e/ou radiação
através dos interstícios.
Os resultados mais confiáveis para predizer R"t,c são
aqueles que foram obtidos experimentalmente.
44

45. Transferência de Calor e Massa
45

46. Transferência de Calor e Massa
Em muitas aplicações ocorre a transferência de calor
em um meio saturado, i.e. meio poroso, que é uma
combinação estacionária de fluido e um sólido.
No capítulo 7 é estudado sobre leito fluidizado, onde
um sólido estacionário é percolado por um fluido
46

47. Transferência de Calor e Massa
Meio poroso
47

48. Transferência de Calor e Massa
Meio poroso
48

49. Transferência de Calor e Massa
Meio poroso
49

50. Transferência de Calor e Massa
Meio poroso
50

51. Transferência de Calor e MassaTransferência de Calor e Massa
 Tanto keff,min e keff,max dão boas estimativas para meios
onde efeitos de micro- e nanoescala são desprezíveis.
Do contrário, a equação de Maxwell para é preferível
para melhores valores:
 No entanto, ela é aplicável para meios com no
máximo 0,25 de porosidade
51

52. Transferência de Calor e Massa
Problema 3.1
52

53. Transferência de Calor e Massa
Problema 3.1
53

54. Transferência de Calor e Massa
Problema 3.1
54

55. Transferência de Calor e Massa
Problema 3.1
55

56. Transferência de Calor e Massa
Problema 3.1
56

57. Transferência de Calor e Massa
Problema 3.1
57

58. Transferência de Calor e Massa
Problema 3.1
58

59. Transferência de Calor e Massa
Problema 3.1
59

60. Transferência de Calor e Massa
Problema 3.1
60

61. Transferência de Calor e Massa
Uma Análise
Alternativa da
Condução
61

62. Transferência de Calor e Massa
Para condições de RP, sem geração de calor e sem
perda de calor pelas superfícies laterais, a taxa de
transferência de calor qx é necessariamente uma
constante independente de x, ou seja, para qualquer
elemento diferencial dx, qx = qx+dx .
Essa condição é, obviamente, uma consequência da
exigência da conservação da energia e deve ser válida
mesmo que A(x) e k(T).
62

63. Transferência de Calor e Massa
Um procedimento alternativo pode ser utilizado para as
condições de interesse no momento.
63

64. Transferência de Calor e Massa
Além disso, mesmo que a distribuição de temperaturas
possa ser 2D, variando em função de x e y, com
frequência é razoável desprezar a variação na direção
y e supor uma distribuição 1D na direção x.
Com isso, é possível trabalhar exclusivamente com a
Lei de Fourier ao efetuar uma análise de condução.
   
dx
dT
xATkqx 
64

65. Transferência de Calor e Massa
Em particular, uma vez que a taxa condutiva é uma
constante, a equação da taxa pode ser integrada,
mesmo sem o prévio conhecimento de qx e de T(x).
 
  
x
x
T
T
x dTTk
xA
dx
q
0 0
65

66. Transferência de Calor e Massa
Sistemas Radiais
66

67. Transferência de Calor e Massa
Com frequência, em sistemas cilíndricos e esféricos há
gradientes de temperatura somente na direção radial,
o que possibilita analisá-los como sistemas 1D.
Além disso, em RP sem geração de calor, tais sistemas
podem ser analisados pelo método padrão, que
começa com a forma apropriada da Equação do
Calor, ou pelo método alternativo, que começa com
a forma apropriada da Lei de Fourier.
67

68. Transferência de Calor e Massa
O Cilindro
Cilindro oco com condições convectivas nas superfícies.
68

69. Transferência de Calor e Massa
 Distribuição de temperaturas
     
  2
21
2
21 ,s,s,s T
rrln
rrln
TTrT 
A distribuição de temperaturas associadas à condução radial
através de uma parede cilíndrica é logarítmica, não linear. (Na
parede plana sob as mesmas condições ela é linear).
69

70. Transferência de Calor e Massa
 Taxa de transferência de calor
 Resistência térmica (condução radial)
 
 12
212
rrln
TTLk
q ,s,s
r



 
Lk
rrln
R cond,t
2
12

70

71. Transferência de Calor e Massa
Distribuição de temperaturas em uma parede cilíndrica composta.
71

72. Transferência de Calor e Massa
     































 
44
342312
11
41
2
1
2222
1
LhrLk
rrln
Lk
rrln
Lk
rrln
Lhr
TT
q
CBA
,,
r

 41
41
,,
tot
,,
r TTUA
R
TT
q 




  1
44332211

 tRAUAUAUAU
 Taxa de transferência de calor
 Coeficiente global de transferência de calor
72

73. Transferência de Calor e Massa
A Esfera
Condução numa casca esférica.
73

74. Transferência de Calor e Massa
 Distribuição de temperaturas
 Taxa de transferência de calor
 Resistência térmica (condução casca esférica)
     
  1
21
1
12
1
1
,s,s,s T
rr
rr
TTrT 








 
   21
21
11
4
rr
TTk
q ,s,s
r











21
11
4
1
rrk
R cond,t

74

75. Transferência de Calor e Massa
Esferas compostas podem ser tratadas da mesma forma
que as paredes e os cilindros compostos, onde formas
apropriadas da resistência total e do coeficiente
global de transferência de calor podem ser
determinadas.
75

76. Transferência de Calor e Massa
Raio crítico de isolamento
76

77. Transferência de Calor e Massa
Raio crítico de isolamento
77

78. Transferência de Calor e Massa
Resumo dos
Resultados da
Condução 1D
78

79. Transferência de Calor e Massa
21 ,s,s TTT 
79