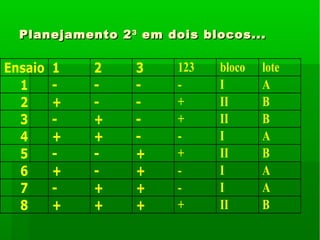
O documento descreve um planejamento fatorial completo com três fatores (temperatura, catalisador e concentração) e suas respectivas interações para analisar o rendimento de uma reação. Os principais efeitos encontrados foram da temperatura, catalisador e concentração, com interação significativa entre temperatura e concentração.

1. EAL 3012 - ESTATÍSTICA,EAL 3012 - ESTATÍSTICA,
PLANEJAMENTO EPLANEJAMENTO E
OTIMIZAÇÃO DEOTIMIZAÇÃO DE
EXPERIMENTOSEXPERIMENTOS

2. Planejamento fatorialPlanejamento fatorial
2233
 O planejamento fatorial completo tem 8O planejamento fatorial completo tem 8
experimentos.experimentos.
 Podem ser apresentados na ordem padrão. (asPodem ser apresentados na ordem padrão. (as
colunas começam com o nível (-)colunas começam com o nível (-)
 Exemplo (p105): Rendimento como função de:Exemplo (p105): Rendimento como função de:
 11 - Temperatura- Temperaturaoo
C (-) 40 e (+) 60C (-) 40 e (+) 60
 22 - Catalisador Tipo (-) A e (+) B- Catalisador Tipo (-) A e (+) B
 33 - Concentração Mol (-) 1,0 e (+) 1,5- Concentração Mol (-) 1,0 e (+) 1,5

3. Resultados de umResultados de um
planejamentoplanejamento
1 T[40;60]; 2 K[A;B]; 31 T[40;60]; 2 K[A;B]; 3
C[1;1,5]C[1;1,5]
Ensaio 1 2 3 rend % Media %
1 - - - 56 52 54,0
2 + - - 85 88 86,5
3 - + - 49 47 48,0
4 + + - 64 62 63,0
5 - - + 65 61 63,0
6 + - + 92 95 90,5
7 - + + 57 60 58,5
8 + + + 70 74 72,0

4. Planejamento fatorialPlanejamento fatorial
completo...completo...
 A partir da matriz de planejamento podemos formar aA partir da matriz de planejamento podemos formar a
tabela detabela de coeficientes de contrastecoeficientes de contraste
 Temos três fatores principais...Temos três fatores principais...
 11 Temperatura,Temperatura, 22 catalisador,catalisador, 33 concentraçãoconcentração
 Três interações de dois fatoresTrês interações de dois fatores::
 12 (Txcat), 13 (Tx conc.) e 23 (cat. X conc) e12 (Txcat), 13 (Tx conc.) e 23 (cat. X conc) e
 Uma interação de três fatoresUma interação de três fatores
 123 (T x cat. X conc).123 (T x cat. X conc).
 Os sinais de cada interação são obtidos multiplicando-Os sinais de cada interação são obtidos multiplicando-
se as colunasse as colunas

5. Coeficientes deCoeficientes de
contrastecontraste Média 1 2 3 12 13 23 123 RespMédia 1 2 3 12 13 23 123 Resp
 + - - - + + + - 54,0+ - - - + + + - 54,0
 + + - - - - + + 86,5+ + - - - - + + 86,5
 + - + - - + - + 48,0+ - + - - + - + 48,0
 + + + - + - - - 63,0+ + + - + - - - 63,0
 + - - + + - - + 63,0+ - - + + - - + 63,0
 + + - + - + - - 93,5+ + - + - + - - 93,5
 + - + + - - + - 58,5+ - + + - - + - 58,5
 + + + + + + + + 72,0+ + + + + + + + 72,0

6. Cálculo da média e dosCálculo da média e dos
efeitosefeitos
 Y méd. = 67,31Y méd. = 67,31
 Efeitos principaisEfeitos principais
T (1) = 22,88 ; Cat. (2) = -13,88; Conc (3) = 8,88T (1) = 22,88 ; Cat. (2) = -13,88; Conc (3) = 8,88
 InteraçõesInterações
 2 fatores2 fatores
 TxCat (12) = -8,63 ; TxConc. (13) =-0,88 eTxCat (12) = -8,63 ; TxConc. (13) =-0,88 e
CatxConc. (23) = 0,88CatxConc. (23) = 0,88
 3fatores Tx Cat. X Conc. (123) = -0,133fatores Tx Cat. X Conc. (123) = -0,13

7. Erro experimentalErro experimental
 Cada ensaio foi realizado 2 vezes, assimCada ensaio foi realizado 2 vezes, assim
temos a estimativa da variância com umtemos a estimativa da variância com um
grau de liberdadegrau de liberdade
∑=
−
−
==
N
i
i xx
N
sxV
1
22
)(
1
1
)(

8. Estimativa do erroEstimativa do erro
 Temos então que s2 = 5,2Temos então que s2 = 5,2
 Se os valores são independentes podemosSe os valores são independentes podemos
obter uma estimativa da variância de umobter uma estimativa da variância de um
efeito ....efeito ....
 Cada um dos oito valores do planejamentoCada um dos oito valores do planejamento
é a média de dois experimentos.é a média de dois experimentos.
 Se a variância de uma observaçãoSe a variância de uma observação
individual é estimada em 5,2 a variância daindividual é estimada em 5,2 a variância da
média de duas observações será igual amédia de duas observações será igual a
5,2/2 = 2,6;5,2/2 = 2,6;

9. Estimativa do erroEstimativa do erro
 Variância de um efeito = 2,6/2 =1,3Variância de um efeito = 2,6/2 =1,3
 O erro padrão é a raiz quadrada daO erro padrão é a raiz quadrada da
variância e logo temos que o valor évariância e logo temos que o valor é
aproximadamente 1,14%.aproximadamente 1,14%.
 O erro padrão do rendimento médio será aO erro padrão do rendimento médio será a
metade disso.... 0,57%metade disso.... 0,57%
 Obs: válido para repetições autenticas eObs: válido para repetições autenticas e
experimentos aleatorizados.experimentos aleatorizados.

10. Análise com oAnálise com o
software...software...
Effect Estimates; Var.:Var5; R-sqr=,98822; Adj:,97792 (Spreadsheet1)
2**(3-0) design; MS Residual=5,1875
DV: Var5
Effect Std.Err. t(8) p -95,%
Cnf.Limt
+95,%
Cnf.Limt
Coeff. Std.Err.
Coeff.
-95,%
Cnf.Limt
+95,%
Cnf.Lim
nterc.
2
3
4
67,3125 0,569402 118,2161 0,000000 65,9995 68,6255 67,31250 0,569402 65,99946 68,625
22,8750 1,138804 20,0869 0,000000 20,2489 25,5011 11,43750 0,569402 10,12446 12,750
-13,8750 1,138804 -12,1838 0,000002 -16,5011 -11,2489 -6,93750 0,569402 -8,25054 -5,624
8,8750 1,138804 7,7933 0,000053 6,2489 11,5011 4,43750 0,569402 3,12446 5,750
-8,6250 1,138804 -7,5737 0,000065 -11,2511 -5,9989 -4,31250 0,569402 -5,62554 -2,999
-0,8750 1,138804 -0,7683 0,464354 -3,5011 1,7511 -0,43750 0,569402 -1,75054 0,875
0,8750 1,138804 0,7683 0,464354 -1,7511 3,5011 0,43750 0,569402 -0,87554 1,750
0,1250 1,138804 0,1098 0,915300 -2,5011 2,7511 0,06250 0,569402 -1,25054 1,375

11. Efeitos calculadosEfeitos calculados
 Média 67,3± 0,57Média 67,3± 0,57
 TemperaturaTemperatura (1) = 22,9±1,14(1) = 22,9±1,14
 CatalisadorCatalisador (2) = -13,9±1,14(2) = -13,9±1,14
 ConcentraçãoConcentração (3) = 8,9±1,14(3) = 8,9±1,14
 Interações:Interações:
 (12) = -8,6±1,14(12) = -8,6±1,14 ; (13) = -0,9±1,14; (13) = -0,9±1,14
 (23) = 0,9±1,14(23) = 0,9±1,14
 (123) = 0,1±1,14(123) = 0,1±1,14

12. Gráfico de Pareto...Gráfico de Pareto...
P a r e t o C h a r t o f S t a n d a r d i z e d E f f e c t s ; V a r i a b l e : V a r 5
2 * * ( 3 - 0 ) d e s i g n ; M S R e s i d u a l = 5 , 1 8 7 5
D V : V a r 5
, 1 0 9 7 6 4 3
, 7 6 8 3 4 9 8
- , 7 6 8 3 5
- 7 , 5 7 3 7 3
7 , 7 9 3 2 6 2
- 1 2 , 1 8 3 8
2 0 , 0 8 6 8 6
p = , 0 5
S t a n d a r d i z e d E f f e c t E s t i m a t e ( A b s o l u t e V a l u e )
1 * 2 * 3
2 b y 3
1 b y 3
1 b y 2
( 3 ) V a r 4
( 2 ) V a r 3
( 1 ) V a r 2

13. Gráfico normal de probabilidadeGráfico normal de probabilidade
P r o b a b i l i t y P l o t ; V a r . : V a r 5 ; R - s q r = , 9 8 8 2 2 ; A d j : , 9 7 7 9 2
2 * * ( 3 - 0 ) d e s i g n ; M S R e s i d u a l = 5 , 1 8 7 5
D V : V a r 5
( 2 ) V a r 3
1 b y 2
1 b y 3
1 * 2 * 3
2 b y 3
( 3 ) V a r 4
( 1 ) V a r 2
- 2 0 - 1 5 - 1 0 - 5 0 5 1 0 1 5 2 0 2 5
- I n t e r a c t i o n s - M a i n e f f e c t s a n d o t h e r e f f e c t s
S t a n d a r d i z e d E f f e c t s ( t - v a l u e s )
- 3 , 0
- 2 , 5
- 2 , 0
- 1 , 5
- 1 , 0
- 0 , 5
0 , 0
0 , 5
1 , 0
1 , 5
2 , 0
2 , 5
3 , 0
ExpectedNormalValue
, 0 1
, 0 5
, 1 5
, 3 5
, 5 5
, 7 5
, 9 5
, 9 9

14. Interpretação dosInterpretação dos
resultadosresultados
 Os efeitos principais são significativos.Os efeitos principais são significativos.
 O efeito de interação entre temperatura eO efeito de interação entre temperatura e
concentração é significativo.concentração é significativo.
 Não há interação entre a concentração eNão há interação entre a concentração e
os outros fatores.os outros fatores.
 Não há interação entre os três fatores.Não há interação entre os três fatores.

15. Modelo estatísticoModelo estatístico
 Y (x1,x2,x3) = Bo + B1x1 + B2x2 + B3x3Y (x1,x2,x3) = Bo + B1x1 + B2x2 + B3x3
= B12 x1x2.= B12 x1x2.
 Y = 67,3 + 11,4*T – 6,9*Cat + 4,4*Conc –Y = 67,3 + 11,4*T – 6,9*Cat + 4,4*Conc –
4,3 * T * Con.4,3 * T * Con.

16. Planejamento fatorialPlanejamento fatorial
2244
 Ao planejamento anterior adicionamos maisAo planejamento anterior adicionamos mais
uma variável (fator)uma variável (fator)
 Resultados sem repetições.Resultados sem repetições.
 Pode-se calcular:Pode-se calcular:
 média globalmédia global
 Quatro fatores principaisQuatro fatores principais
 Seis interações de dois fatoresSeis interações de dois fatores
 Quatro interações de três fatoresQuatro interações de três fatores
 Uma interação de quatro fatoresUma interação de quatro fatores

17. Planejamento fatorialPlanejamento fatorial
2244
 Exemplo (p105): Rendimento como função de:Exemplo (p105): Rendimento como função de:
 11 - Temperatura- Temperaturaoo
C (-) 40 e (+) 60C (-) 40 e (+) 60
 22 - Catalisador Tipo (-) A e (+) B- Catalisador Tipo (-) A e (+) B
 33 - Concentração Mol (-) 1,0 e (+) 1,5- Concentração Mol (-) 1,0 e (+) 1,5
 44 – pH (-) 7,0 e (+) 6,0– pH (-) 7,0 e (+) 6,0

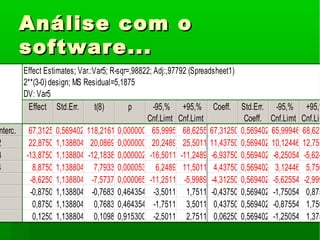
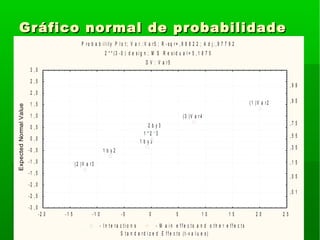
18. 1 T[40;60]; 2 K[A;B]; 3 C[1;1,5];1 T[40;60]; 2 K[A;B]; 3 C[1;1,5];
pH[7;6]pH[7;6]
 Ensaio 1 2 3 4 resp Ensaio 1 2 3 4 respEnsaio 1 2 3 4 resp Ensaio 1 2 3 4 resp
 1 - - - - 54 9 - - - + 521 - - - - 54 9 - - - + 52
 2 + - - - 85 10 + - - + 872 + - - - 85 10 + - - + 87
 3 - + - - 49 11 - + - + 493 - + - - 49 11 - + - + 49
 4 + + - - 62 12 + + - + 644 + + - - 62 12 + + - + 64
 5 - - + - 64 13 - - + + 645 - - + - 64 13 - - + + 64
 6 + - + - 94 14 + - + + 946 + - + - 94 14 + - + + 94
 7 - + + - 56 15 - + + + 587 - + + - 56 15 - + + + 58
 8 + + + - 70 16 + + + + 738 + + + - 70 16 + + + + 73

19. ProcedimentosProcedimentos
 Os ensaios não foram repetidos !Os ensaios não foram repetidos !
 Cálculo da média e dos efeitos : procede-Cálculo da média e dos efeitos : procede-
se da forma apresentada exemplos jáse da forma apresentada exemplos já
analisados....analisados....
 Obtemos os efeitos, exceto para a média,Obtemos os efeitos, exceto para a média,
e dividindo o valor por 2 temos ase dividindo o valor por 2 temos as
estimativas dos coeficientes.estimativas dos coeficientes.
 Estimativa do erro: como os ensaios nãoEstimativa do erro: como os ensaios não
foram repetidos temos outra possibilidadeforam repetidos temos outra possibilidade

20. Estimativa do erroEstimativa do erro
 A medida que o número de fatoresA medida que o número de fatores
aumenta, o número de termos do modeloaumenta, o número de termos do modelo
matemático também aumenta.matemático também aumenta.
 No modelo temos agora 16 termos...No modelo temos agora 16 termos...
 ““podemos esperar que os coeficientes dopodemos esperar que os coeficientes do
modelo obedeçam uma certamodelo obedeçam uma certa
hierarquia ..., esperamos que os efeitoshierarquia ..., esperamos que os efeitos
principais sejam mais importantes...”principais sejam mais importantes...”

21. Efeitos calculadosEfeitos calculados
 Média : 67,188Média : 67,188
 Efeitos principaisEfeitos principais
 Temperatura (1) 22,875 ; Catalisador (2) -14,125Temperatura (1) 22,875 ; Catalisador (2) -14,125
 Concentração (3) 8,875 ; pH (4) 0,875Concentração (3) 8,875 ; pH (4) 0,875
 Interações:Interações:
 (12) =-8,625; (13)=-0,625; (14)=0,875; (23)=-(12) =-8,625; (13)=-0,625; (14)=0,875; (23)=-
0,625; (24)=0,875; (34)=0,3750,625; (24)=0,875; (34)=0,375
 (123)=0,875; (124)=-0,125; (134)=-0,625;(123)=0,875; (124)=-0,125; (134)=-0,625;
(234)=0,375; (1234)=0,375(234)=0,375; (1234)=0,375

22. Effect Estimates; Var.:Var5; R-sqr=,99984; Adj:,9976 (Spreadsheet11)
2**(4-0) design; MS Residual=,5625
DV: Var5
tor
Effect Std.Err. t(1) p -95,%
Cnf.Limt
+95,%
Cnf.Limt
Coeff. Std.Err.
Coeff.
-95,%
Cnf.Limt
an/Interc.
Var1
Var2
Var3
Var4
y 2
y 3
y 4
y 3
y 4
y 4
*3
*4
*4
*4
67,1875 0,187500 358,3333 0,001777 64,8051 69,56991 67,18750 0,187500 64,8050
22,8750 0,375000 61,0000 0,010435 18,1102 27,63983 11,43750 0,187500 9,0550
-14,1250 0,375000 -37,6667 0,016897 -18,8898 -9,36017 -7,06250 0,187500 -9,4449
8,8750 0,375000 23,6667 0,026883 4,1102 13,63983 4,43750 0,187500 2,0550
0,8750 0,375000 2,3333 0,257762 -3,8898 5,63983 0,43750 0,187500 -1,9449
-8,6250 0,375000 -23,0000 0,027662 -13,3898 -3,86017 -4,31250 0,187500 -6,6949
-0,6250 0,375000 -1,6667 0,344042 -5,3898 4,13983 -0,31250 0,187500 -2,6949
0,8750 0,375000 2,3333 0,257762 -3,8898 5,63983 0,43750 0,187500 -1,9449
-0,6250 0,375000 -1,6667 0,344042 -5,3898 4,13983 -0,31250 0,187500 -2,6949
0,8750 0,375000 2,3333 0,257762 -3,8898 5,63983 0,43750 0,187500 -1,9449
0,3750 0,375000 1,0000 0,500000 -4,3898 5,13983 0,18750 0,187500 -2,1949
0,8750 0,375000 2,3333 0,257762 -3,8898 5,63983 0,43750 0,187500 -1,9449
-0,1250 0,375000 -0,3333 0,795167 -4,8898 4,63983 -0,06250 0,187500 -2,4449
-0,6250 0,375000 -1,6667 0,344042 -5,3898 4,13983 -0,31250 0,187500 -2,6949
0,3750 0,375000 1,0000 0,500000 -4,3898 5,13983 0,18750 0,187500 -2,1949

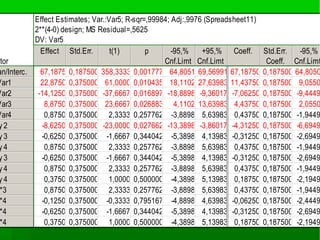
23. Estimativa do erroEstimativa do erro
 A análise dos resultados mostra que os efeitosA análise dos resultados mostra que os efeitos
principais e as interações de dois fatores sãoprincipais e as interações de dois fatores são
suficientes para descrever o modelosuficientes para descrever o modelo
 As interações de três ou mais efeitos podem serAs interações de três ou mais efeitos podem ser
atribuídas a flutuações inerentes ao processo.atribuídas a flutuações inerentes ao processo.
“ruído”“ruído”
 Usando os para a estimativa da variância de umUsando os para a estimativa da variância de um
efeito; assim para os cinco valores temos:efeito; assim para os cinco valores temos:
 Variância = [(0,875)2+ ....+(0,375)Variância = [(0,875)2+ ....+(0,375)22
]/5= 0,291]/5= 0,291
 Erro padrão para o efeito será 0,54.Erro padrão para o efeito será 0,54.

25. Gráfico de Pareto...Gráfico de Pareto...

26. Análise por gráficos...Análise por gráficos...
 ““A análise por gráficos normais é uma técnicaA análise por gráficos normais é uma técnica
alternativa, para tentarmos distinguir, nosalternativa, para tentarmos distinguir, nos
resultados de um planejamento, os valores queresultados de um planejamento, os valores que
correspondem realmente aos efeitos, doscorrespondem realmente aos efeitos, dos
valores que são devidos ao ruído”valores que são devidos ao ruído”
 Utiliza-se do conceito de probabilidadeUtiliza-se do conceito de probabilidade
cumulativa.... partindo-se do gráfico decumulativa.... partindo-se do gráfico de
probabilidade de uma distribuição normalprobabilidade de uma distribuição normal
padronizada...padronizada...

27. GráficosGráficos
 Um gráfico da probabilidade cumulativa numaUm gráfico da probabilidade cumulativa numa
distribuição normal é uma curvadistribuição normal é uma curva
monotonicamente crescente (curva B...p.118)monotonicamente crescente (curva B...p.118)
 A curva pode ser transformada em uma reta porA curva pode ser transformada em uma reta por
meio de uma modificação na escala do eixo dasmeio de uma modificação na escala do eixo das
ordenadas....ordenadas....
 Mudando-se o eixo para uma escala deMudando-se o eixo para uma escala de
probabilidade normal os pontos ajustam-seprobabilidade normal os pontos ajustam-se
aproximadamente a uma reta....aproximadamente a uma reta....
 ““expandir a escala simetricamente em torno doexpandir a escala simetricamente em torno do
ponto representado por 0,5 de modo a “esticar”ponto representado por 0,5 de modo a “esticar”
as duas pontas do S”as duas pontas do S”

28. Exemplo:planejamentoExemplo:planejamento
2244
 No gráfico de probabilidade cumulativa osNo gráfico de probabilidade cumulativa os
pontos centrais se ajustam a uma reta quepontos centrais se ajustam a uma reta que
cruza a probabilidade acumulada de 50%cruza a probabilidade acumulada de 50%
aproximadamente sobre o ponto zero dasaproximadamente sobre o ponto zero das
abscissas.abscissas.
 Pode-se observar no gráfico da probabilidadePode-se observar no gráfico da probabilidade
cumulativa que os efeitos principais: (1)cumulativa que os efeitos principais: (1)
temperatura; (2) Catalisador; (3) concentração etemperatura; (2) Catalisador; (3) concentração e
a interação (12) são realmente significativosa interação (12) são realmente significativos
 Os efeitos são mais significativos, quanto maisOs efeitos são mais significativos, quanto mais
afastados para direita ou esquerda.afastados para direita ou esquerda.

29. Gráfico p.122Gráfico p.122

30. 3.53.5 EVOP –EVOP – OpOperaçãoeração
EvEvolucionariaolucionaria
 Melhora das condições de processo em largaMelhora das condições de processo em larga
escala.escala.
 Na prática o processo continua sendo operadoNa prática o processo continua sendo operado
dentro de parâmetros estabelecidos na suadentro de parâmetros estabelecidos na sua
partida.partida.
 Como se busca um ajuste fino, pequenasComo se busca um ajuste fino, pequenas
alterações dos parâmetros são implementadas.alterações dos parâmetros são implementadas.
 A forma recomendada é um planejamento emA forma recomendada é um planejamento em
dois níveis.dois níveis.
 Avaliação do processo (p.125)Avaliação do processo (p.125)

31. EVOP...EVOP...
 Planejamento fatorial com ponto central...Planejamento fatorial com ponto central...
 Ponto centralPonto central AA (condições iniciais...)(condições iniciais...)
 Experimentos em condições próximas.... B, C ,Experimentos em condições próximas.... B, C ,
D e E...D e E...
 Identificação da condição mais favorável...Identificação da condição mais favorável...
uma espécie de “seleção natural”uma espécie de “seleção natural”
 Proposição de possíveis deslocamentos...Proposição de possíveis deslocamentos...

32. BLOCAGEMBLOCAGEM
 Possibilidade de neutralizar (minimizar) efeitosPossibilidade de neutralizar (minimizar) efeitos
indesejáveisindesejáveis
 Exemplo: diferentes lotes de matéria primaExemplo: diferentes lotes de matéria prima
 Em um planejamento 23, o efeito menosEm um planejamento 23, o efeito menos
importante é a interação 123...importante é a interação 123...
 Se temos dois lotes podemos executar oSe temos dois lotes podemos executar o
planejamento de forma a confundí-lo com esteplanejamento de forma a confundí-lo com este
efeito...efeito...

33. Planejamento 2Planejamento 233
em dois blocos...em dois blocos...
Ensaio 1 2 3 123 bloco lote
1 - - - - I A
2 + - - + II B
3 - + - + II B
4 + + - - I A
5 - - + + II B
6 + - + - I A
7 - + + - I A
8 + + + + II B

34.  AplicaçõesAplicações
 Livro BrunsLivro Bruns
 3 A.1 hidrólise de enzimas3 A.1 hidrólise de enzimas
 3 A.2 voltametria cíclica do azul de metileno3 A.2 voltametria cíclica do azul de metileno
 3 A.3 Tempo de retenção em CLAE3 A.3 Tempo de retenção em CLAE
 3 A. 4 Separação de gases....3 A. 4 Separação de gases....
 3 A.8 Desenvolvimento de um detergente.3 A.8 Desenvolvimento de um detergente.