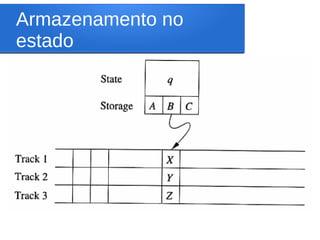
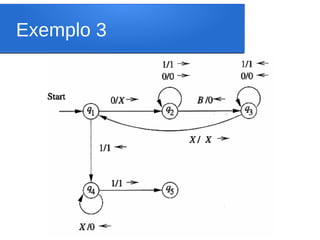
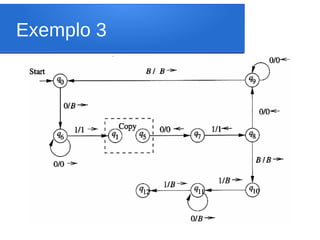
O documento discute técnicas de programação para máquinas de Turing, incluindo armazenamento no estado, várias trilhas e subrotinas. Estas técnicas permitem representar MTs de forma mais modular e eficiente, sem aumentar seu poder de cálculo. Exemplos ilustram como estas técnicas podem ser usadas para projetar MTs para problemas como aceitação de linguagens regulares e multiplicação.

1. Máquinas de Turing com
modificações
Yuri Tavares dos Passos

2. Técnicas de programação
para MTs
● Dar uma ideia do poder de cálculo das
MTs
● Mostrar que tem o mesmo poder de um
computador
● Facilitar o projeto de MTs

3. Técnicas de programação
para Mts
● São elas:
– Armazenamento no estado
– Várias trilhas
– Subrotinas

4. Armazenamento no
estado

5. Armazenamento no
estado
● Q armazena algum(ns) dado(s) para
utilização
– Possui um componente que indica o estado
– Possui um outro componente que armazena
uma quantidade finita de símbolos

6. Armazenamento no
estado
● Q passa a ser um conjunto de tuplas
● Q = Q' x Г
– Q = {q0,q1} x {0,1,B}
– Q = {(q0,0),(q1,0),(q0,1),(q1,1),(q0,B),(q1,B)}

7. Exemplo 1
● MT que aceita 01*+10*
● M = (Q,{0,1},{0,1,B},δ,(q0,B),B,{(q1,B)})
● Q = {q0,q1} x {0,1,B}
● A primeira parte significa:
– q0 indica que ainda vai ler o primeiro símbolo.
– q1 indica que já leu o primeiro símbolo.
● A segunda parte indica qual foi o primeiro caractere
lido. B indica que nenhum foi lido.

8. Exemplo 1
● Para a = 0 ou a = 1:
– δ((q0,B),a) = ((q1,a),a,R)
– δ((q1,a),a) = ((q1,a),a,R)
– δ((q1,a),B) = ((q1,B),B,R)
– δ((q1,a),a) é indefinido, logo a MT pára.

9. Armazenamento no
estado
● Exercício:
– Fazer o diagrama de transições do Exemplo 1

10. Várias trilhas
● Consiste em adicionar mais trilhas
● A MT continua com uma cabeça de leitura
apenas.
● Г e Σ são conjuntos de tuplas
● Σ = Σ1 x Σ2 x … x Σn
● Г = Г1 x Г2 x … x Гn

11. Exemplo 2
● Uma MT que aceite
– L = {wcw | w está em {0,1}*}
● M = (Q,Σ,Г,δ,(q1,B),(B,B),{(q9,B)})
● Q = {q1,…,q9} x {0,1,B}
● Σ = {(B,0),(B,1),(B,c)}
● Г = {B,*} x {0,1,c,B}
– * indica que o caractere foi “marcado”
– Ausência de marcador, indica que ela ainda deverá ser lido

12. Exemplo 2
● ∀a,b tal que a ∈ {0,1} ou b ∈ {0,1}, δ será:
– δ((q1,B),(B,a)) = ((q2,a),(*,a),R)
– δ((q2,a),(B,b)) = ((q2,a),(B,b),R)
– δ((q2,a),(B,c)) = ((q3,a),(B,c),R)
– δ((q3,a),(*,b)) = ((q3,a),(*,b),R)

13. Exemplo 2
● Cont.:
– δ((q3,a),(B,a)) = ((q4,B),(*,a),L)
– δ((q4,B),(*,a)) = ((q4,B),(*,a),L)
– δ((q4,B),(B,c)) = ((q5,B),(B,c),L)
– δ((q5,B),(B,a)) = ((q6,B),(B,a),L)
– δ((q6,B),(B,a)) = ((q6,B),(B,a),L)

14. Exemplo 2
● Cont.:
– δ((q6,B),(*,a)) = ((q1,B),(*,a),R)
– δ((q5,B),(*,a)) = ((q7,B),(*,a),R)
– δ((q7,B),(B,c)) = ((q8,B),(B,c),R)
– δ((q8,B),(*,a)) = ((q8,B),(*,a),R)
– δ((q8,B),(B,B)) = ((q9,B),(B,B),R)

15. Considerações
● O uso de armazenamento de controle e
várias trilhas não aumentam o poder da
MT
● Por quê?

16. Considerações
● O uso de armazenamento de controle e
várias trilhas não aumentam o poder da MT
● Por quê?
– Porque o uso de tuplas não muda a definição
da MT.
● Um conjunto de tuplas continua sendo um conjunto!
● Há apenas uma mudança de representação.

17. Subrotinas
● Consistem em projetar uma pequena parte
da MT para ser usada em outra, maior
● Modulariza a MT
● Lembra os procedimentos de programação

18. Exemplo 3
● Uma MT que realiza multiplicação
● Entrada: 0m10n1
● Saída: 0mn

19. Exemplo 3
● Estratégia:
– Em geral, haverá uma string 0i10n10kn
– Em uma etapa básica, teremos 0i-110n10(k+1)n
– Copiamos o grupo de n 0s até o fim, m vezes
– A etapa final é trocar os 1s iniciais por B

20. Exemplo 3
● A segunda etapa, pode ser feita por uma
subrotina Copy
● Ela terá a seguinte descrição instantânea
ao final da execução:
– 0m-k1q10n10(k-1)n *⊢ 0m-k1q50n10kn

21. Exemplo 3

22. Exemplo 3

23. Exercícios
● Projete as MTs da aula anterior usando estas
técnicas
● Projete uma subrotina para mover a cabeça de um
MT de sua posição atual para a direita, saltando
sobre todos os 0s, até chegar a um 1 ou B. Se a
posição atual não contiver 0, a MT deve parar.
Você poderá supor que não existem símbolos de
fita além de 0, 1 e B. Assim, use essa subrotina
para projetar uma MT que aceite todos os strings
de 0s e 1s que não em dois 1s em uma linha.

24. Referência
● [1] HOPCROFT, John E.; ULLMAN, Jeffrey
D.; MOTWANI, Rajeev. Introdução à teoria
de autômatos, linguagens e computação.
[Rio de Janeiro]: Campus, c2003. p. 328-
352
● Imagens da versão em inglês