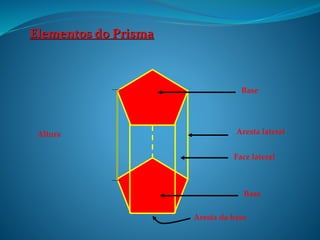
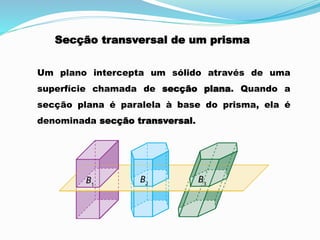
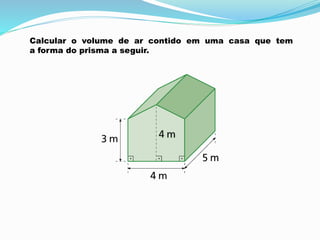
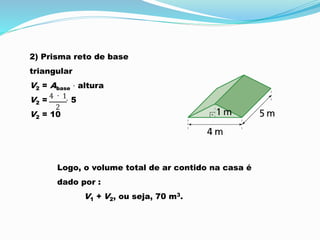
O documento explica como calcular o volume de um prisma usando o Princípio de Cavalieri. O princípio estabelece que sólidos com a mesma altura têm volumes iguais se suas seções transversais tiverem a mesma área. O volume de um prisma é igual à área da base multiplicada pela altura. O documento fornece um exemplo de cálculo do volume de ar contido em uma casa com a forma de dois prismas.

1. Calculando o volume através do
Princípio de Cavalieri
Isaura Aparecida Torse de Almeida

2. O que você consegue observar de comum
entre os sólidos abaixo?

3. Prisma é um sólido geométrico que
possui duas faces poligonais opostas,
paralelas e congruentes, chamadas
bases, separadas por uma distância
chamada altura.
As demais faces possuem forma de
paralelogramos, sendo os lados os
segmentos que unem os vértices
correspondentes da suas bases.

4. Elementos do Prisma
Base
Base
Aresta da base
Aresta lateral
Face lateral
Altura

5. O prisma é regular quando
suas bases forem polígonos regulares.
Quanto à base, os prismas mais comuns são:

6. Como podemos calcular o volume de um prisma qualquer?
Observe as pilhas de bolacha:
O que eles tem em comum?

7. Observando as pilhas, é possível notar que:
 a altura das duas pilhas é a mesma, pois têm a
mesma quantidade de bolachas;
As bolachas das duas pilhas ficam à mesma
altura da mesa e têm
a mesma área, pois são idênticas;
 a segunda pilha tem o mesmo volume da
primeira, já que é formada pelas mesmas
bolachas, portanto, ocupa a mesma porção
do espaço.

8. O princípio de Cavalieiri
Bonaventura Cavalieri foi um matemático
italiano, discípulo de Galileu, que criou um
método capaz de determinar áreas e
volumes de sólidos com muita facilidade,
denominado princípio de Cavalieri.
Este princípio consiste em estabelecer
que dois sólidos com a mesma altura têm
volumes iguais se as secções planas de
iguais altura possuírem a mesma área.

9. Secção transversal de um prisma
Um plano intercepta um sólido através de uma
superfície chamada de secção plana. Quando a
secção plana é paralela à base do prisma, ela é
denominada secção transversal.

10. Podemos verificar que, para
todos os prismas, uma vez que,
os prismas podem ter bases
diferentes, o volume pode ser
obtido calculando-se a área da
base e multiplicando-se pela
medida da altura:
V= A x h, (A é a medida da
superfície da base do prisma,
dada pelo valor do comprimento
x o comprimento da largura).

11. Calcular o volume de ar contido em uma casa que tem
a forma do prisma a seguir.

12. 1) Prisma reto-retângulo
V1 = Abase ⋅ altura
V1 = 4 ⋅ 5 ⋅ 3
V1 = 60
Vamos decompor a figura da casa em dois
prismas.

13. 2) Prisma reto de base
triangular
V2 = Abase ⋅ altura
V2 = ⋅ 5
V2 = 10
Logo, o volume total de ar contido na casa é
dado por :
V1 + V2, ou seja, 70 m3.

14. Referências:
http://diadematematica.com/vestibular/conteudo/GE_PRI2.htm (acesso
em 20/09/2014)
http://pessoal.sercomtel.com.br/matematica/geometria/prisma/prisma.
htm (acesso em 20/09/2014)
http://www.educ.fc.ul.pt/icm/icm2002/icm204/solidos_geometricos.htm
(acesso em 21/09/2014)
www.escolaomega.com.br/.../2013.05.15_poliedros_matematica2.ppt
(acesso em 21/09/2014)
http://www.uff.br/cdme/pdp/pdp-html/pdp-br.html (acesso em
21/09/2014)