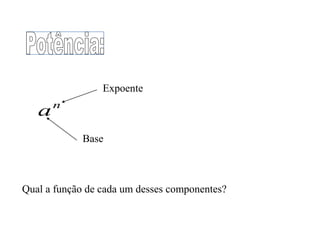
Neste documento, são explicadas as propriedades e operações com potências. São descritas regras para elevar números à potência, multiplicar, dividir e elevar potências à potência. Exemplos ilustram como aplicar estas regras para simplificar expressões com potências.

2. Expoente
n
a
Base
Qual a função de cada um desses componentes?

3. Exemplo:
12 5 5 5 5 5 5 5 5 5 5
 5 5
5 12 vezes
244 .140 .625

4. 1ª) Toda potência de expoente 1 é igual a base.
31 3 41 4
2ª) Toda potência de expoente zero e base não
nula é igual a 1.
7 0
1 ( 5) 0 1

5. 3ª) Todo número “a”, diferente de zero, temos
que vale a seguinte propriedade:
n 1 Onde “n” é um expoente que pode
a
a n ser um número inteiro.
2 1 1
5
52 25
3 1 1 1 1
( 4)
( 4)3 4 4 4 64 64

6. 5 2
4ª) O produto 8 8 pode ser escrito na forma
de uma única potência?
85 8 2 8 8  8 8 8
8  8  87
5 vezes 2 vezes
Para multiplicarmos potências que
possuem a mesma base, conservamos a
base e somamos os expoentes, assim:
85 82 85 2
87

7. 3 5
5ª) Será que a divisão 4 : 4 pode ser escrito na
forma de uma única potência?
3 vezes
 

3 5 43 4 4 4 4 4 4 1 1 2
4 :4 4
45 4 4  4
4  4 4 4 4 4 4 4 4 42
5 vezes
Para dividirmos potências que possuem a
mesma base, conservamos a base e
subtraímos os expoentes, assim:
43 : 45 43 5
4 2

8. 6ª) Agora, queremos escrever 11 6 4 como o
produto de duas potências
11 6
4
11 6 11 6 11 6 11 6 11 11 11 11 6 6 6 6 114 64

 
o fator 11 4 aparece 4 vezes
Para elevar o produto de números inteiros
a uma potência, elevamos cada fator a
essa potência, assim:
4 4 4
11 6 11 6

9. 7ª) Como calcular a potência de uma potência?
Por exemplo: 52 3
2 3
5 52 52 52 555555 56
Para elevar uma potência a um expoente,
mantemos a base e multiplicamos os
expoentes, assim:
2 3
5 52 3 56

10. 8ª) E como fazer potência de frações? Por
2
2
exemplo:
3
2
2 2 2 22 4
3 3 3 32 9
Para fazer potência de frações, basta
calcular a potência do numerador e a
potência do denominador, assim:
2
2 22 4
3 32 9

11. 1)Efetue cada uma das expressões aplicando as propriedade:
2 1
a ) 4 23 b) 2 5 3 2
23 : 25
c) d )9 2 38 : 35
3 2
2 8
20
22 5 2 3
e) f ) 2,3
518
2)Sabendo que a = 2 e b = 3, faça o que se pede e responda as perguntas:
a)Calcule a b 2
b) Calcule a 2 b2
2
c) Será que a b a2 b2 ?