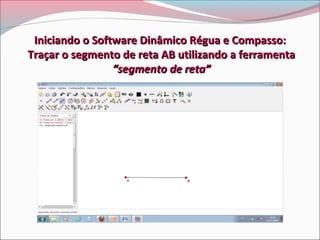
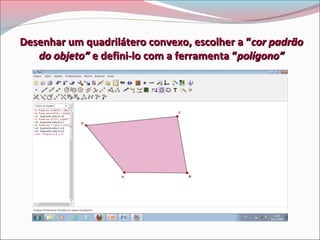
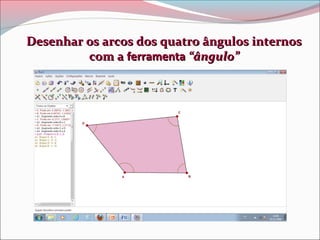
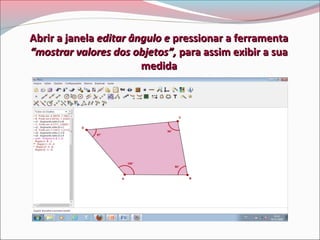
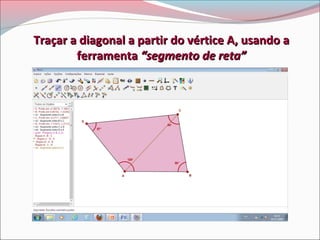
Este documento descreve um projeto de ensino sobre o Teorema da Soma dos Ângulos Internos de um Polígono Convexo Plano. O projeto envolve aulas práticas com alunos utilizando o software Régua e Compasso para construir polígonos e responder perguntas, com o objetivo de entender e verificar o teorema.

1. Curso de Informática Educativa I
Projeto de Execução
Aluna: Sílvia Regina Guedes da Silva
Tutora: Marina Ribeiro Barros Dias
Polo: Campo Grande - Grupo: 6

2. TEMA CENTRAL
Teorema da Soma dos Ângulos Internos de um Polígono
Convexo Plano
TEMAS DE APOIO
 Soma dos ângulos internos de um quadrilátero;
 Soma dos ângulos internos de um hexágono;
 Soma dos ângulos internos de um eneágono;
 Verificação do Teorema da Soma dos Ângulos
Internos de um Polígono Convexo Plano.

3. OBJETIVOS PRINCIPAIS DESSE PROJETO
 Reverter o índice de aproveitamento dos alunos, visando
o aumento das competências e habilidades necessárias à
aprendizagem, principalmente na Geometria;
 Estimular o raciocínio lógico dos alunos;
 Reconhecer um polígono convexo plano;
 Entender o conceito de diagonal de um polígono;
 Identificar e calcular a soma dos ângulos internos de um
polígono convexo plano;
 Verificação do Teorema da Soma dos Ângulos Internos de
um Polígono Convexo Plano.

4. Primeira Aula (2 tempos): Pesquisa e Produção
Textual
Os alunos serão divididos em grupos de três por
computador e farão uma resumida pesquisa sobre os
conceitos básicos de linha poligonal, polígonos e
polígonos convexos ou côncavos, no laboratório de
informática.
O professor solicitará que seja elaborada uma
produção textual, em folha de papel A4, sobre o que
foi entendido do conteúdo lido pelo grupo.

5. Segunda Aula (2 tempos) : Construção do Quadrilátero
Convexo Plano Utilizando o Software Dinâmico Régua e
Compasso
Os alunos construirão o quadrilátero convexo plano
utilizando o software dinâmico Régua e Compasso
mediante a orientação do professor. A construção será
gravada no pen drive, para uma posterior apresentação
no datashow.
Algumas funções do Régua e Compasso serão
apresentadas aos alunos, para que eles comecem a se
familiarizar com o software.

6. Iniciando o Software Dinâmico Régua e Compasso:
Traçar o segmento de reta AB utilizando a ferramenta
“segmento de reta”

7. Desenhar um quadrilátero convexo, escolher a “cor padrão
do objeto” e defini-lo com a ferramenta “polígono”

8. Desenhar os arcos dos quatro ângulos internos
com a ferramenta “ângulo”

9. Abrir a janela editar ângulo e pressionar a ferramenta
“mostrar valores dos objetos”, para assim exibir a sua
medida

10. Professor, antes de finalizar o quadrilátero é
necessário que seja explicado aos seus alunos o
conceito de diagonal de um polígono, tendo em
vista as perguntas do questionário relacionado
ao assunto.
Segmento de reta que une dois pontos não
consecutivos.

11. Traçar a diagonal a partir do vértice A, usando a
ferramenta “segmento de reta”

12. Terceira Aula (2 tempos): Aplicação do Questionário
Sobre as Conclusões na Construção do Polígono
O professor irá propor aos seus alunos alguns
questionamentos com o objetivo de estabelecer
conclusões acerca da soma dos ângulos internos de
um polígono convexo plano.
Essa etapa será realizada individualmente.

13. Questionário
a) O que aconteceu com o quadrilátero após utilizar a
ferramenta (mover ponto)?
____________________________________________
__________________________________________
b) Após traçar a diagonal AC a que conclusão você
chegou?
____________________________________________
__________________________________________

14. c) Se chamarmos n de números de lados, então o
número de triângulos é quantas vezes menos esse
n? ____________________
d) Qual é o resultado da soma dos ângulos internos
desse polígono construído?
S4 = _________
O objetivo de tais questionamentos é avaliar a
percepção e a conclusão dos alunos acerca do
assunto abordado.

15. SUGESTÃO DE ATIVIDADE PARA EXERCITAR
Vamos exercitar mais?
Construa os polígonos abaixo utilizando o software Régua e
Compasso, depois responda aos questionamentos da terceira
aula referentes à essas novas construções geométricas:
a) Um hexágono convexo qualquer.
b) Um eneágono convexo qualquer.
Todas as construções serão gravadas no pen drive, para uma
futura apresentação no datashow, pelos alunos.

16. De volta à sala de aula, o professor contextualizará o processo
de descoberta dos alunos, apresentando o Teorema da Soma
dos Ângulos Internos do Polígono Convexo e irá propor
exercícios de aprofundamento para aplicação do que foi
aprendido. A soma dos ângulos internos de um polígono de n
lados é igual a 180° vezes o número de lados menos 2, pois é o
número de triângulos que formam o polígono. Podemos
concluir então que:
Si = 180° · (n – 2)
O professor utilizará listas de exercícios, visando o
aprofundamento do conteúdo.

17. Quarta Aula (2 tempos): Exposição do Trabalho
dos Alunos
Cada grupo de alunos fará uma exposição do seu
trabalho para a turma através de uma apresentação
de slides (arquivo em PowerPoint - slideshare)
utilizando o datashow com as construções
geométricas e suas conclusões.

18. AVALIAÇÃO
A avaliação será realizada durante todas as aulas
mediante a apresentação da produção textual, da
participação nas atividades propostas pelo
professor (laboratório de informática e sala de
aula), pelo cooperativismo e pelo respeito entre os
grupos.

19. CONCLUSÕES
Esse projeto tem o objetivo de mostrar que a Matemática
se torna muitas vezes mais lúdica, pois a Geometria se
transforma em um jogo, realizando os passos para a
construção das figuras geométricas, seguindo as regras e
assim obtendo o resultado esperado;
Acredita-se que a utilização de materiais concretos e
tecnológicos na pedagogia moderna auxilia e contribua
para a eficiência do aprendizado do aluno. O software
dinâmico Régua e Compasso tem uma função significativa
na interpretação do que é proposto e o aluno percebe que
a Matemática está dentro de seu cotidiano através das
atividades que são realizadas.

20. REFERÊNCIAS BIBLIOGRÁFICAS
GRAVINA, M. A. Os ambientes de geometria dinâmica e o
pensamento hipotético-dedutivo. Tese de Doutorado, Universidade
Federal do Rio Grande do Sul (UFRGS). Porto Alegre. 2001.
<http://www.brasilescola.com/matematica/tipos-poligonos.htm>
<http://geometria-semlimite.com.br/teoquinta.html>
OLIVEIRA, M. K. Vigotsky, aprendizado e desenvolvimento: Um
processo sócio-histórico. São Paulo: Scipione, 4ª ed. - 1997.
SOFTWARE RÉGUA E COMPASSO. Disponível em:
<http://www.professores.uff.br/hjbortol/car/> Acesso em 26 de
setembro de 2013.