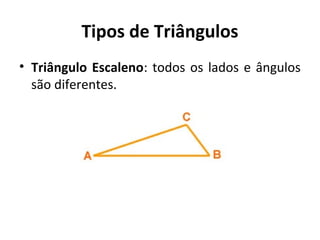
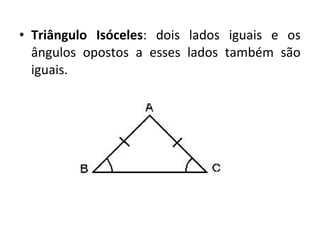
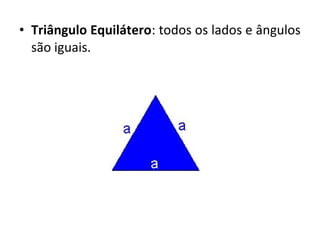
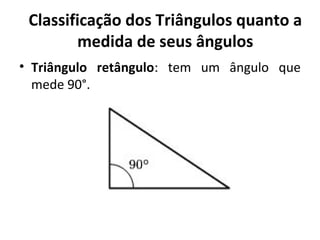
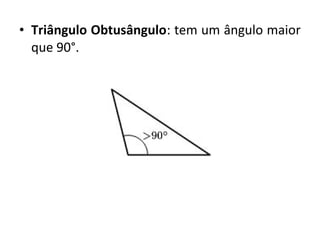
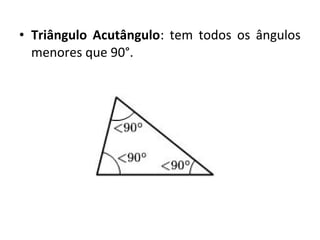
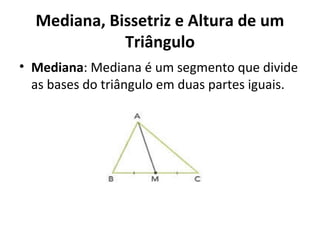
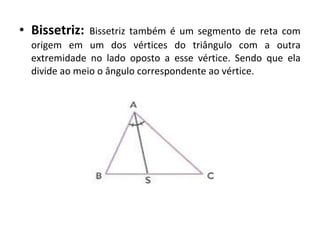
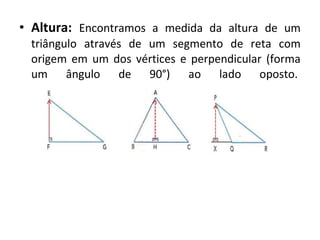
Este documento discute a história e conceitos básicos de geometria, incluindo os tipos de triângulos e suas classificações. Ele também apresenta o software Cabri-Géomètre, que permite construções geométricas interativas para explorar e entender melhor esses conceitos. Uma atividade prática é fornecida para aplicar esses conceitos usando o software.

1. Conceitos Básicos de Geometria
utilizando o Cabri-Géomètre
ORLANDO GITTI JUNIOR
UFF – NTEM 2014
PÓLO VOTUPORANGA/SP

2. A Geometria: Suas origens na História
A palavra geometria é derivada do grego “geometrein”,
sendo “geo”= terra e “metrein”= medir. A origem provável da
Geometria vem da medição dos terrenos do Antigo Egito. Porém
temos registros na História de que outras civilizações antigas,
como Babilônia, China e Índia também possuíam conhecimentos
geométricos. A Geometria surgiu da necessidade de melhorar os
sistema de arrecadação de impostos de áreas rurais, sendo os
primeiros passos dados pelos egípcios para desenvolvê-la.

3. No chamado “Livros dos Mortos” do Egito
antigo constava que roubar a terra do vizinho
era considerado uma ofensa tão grave como
quebrar um juramento ou assassinar alguém.
Naquela época, não existiam marcos fronteiriços
e os agricultores, os administradores de
templos, palácios e demais unidades produtivas
fundadas na agricultura não tinham referência
clara do limite das suas posses, tanto para
cultivo, como para pagamento de impostos
devidos aos governantes, de acordo com a
medida da sua extensão.

4. A Geometria, em seus primórdios, era uma
ciência empírica, ou seja, experimental. As medições
baseavam-se em algumas regras para se chegar a
resultados aproximados. As civilizações ora
acertavam em seus cálculos, ora erravam, pois não
havia um rigor matemático que os ajudasse em seus
cálculos. Mas, somente a partir do conhecimento
desenvolvido pelos matemáticos gregos é que a
Geometria pôde ser estabelecida como teoria
dedutiva. Assim, através do raciocínio dedutivo,
começaram a provar a veracidade das proposições
através de Hipóteses e Demonstrações.

5. Tales de Mileto (624--547 a.C.) e seu discípulo Pitágoras (572-497
a.C.) coligiram todo o conhecimento do Egito, da Etúrria, da Babilônia, e
mesmo da Índia, para desenvolvê-los e aplicá-los à matemática, navegação e
religião. A curiosidade crescia e os livros sobre Geometria eram muito
procurados. Um compasso logo substituiu a corda e a estaca para traçar
círculos, e o novo instrumento foi incorporado ao arsenal dos geômetras. O
conhecimento do Universo aumentava com rapidez e a escola pitagórica
chegou a afirmar que a Terra era esférica, e não plana. Surgiam novas
construções geométricas, e suas áreas e perímetros eram agora fáceis de
calcular.

6. Pitágoras, após suas viagens ao Egito e à Babilônia, estabeleceu-se
em Crotona (cidade ao sul da Itália) e fundou o que chamamos de “Escola
Pitagórica”: um culto religioso e filosófico que pregava a purificação do
espírito através da música e da matemática. Porém, não existem documentos
matemáticos produzidos por eles, que tenham sido encontrados. O que
temos registrado na História da Matemática, um resumo feito por Proclo,
comentando os "Elementos" de Euclides, do século V a.C., referindo-se a
Tales de Mileto como o introdutor da Geometria na Grécia, por importação
do Egito.

7. As influências da Geometria nas Ciências físicas foi muito
importante. Como exemplo, o astrônomo Johannes Kepler
mostrou que as relações entre as velocidades máximas e
mínimas dos planetas, propriedades intrínsecas das órbitas,
estavam em razões harmônicas (relações musicais), afirmando
ser uma música que só podia ser percebida com os ouvidos da
alma (a mente do geômetra). A introdução do “Plano
Cartesiano” também trouxe uma solução simplificada para os
problemas de Álgebra, transformando-os em problemas de
Geometria.

8. Tipos de Triângulos
• Triângulo Escaleno: todos os lados e ângulos
são diferentes.

9. • Triângulo Isóceles: dois lados iguais e os
ângulos opostos a esses lados também são
iguais.

10. • Triângulo Equilátero: todos os lados e ângulos
são iguais.

11. Classificação dos Triângulos quanto a
medida de seus ângulos
• Triângulo retângulo: tem um ângulo que
mede 90°.

12. • Triângulo Obtusângulo: tem um ângulo maior
que 90°.

13. • Triângulo Acutângulo: tem todos os ângulos
menores que 90°.

14. Mediana, Bissetriz e Altura de um
Triângulo
• Mediana: Mediana é um segmento que divide
as bases do triângulo em duas partes iguais.

15. • Bissetriz: Bissetriz também é um segmento de reta com
origem em um dos vértices do triângulo com a outra
extremidade no lado oposto a esse vértice. Sendo que ela
divide ao meio o ângulo correspondente ao vértice.

16. • Altura: Encontramos a medida da altura de um
triângulo através de um segmento de reta com
origem em um dos vértices e perpendicular (forma
um ângulo de 90°) ao lado oposto.

17. O Cabri Géomètre
“O Cabri Géomètre permite construir e explorar objetos geométricos
interativamente. Jean- Marie Laborde e Franck Bellemain desenvolveram o
Cabri Géomètre no ”Institut d'Informatique et Mathématiques Appliquées de
Grenoble (IMAG)”, um laboratório de pesquisa da “Université Joseph Fourier”
em Grenoble, França, em cooperação com o “Centre National de la
Recherche Scientifique (CNRS)” e a “Texas Instruments”. ”(Baldin e Villagra,
2002, p. 8).
“Cabri é uma sigla composta pelas iniciais dos termos: CAhier de
BRouillon Interatif. Uma tradução livre é cadernos de rascunhos interativos.
O software é apresentado com um menu e uma lista desdobrável de 11
botões. Esta lista é auto instrutiva, no sentido de auxiliar as tarefas que
executa.” (Sanguino, 2001, apud Becker, 1998 ).

18. Apresentação da Interface do Cabri
• Vídeo 1:
• https://www.youtube.com/watch?
v=lOZXcpQk7Pg

19. Tipos de Triângulos
• Vídeo 2:
• https://www.youtube.com/watch?
v=5RAc8DwmdrE

20. Classificação dos Triângulos quanto a
medida de seus ângulos
• Vídeo 3:
• https://www.youtube.com/watch?
v=_Kitio9Jufs

21. Mediana, Bissetriz e Altura de um
Triângulo
• Vídeo 4:
• https://www.youtube.com/watch?
v=nEiY3G2_Yxs

22. Atividade
1. Construa no Cabri um triângulo:
a. Escaleno;
b. Isóceles;
c. Equilátero.
2. Coloque os valores dos lados e do ângulos de cada
triângulo.
3. Classifique-os quanto a medida de seus ângulos.
4. No primeiro triângulo construído encontre a mediana;
5. No segundo triângulo construído encontre a bissetriz;
6. No terceiro triângulo construído calcule sua altura.
7. Salve sua atividade com seu nome no Cabri e envie ao e-mail
do professor.