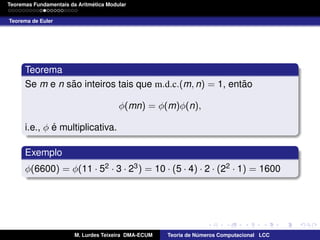
O documento descreve o Teorema de Fermat e o Teorema de Euler, que são fundamentais na teoria da aritmética modular. O Teorema de Fermat estabelece que se p for primo e a qualquer inteiro, então ap ≡ a (mod p). O Teorema de Euler relaciona a função φ de Euler com a congruência modular e estabelece que se a e m forem relativamente primos, então aφ(m) ≡ 1 (mod m). Demonstrações e exemplos são fornecidos.









![´
Teoremas Fundamentais da Aritmetica Modular
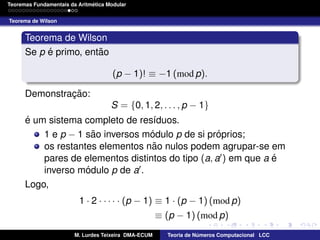
Teorema de Lagrange
Teorema de Lagrange
´
´
Se K e um corpo e f (x) e uma funcao polinomial de grau n em
¸˜
˜
´
K[x], entao a equacao f (x) = 0 tem no maximo n solucoes.
¸˜
¸˜
´
Corolario
´
´
Se p e um primo e f (x) e uma funcao polinomial de grau n de
¸˜
˜
coeficientes inteiros em que nem todos sao divis´veis por p,
ı
˜
ˆ
´
entao a congruencia f (x) ≡ 0 (mod p) tem no maximo n solu´
coes modulo p.
¸˜
´
Corolario
´
˜
ˆ
Se p e um primo e d | p − 1, entao a congruencia
x d − 1 ≡ 0 (mod p)
´
tem exactamente d solucoes modulo p.
¸˜
M. Lurdes Teixeira DMA-ECUM
Teoria de Numeros Computacional LCC
´](https://image.slidesharecdn.com/pequenoteoremadefermat-140225181901-phpapp02/85/Pequeno-teorema-de-fermat-17-320.jpg)