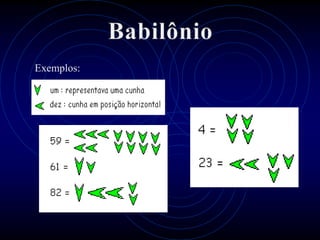
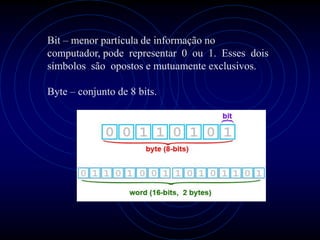
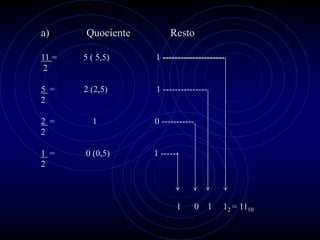
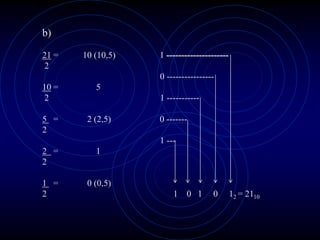
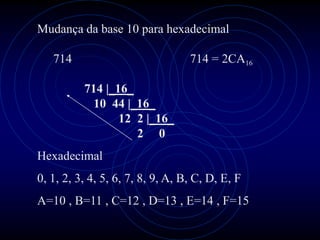
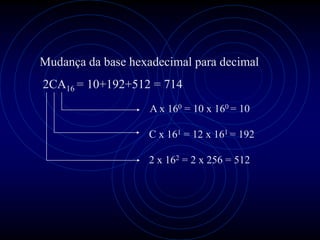
1) O documento discute sistemas de numeração, incluindo os sistemas numéricos egípcio, babilônico, romano, decimal, binário, octal e hexadecimal. 2) Explica que cada sistema tem uma base diferente e como números são representados nessas bases. 3) Detalha como números são convertidos entre as bases binária, decimal, octal e hexadecimal.

1. Instituto Federal de Educação, Ciência e Tecnologia Catarinense
Ana Paula Reinecke¹
Camilla Moreira Uchoa²
Larissa Rozza Peluso³
Disciplina: Arquitetura de Computadores
Professor: Nildo Carlos da Silva
Turma: BSI11

2. Sistemas de Numeração
* Existem várias regras que permitem ler e escrever
qualquer número, usando poucas palavras e poucos
símbolos.
* O conjunto de tais regras constitui um Sistema de
Numeração. Estes sistemas, têm variado com as
épocas e com os povos.

3. Sistemas de Numeração Antigos
Egípcio Babilônio
Romano
1.969 = MCMLXIX

5. Exemplos:

6. Exemplos:

7. Exemplos:
I : um V: cinco X: dez L: cinqüenta
X: cem D: quinhentos M : mil
3 = III 9 = IX 21 = XXI 206 = CCVI
1.969 = MCMLXIX

8. Base de um Sistema
É o número de elementos necessários para formar
um conjunto padrão que auxilie a contagem de
objetos.
Assim, quando falamos em base 10, por exemplo,
estamos pensando na formação de conjuntos com
dez elementos, isto é, dada uma coleção de
objetos, procuramos saber quantos conjuntos de 10
podem ser formados.

9. Bit – menor partícula de informação no
computador, pode representar 0 ou 1. Esses dois
símbolos são opostos e mutuamente exclusivos.
Byte – conjunto de 8 bits.

10. • Existiram e existem diversos sistemas de
numeração.
• No computador, serve para
questões de endereçamento, armazenamento,
conteúdo de tabelas e representações gráficas.
• Bases diferentes usadas nos mais
diversos computadores.

11. Representação nas bases
* 1011012 - 101101 na base 2 (binária)
* 7528 - 752 na base 8 (octal)
* 651 - 651 na base 10 (decimal)
Quando não é indicada a base, a base é
decimal. Mas poderia ser representado assim:
65110
* 42316 - 423 na base 16 (hexadecimal)

12. • Bases
• Binária
• 0, 1
• Octal
• 0, 1, 2, 3, 4, 5, 6, 7
• Decimal
• 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
• Hexadecimal
• 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

13. SISTEMA DECIMAL
Sistema decimal é um sistema de numeração de
base10, com dígitos decimais
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Considere o significado
do número 83. Ele significa oito dezenas e três
unidades:
83 = (8 x 10) + 3
O número 4728 significa quatro milhares, sete
centenas, duas dezenas e oito unidades:
4728 = (4 x 1000) + (7 x 100) + (2 x 10) + 8

14. O sistema decimal é assim chamado por usar a
base 10. Isso significa que cada dígito do
número é multiplicado por 10 elevado à potência
correspondente a posição do dígito:
83 = (8 x 10¹) + (3 x 100)
4728 = (4 x 10³) + (7 x 10²) + (2 x 10¹) + (8 x
100)

15. Valores fracionários são representados do mesmo
modo:
472,83 = (4 x 10²) + (7 x 10¹) + (2 x 10°) + (8 x 10-1)
+ (3 x 10-2)
Em geral, para a representação decimal
de
X = {...x2x1x0 ... x-1x-2x-3...}, o valor de X é igual a:
X= ∑xi10i
i

16. SISTEMA BINÁRIO
No sistema decimal, são usados dez dígitos
distintos para representar os números na base
10. No sistema binário, temos apenas dois
dígitos, 1 e 0. Portanto, números no sistema
binário são representados na base 2.
Para evitar confusão, algumas vezes
usamos um número subscrito para indicar a
base do sistema de numeração adotado. Por
exemplo, 8310 e 4728 10 são números
representados na notação decimal, ou seja,
números decimais.

17. Os dígitos 1 e 0, na notação binária, têm o mesmo
significado que na notação decimal:
02 = 010
12 = 110
Para representar números maiores, como na notação
decimal, cada dígito de um número binário tem um dado
valor, dependendo de sua posição:
10 2 = (1 x 2 1 ) + (0 x 2°) = 2 10
11 2 = (1 x 2 1 ) + (1 x 2°) = 3 10
100 2 = (1 x 2 2) + (0 x 2 1 ) + (0 x 2°) = 4 10
e assim por diante.

18. Valores fracionários são representados com
potências negativas da base:
1001,101 = 2 3 + 2° + 2-1 + 2-3= 9,625 10
CONVERSÃO ENTRE NÚMEROS
BINÁRIOS E DECIMAIS
A conversão de um número na notação
binária para a notação decimal é simples.
Basta multiplicar cada dígito binário pela
potência de 2 adequada e somar os resultados.

19. Para converter a notação decimal em notação binária,
o número inteiro e a parte fracionária são
tratados separadamente. Suponha que queremos
converter um
número inteiro decimal N para a forma binária.
Se dividirmos N por 2, no sistema decimal,
obtendo um quociente N1 e um resto R1, podemos
escrever:
N = 2 x N1 + R1 R1 = 0 ou 1

20. A seguir, dividimos o quociente N1 por 2. Suponha
que o novo quociente seja N2 e o novo resto, R2.
Então:
N1 = 2 x N2 + R2 R2 = 0 ou 1
assim:
N = 2(2N2 + R2) + R1 = 2²N2 + R2 x 2¹ x R1 x 20

21. Se, a seguir, tivermos: N2 = 2N3 + R3
então obteremos:
N= 2³N3 + R3 x 2² + R2 x 2¹ + R1 x 20
Ou seja, podemos converter da base 10 para a base 2
por meio de repetidas divisões por 2. O resto e o
quociente final, 1, nos dão os dígitos binários de N,
na ordem do menor para o maior dígito significativo.
Exemplos de conversão de números inteiros da notação
decimal para a notação binária.

22. a) Quociente Resto
11 = 5 ( 5,5) 1 ---------------------
2
5 = 2 (2,5) 1 ---------------
2
2 = 1 0 -----------
2
1 = 0 (0,5) 1 ------
2
1 0 1 12 = 1110

23. b)
21 = 10 (10,5) 1 ---------------------
2
0 ----------------
10 = 5
2 1 -----------
5 = 2 (2,5) 0 -------
2
1 ---
2 = 1
2
1 = 0 (0,5)
2 1 0 1 0 12 = 2110

24. A conversão da parte fracionária envolve
repetidas multiplicações por dois. A cada passo, a
parte fracionária do número decimal é multiplicada
por 2.
O dígito à esquerda da vírgula decimal no produto
será 0 ou 1 e contribuirá para a representação
binária, começando pelo bit mais significativo. A parte
fracionária do produto é usada como multiplicando
no próximo passo. Para mostrar que isso
funciona, consideramos uma fração decimal
positiva F < 1. Podemos expressar F como:

25. F =(a-1 x 1) + (a-2 x 1) + (a-3 x 1) + ...
2 2² 2³
onde cada a-i é 0 ou 1. Se multiplicarmos isso por
2, teremos:
2F = a-1 + (a-2 x 1) + (a-3 x 1) + (a-4 x 1) + ...
2 2² 2³

26. As partes inteiras dessas duas expressões devem ser
iguais.
Conseqüentemente, a parte inteira de 2F, que deve ser
0 ou 1, uma vez que 0 < F < 1, é simplesmente a-1 .
Portanto:
2F = a-1 + F1 , onde 0 < F1 < 1 e:
F1 =(a-2 x 1) + (a-3 x 1) + (a-4 x 1) + ...
2 2² 2³

27. Para encontrar a-2 repetimos o mesmo processo, que
não é necessariamente exato. Ou seja, uma fração
decimal com um número finito de dígitos pode
demandar uma fração binária com número infinito
de dígitos. Nesses casos, o algoritmo de
conversão normalmente é interrompido depois do
número predefinido de passos, dependendo da
precisão desejada.

28. Representação de binário na base 10
* 11010012
* 11010012 = 1 x 26 + 1 x 25 + 0 x 24 + 1 x 23 +
0 x 22 + 0 x 21 + 1 x 20
* 11010012 = 64 + 32 + 0 + 8 + 0 + 0 + 1
* 11010012 = 10510

29. Representação de octal na base 10
* 546218
* 546218 = 5 x 84 + 4 x 83 + 6 x 82 + 2 x 81 +
1 x 80
* 546218 = 20480 + 2048 + 384 + 16 + 1
* 546218 = 2292910

30. Representação de hexadecimal na base 10
* 3974116
* 3974116 = 3 x 164 + 9 x 163 + 7 x 162 + 4 x 161 +
1 x 160
* 3974116 = 196608 + 36864 + 1792 + 64 + 1
* 3974116 = 23532910

31. NOTAÇÃO HEXADECIMAL
Em virtude da natureza binária inerente dos
componentes de um computador digital, todas as
formas de dados são representadas, dentro do
computador, por códigos binários.
No entanto, embora o sistema binário seja
conveniente para computadores, é excessivamente
ineficiente para seres humanos. Por isso, a
maioria dos profissionais de computação que
passam grande parte do tempo trabalhando
com dados manipulados no computador
prefere uma notação mais compacta.

32. Exemplos de conversão de números fracionários da
notação decimal para a notação binária.
a) 0,8110 = 0,1100112 (aproximado)
Produto Parte inteira , 1 1 0 0 1 1
0,81 x 2 = 1,62 1 ------
0,62 x 2 = 1,24 1 ---------
0,24 x 2 = 0,48 0 ------------
0,48 x 2 = 0,96 0 ---------------
0,96 x 2 = 1,92 1 ------------------
0,92 x 2 = 1,84 1 ---------------------

33. b) 0,2510 = 0,012 (exato)
,0 1
0,25 x 2 = 0,5 0 ------------------
0,5 x 2 = 1,0 1 ---------------------
Em vez disso, é adotada uma notação conhecida como
hexadecimal. Os dígitos binários são agrupados em
conjuntos de quatro. A cada combinação possível de
quatro dígitos binários é atribuído um símbolo, como a
seguir:

34. 0000 = 0 1000 = 8
0001 = 1 1001 = 9
0010 = 2 1010 = A
0011 = 3 1011 = B
0100 = 4 1100 = C
0101 = 5 1101 = D
0110 = 6 1110 = E
0111 = 7 1111 = F
Por serem usados 16 símbolos, a notação é chamada
hexadecimal e esses 16 símbolos são os dígitos
hexadecimais.

35. Uma seqüência de dígitos hexadecimais pode ser vista
como uma representação de um número inteiro na base 16.
Portanto,
1A16 = (116 x 16¹) + (A16 x 16 0)
= (110 x 16¹) + (1010 x 16 0) = 26
A notação hexadecimal é usada não apenas para representar
números inteiros. Ela também é usada como uma notação
concisa para representar qualquer seqüência de dígitos
binários, mesmo que representem texto, números ou algum
outro tipo de dado. As razões para se usar notação
hexadecimal são as seguintes:

36. 1. É mais compacta que a notação binária.
2. Na maioria dos computadores, os dados binários
têm um tamanho que é múltiplo de 4 bits e, portanto,
múltiplo de um dígito hexadecimal.
3. É extremamente fácil converter entre as
notações binária e hexadecimal.
Como um exemplo desse último ponto, considere
a seqüência de bits 110111100001. Isso é equivalente a:
1101 1110 0001 = DE116
D E 1

37. Esse processo é realizado tão naturalmente que um
programador experiente pode converter representações
visuais de dados binários para seus equivalentes
hexadecimais mentalmente, sem precisar escrever.

38. Mudança da base 10 para binário
714
714 |_2_
0 357 |_2_
1 178 |_2_ 714 = 10110010102
0 89 |_2_
1 44 |_2_
0 22 |_2_
0 11 |_2_
1 5 |_2_
1 2 |_2_
0 1 |_2_
1 0

39. Mudança da base 10 para octal
714 714 = 13128
714 |_8_
2 89 |_8_
1 11 |_8_
3 1 |_8_
1 0

40. Mudança da base 10 para hexadecimal
714 714 = 2CA16
714 |_16_
10 44 |_16_
12 2 |_16_
2 0
Hexadecimal
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
A=10 , B=11 , C=12 , D=13 , E=14 , F=15

41. Mudança da base octal para decimal (10)
13128 = 2+8+192+512 = 714
2 x 80 = 2
1 x 81 = 8
3 x 82 = 192
1 x 83 = 512

42. Mudança da base hexadecimal para decimal
2CA16 = 10+192+512 = 714
A x 160 = 10 x 160 = 10
C x 161 = 12 x 161 = 192
2 x 162 = 2 x 256 = 512

43. ARITMÉTICA COMPUTACIONAL
As palavras de um computador são compostas por bits e
podem representar números armazenados na memória.
Estes números podem ter diferentes significados, como
inteiros ou reais, serem positivos ou negativos.
A manipulação dos números inclui operações de soma,
subtração, multiplicação e divisão.

44. COMPLEMENTO DE 1 (C – 1)
Este sistema de representação também utiliza o bit mais
à esquerda para o sinal, correspondendo o 0 ao sinal + e
o 1 ao sinal -. Para os números positivos, os N- 1 bits da
direita representam o módulo. O simétrico de um número
positivo é obtido pelo complemento de todos os seus dígitos
(trocando 0 por 1 e vice-versa) incluindo o bit de sinal.

45. Exemplo: representar 10 e –10
Limitação de 8 bits (N=8)
10 0 0001010
Nº sinal módulo
Número – 10 é o complemento do seu simétrico
-10 1 1110101
Nº sinal módulo

46. Vantagem: possuir faixa simétrica.
Inconveniência: 2 representações para o número 0.
Para 8 bits o 0 tem as seguintes representações:
00000000 (+0)
10000000 (-0)

47. Complemento de 1 com valores inteiros de 4 bits
Decimal Complemento de 1
0 0000 −0 1111
1 0001 −1 1110
2 0010 −2 1101
3 0011 −3 1100
4 0100 −4 1011
5 0101 −5 1010
6 0110 −6 1001
7 0111 −7 1000

48. COMPLEMENTO DE 2 ( C – 2)
Este sistema de representação utiliza o bit mais à esquerda
para o sinal, correspondendo o 0 ao sinal + e o 1 ao sinal -.
Para os números positivos, os N- 1 bits da direita
representam o módulo, igualmente ao MS (módulo e sinal)
e C - 1.
O simétrico de um número é obtido em dois passos: 1º
passo – obtém-se o complemento de todos os bits do
número positivo (trocando 0 por 1 e vice-versa) incluindo o
bit de sinal, isto é, executa-se o complemento de 1;
2º passo – ao resultado obtido no primeiro passo, soma-se
1 (em binário).

49. Exemplo: complemento de 2 dos números 10 e –10
Limitação de 8 bits (N=8)
10 0 0001010
nº sinal módulo

50. Número – 10
1º passo: complemento de 1
-10 1 1110101
nº sinal módulo
2º passo: 1
1110101
+ 10
-----------
1110110

51. Vantagem: uma única representação para o número 0..
Para 8 bits teremos:
Nº 0 00000000 (+0)
Nº -0 passo 1 11111111 (-0)
passo 2 1
-------------------
100000000
estouro desprezado
Logo 0 e –0 tem a mesma representação.

52. OPERAÇÕES COM NÚMEROS BINÁRIOS
Adição
A adição no sistema binário é realizada exatamente da
mesma forma que uma adição no sistema decimal.
Vamos inicialmente realizar uma adição na base 10 e
posteriormente outra na base 2.
Seja a operação 85 + 18.
85
18 +
-----
103

53. -Somamos por colunas à partir da direita, temos
8+5=13, como a soma excedeu o maior dígito
disponível, usamos a regra do transporte para a
próxima coluna.
- Assim, dizemos que dá 3 e “vai um”.
- Este transporte “vai um” é computado na soma da
próxima coluna, que passa a ser 8+1+1=10, novamente
usamos o transporte e dizemos que dá 0 e “vai um”
abrindo uma nova coluna que é 0+0+1=1.
- Obtemos desta forma o resultado 103.

54. -- Vamos agora para o sistema base 2, como temos
apenas dois dígitos, vamos verificar quais os possíveis
casos que ocorrerão na soma por colunas:
-a) 0 b)0 c)1 d)1 e)1
+0 +1 +0 +1 1
---- ---- ---- ---- +1
0 1 1 10 ----
11
- No caso “d” houve transporte, o resultado é 0 e “vai
um” e no caso “e” realizamos a soma de três parcelas
incluindo um transporte, o resultado é 1 e “vai um”.

55. Subtração
-Como o método também é análogo ao da subtração no sistema
decimal, vamos ver quais os possíveis casos que ocorrerão na
subtração por colunas.
a) 0 b) 0 c) 1 d) 1
-0 -1 -0 -1
---- ---- ---- ----
0 1 1 0

56. - No caso “b”, o resultado será 1, mas ocorrerá um
transporte para a coluna seguinte, que deve ser
acumulado no subtraendo. Exemplificando, vamos
efetuar 11102 – 10012
1110
-1001
-------
0101

57. Multiplicação
-Novamente análoga ao caso decimal. Agora os casos
possíveis são:
a) 0x0 = 0 b) 0x1 = 0 c) 1x0 = 0 e d) 1x1 = 1
A multiplicação de números binários é feita do
mesmo modo que a multiplicação de números decimais.

58. O procedimento, na verdade, é mais simples, uma vez
que os dígitos multiplicadores podem ser apenas 0 ou
1.
O exemplo seguinte ilustra este procedimento para
números binários sem sinal.
1001
1011
-----------
1001
1001
0000
1001
1100011

59. Caso um número esteja em complemento de 2, deve-
se primeiro convertê-lo para o seu equivalente em
binário positivo. Assim, é possível efetuar a
multiplicação como no caso acima.Evidente que o
resultado deve ser convertido para binário
negativo, usando o complemento de 2.

60. Divisão Binária
O processo para dividir números binários é o mesmo
que é utilizado para números decimais.Para ilustrar,
segue um exemplo onde iremos dividir (9) 10 por (3) 10.
+9 = 1 0 0 1
+3 = 1 1

61. 1 0 0 1 /1 1
1 1 1 1(3) 10
---------
0011
11
----------
0
A divisão de números com sinal é tratada do
mesmo modo que na multiplicação.