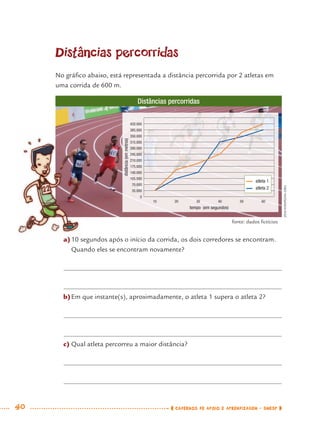
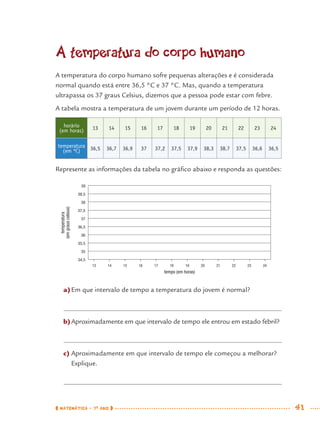
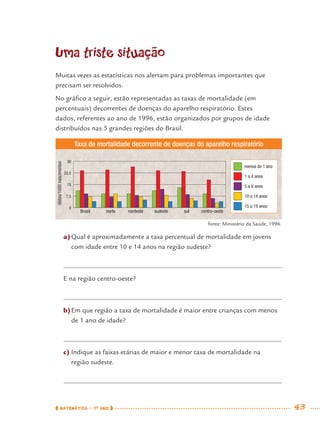
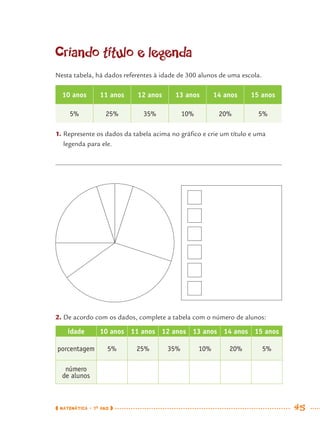
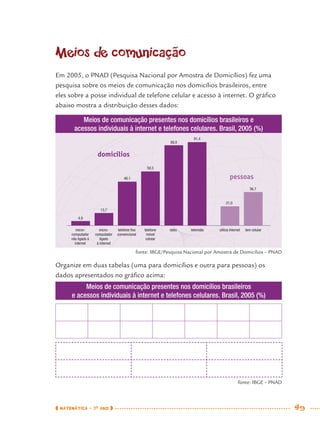
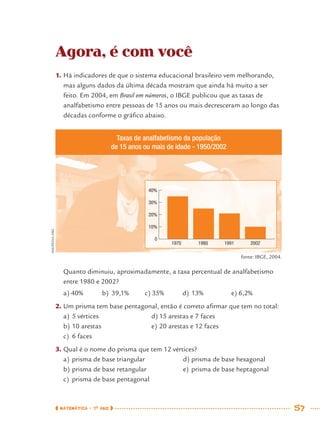
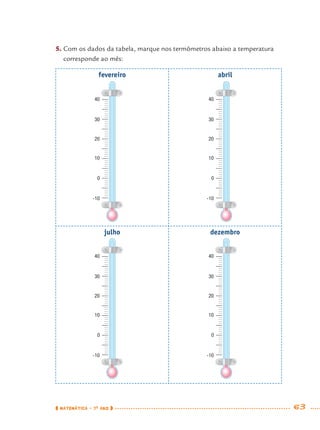
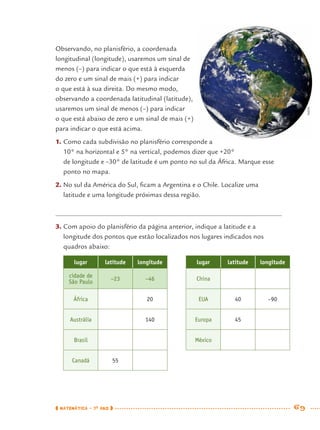
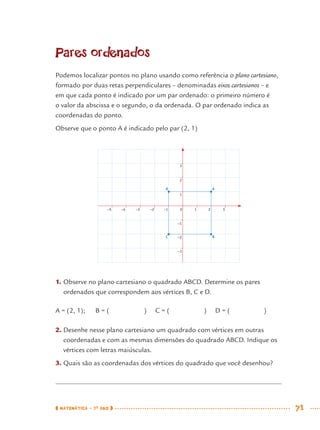
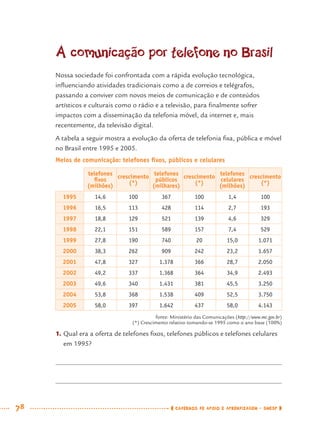
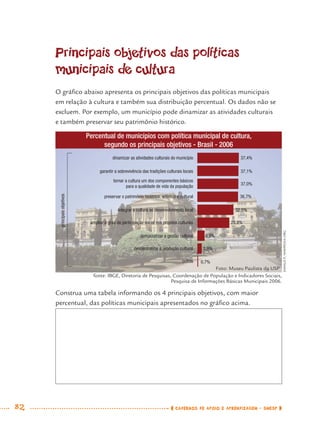
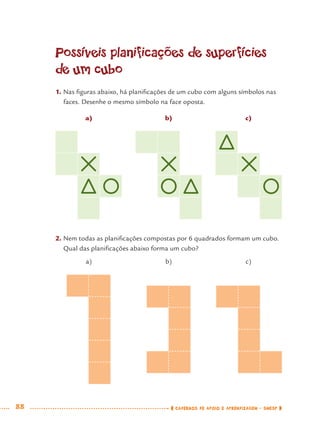
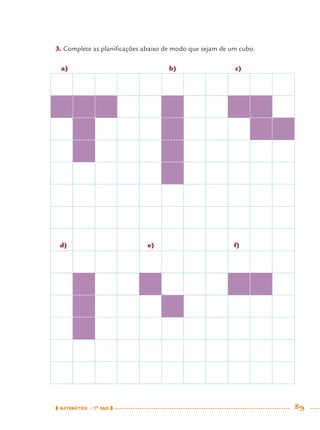
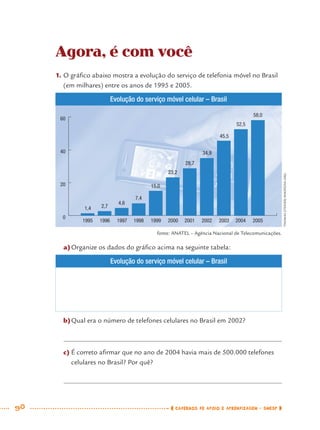
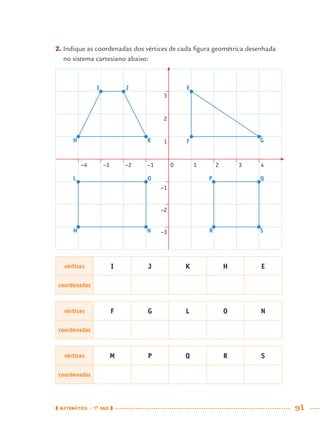
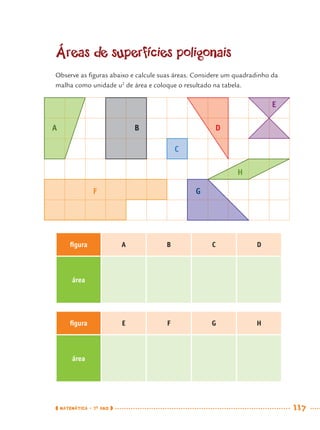
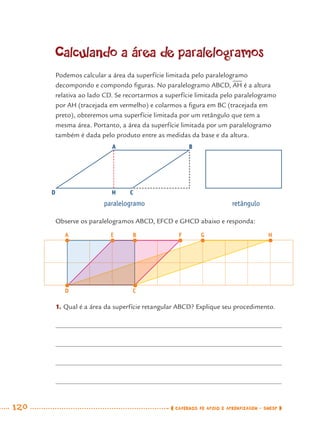
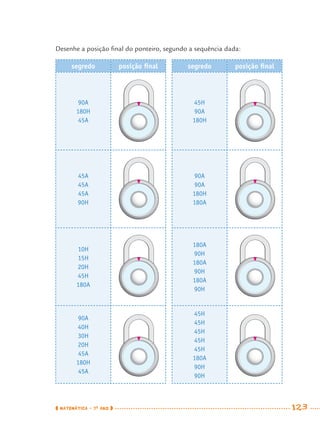
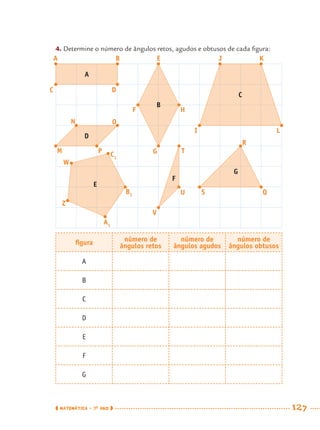
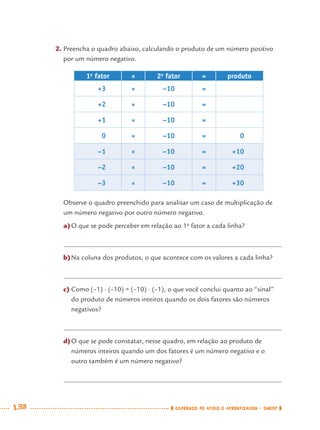
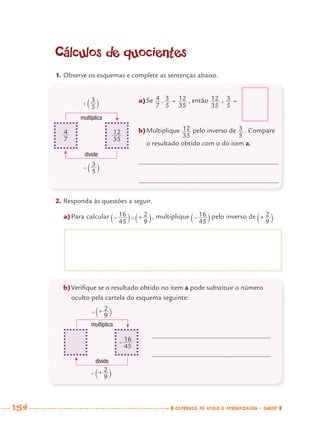
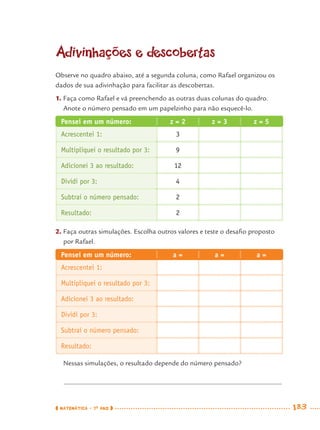
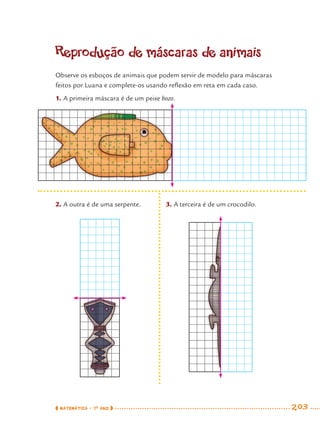
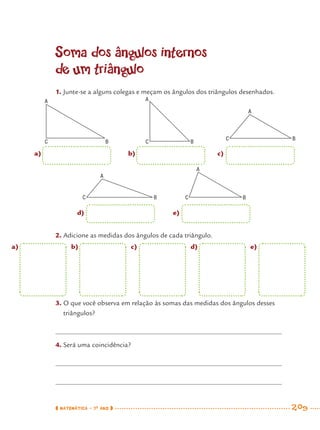
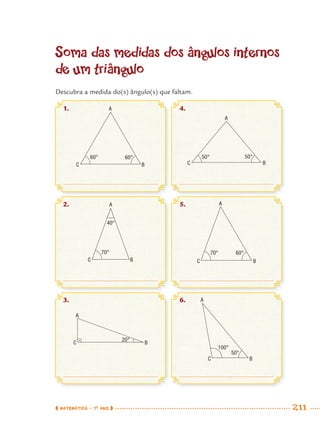
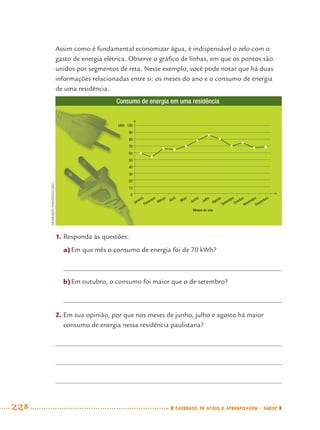
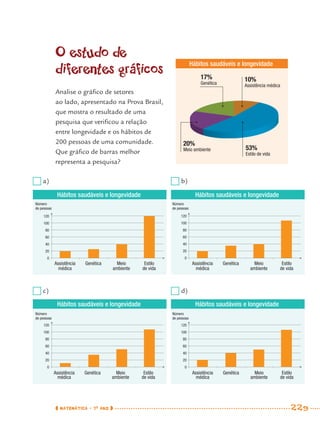
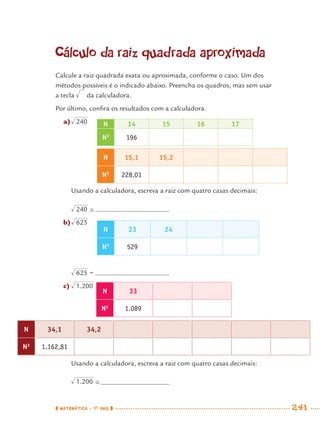
1) Este documento apresenta um caderno de apoio e aprendizagem para matemática do 7o ano do ensino fundamental. 2) Ele foi produzido pela Secretaria Municipal de Educação de São Paulo com o objetivo de auxiliar os alunos em suas atividades de aprendizagem. 3) O caderno contém diversas atividades e exercícios sobre diferentes temas matemáticos para serem resolvidos pelos alunos com o apoio do professor.