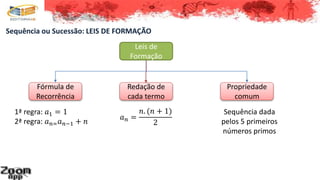
Este documento discute sequências numéricas e suas propriedades. Ele define o que é uma sequência numérica e explica os conceitos de termos, finitude vs infinitude. Também discute progressões aritméticas e geométricas, definindo suas razões e termos gerais, e fornece exemplos de cálculos com essas sequências.

1. Matemática
Sequências Numéricas

2. Sequências Numéricas:
1. Sequências Numéricas;
a. Sequência ou Sucessão;
b. Leis de Formação;
2. Progressão Aritmética;
a. Condição de Existência;
b. Razão “r”;
c. Termo Geral;
d. Propriedades de uma PA;
e. Interpolação;
f. Soma dos n primeiros termos de uma PA;
3. Progressão Geométrica;
a. Condição de Existência;
b. Razão “q”;
c. Termo Geral;
d. Propriedades de uma PG;
e. Interpolação;
f. Soma dos n primeiros termos de uma PG;
g. Soma dos Infinitos termos de uma PG.

3. Sequência – Chama-se sequência toda função 𝒇 𝒅𝒆 𝒅𝒐𝒎í𝒏𝒊𝒐 𝑨 ∖ 𝑨 ⊂
ℕ∗ 𝒆 𝒄𝒐𝒏𝒕𝒓𝒂𝒅𝒐𝒎í𝒏𝒊𝒐 𝑩, 𝒔𝒆𝒏𝒅𝒐 𝑩 𝒖𝒎 𝒄𝒐𝒏𝒋𝒖𝒏𝒕𝒐 𝒏ã𝒐 𝒗𝒂𝒛𝒊𝒐.
Sequência ou Sucessão: CONCEITOS
.1º
.2º
.3º
.4º
...
.1200
.1400
.1600
.2200
...
Exemplo: Percurso percorrido em metros por um iniciante de um treinamento
de corrida por cada dia de treino.
Dia Distância (m)

4. 1) Pode ser representada apenas pela imagem da função;
1200m, 1400m, 1600m, 2200m ...
2) Cada elemento é denominado TERMO da sequência. O primeiro elemento é chamado de
primeiro termo e é indicado por 𝑎1, assim sucessivamente até o enésimo termo
denominado 𝑎 𝑛;
3) A notação matemática de uma sequência será: 𝑔 = 𝑎𝑖 𝑖 ∈ ℕ∗
;
4) As sequências podem ser Finitas ou Infinitas de acordo com a quantidade definível de
elementos;
Sequência ou Sucessão: CARACTERÍSTICAS

5. Sequência ou Sucessão: LEIS DE FORMAÇÃO
Leis de
Formação
Fórmula de
Recorrência
Redação de
cada termo
Propriedade
comum
1ª regra: 𝑎1 = 1
2ª regra: 𝑎 𝑛= 𝑎 𝑛−1 + 𝑛
𝑎 𝑛 =
𝑛. (𝑛 + 1)
2
Sequência dada
pelos 5 primeiros
números primos

6. Fim da Apresentação.