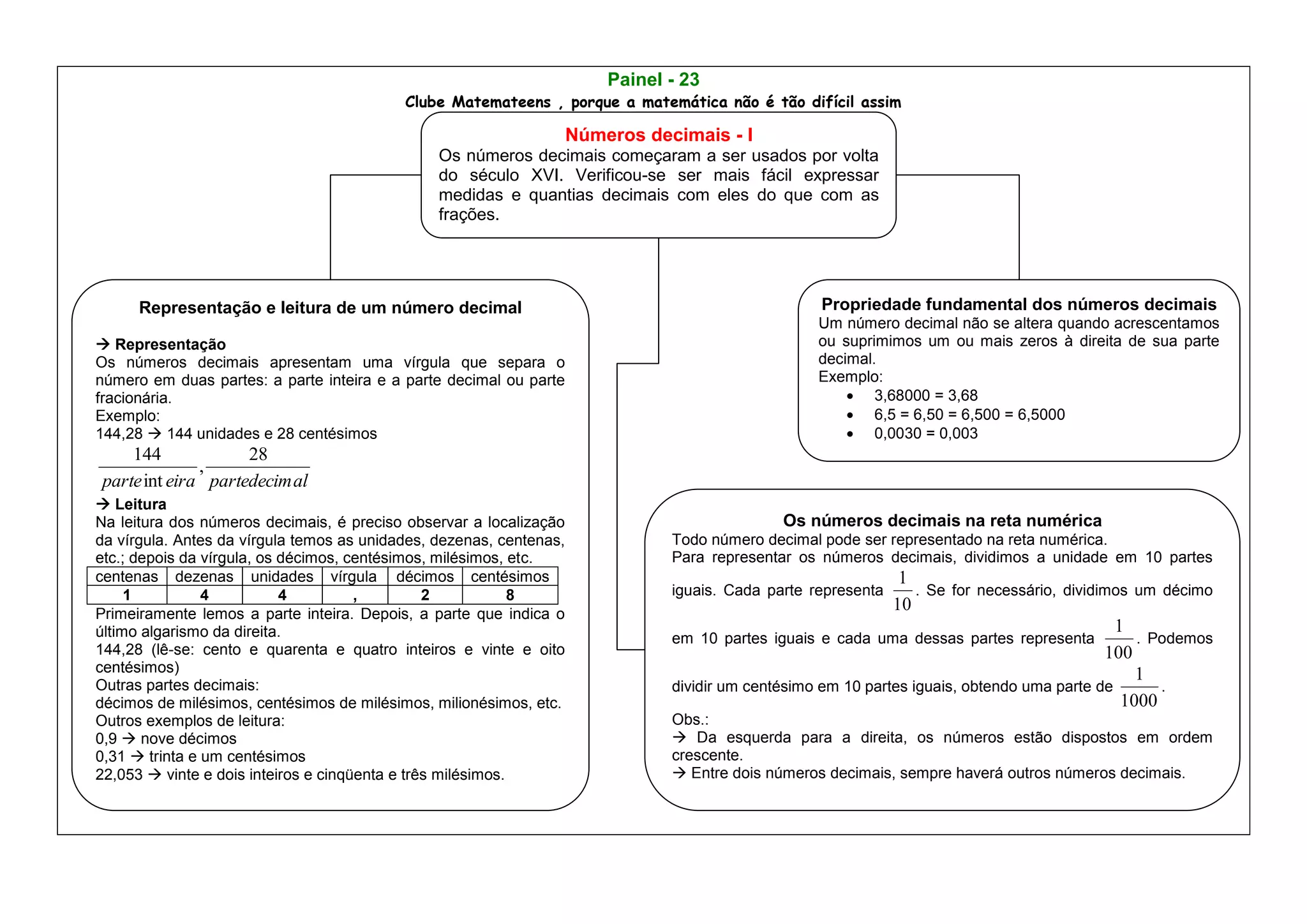
O documento apresenta os números decimais, explicando sua representação com vírgula para separar a parte inteira da decimal. Também mostra que acrescentar ou remover zeros à direita não altera o valor, e como representá-los na reta numérica dividindo cada parte decimal em dez partes iguais.

1. Painel - 23
Clube Matemateens , porque a matemática não é tão difícil assim
Números decimais - I
Os números decimais começaram a ser usados por volta
do século XVI. Verificou-se ser mais fácil expressar
medidas e quantias decimais com eles do que com as
frações.
Representação e leitura de um número decimal Propriedade fundamental dos números decimais
Um número decimal não se altera quando acrescentamos
 Representação ou suprimimos um ou mais zeros à direita de sua parte
Os números decimais apresentam uma vírgula que separa o decimal.
número em duas partes: a parte inteira e a parte decimal ou parte Exemplo:
fracionária.  3,68000 = 3,68
Exemplo:  6,5 = 6,50 = 6,500 = 6,5000
144,28  144 unidades e 28 centésimos  0,0030 = 0,003
144 28
,
parte int eira partedecim al
 Leitura
Na leitura dos números decimais, é preciso observar a localização Os números decimais na reta numérica
da vírgula. Antes da vírgula temos as unidades, dezenas, centenas, Todo número decimal pode ser representado na reta numérica.
etc.; depois da vírgula, os décimos, centésimos, milésimos, etc. Para representar os números decimais, dividimos a unidade em 10 partes
centenas dezenas unidades vírgula décimos centésimos 1
1 4 4 , 2 8 iguais. Cada parte representa . Se for necessário, dividimos um décimo
Primeiramente lemos a parte inteira. Depois, a parte que indica o
10
último algarismo da direita. 1
em 10 partes iguais e cada uma dessas partes representa . Podemos
144,28 (lê-se: cento e quarenta e quatro inteiros e vinte e oito 100
centésimos) 1
Outras partes decimais: dividir um centésimo em 10 partes iguais, obtendo uma parte de .
décimos de milésimos, centésimos de milésimos, milionésimos, etc. 1000
Outros exemplos de leitura: Obs.:
0,9  nove décimos  Da esquerda para a direita, os números estão dispostos em ordem
0,31  trinta e um centésimos crescente.
22,053  vinte e dois inteiros e cinqüenta e três milésimos.  Entre dois números decimais, sempre haverá outros números decimais.