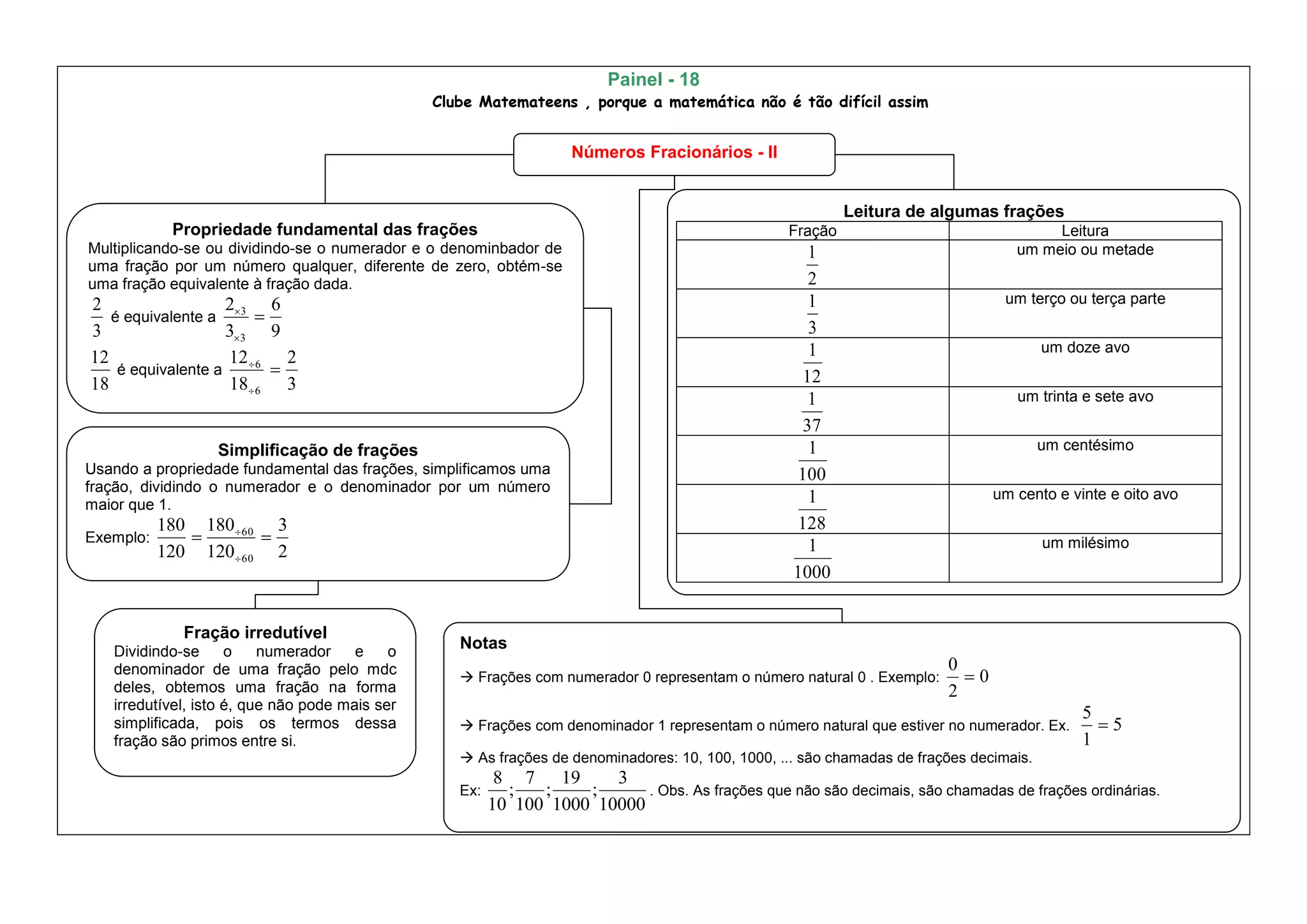
1) O documento discute propriedades fundamentais de frações, incluindo como frações equivalentes podem ser obtidas multiplicando ou dividindo o numerador e denominador por um número. 2) Ele também explica como simplificar frações dividindo o numerador e denominador por seu maior divisor comum. 3) Por fim, o documento fornece exemplos de leituras comuns de frações e notas sobre frações com numerador 0, denominador 1 e frações decimais versus frações ordinárias.

1. Painel - 18
Clube Matemateens , porque a matemática não é tão difícil assim
Números Fracionários - II
Leitura de algumas frações
Propriedade fundamental das frações Fração Leitura
Multiplicando-se ou dividindo-se o numerador e o denominbador de 1 um meio ou metade
uma fração por um número qualquer, diferente de zero, obtém-se
uma fração equivalente à fração dada. 2
2 2 6 1 um terço ou terça parte
é equivalente a 3 
3 33 9 3
1 um doze avo
12 12  6 2
é equivalente a  12
18 18 6 3
1 um trinta e sete avo
37
Simplificação de frações 1 um centésimo
Usando a propriedade fundamental das frações, simplificamos uma 100
fração, dividindo o numerador e o denominador por um número um cento e vinte e oito avo
maior que 1. 1
180 180 60 3 128
Exemplo:   1 um milésimo
120 120 60 2
1000
Fração irredutível
Dividindo-se o numerador e o
Notas
denominador de uma fração pelo mdc 0
 Frações com numerador 0 representam o número natural 0 . Exemplo: 0
deles, obtemos uma fração na forma 2
irredutível, isto é, que não pode mais ser
5
simplificada, pois os termos dessa  Frações com denominador 1 representam o número natural que estiver no numerador. Ex. 5
fração são primos entre si. 1
 As frações de denominadores: 10, 100, 1000, ... são chamadas de frações decimais.
8 7 19 3
Ex: ; ; ; . Obs. As frações que não são decimais, são chamadas de frações ordinárias.
10 100 1000 10000