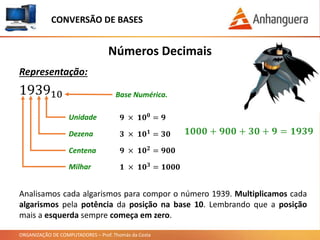
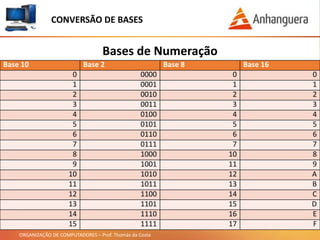
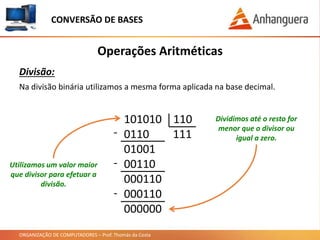
Este documento discute conversão de bases numéricas e operações aritméticas em binário. Ele explica como representar números na base decimal e em outras bases como binário, octal e hexadecimal. Também mostra como converter entre diferentes bases usando uma fórmula e dividindo números. Por fim, demonstra como realizar soma, subtração, multiplicação e divisão em binário usando tabelas de verdade.

1. ANHANGUERA – 2016.2
ORGANIZAÇÃO DE COMPUTADORES
AULA 03 – CONVERSÃO DE BASES
Prof. Thomás da Costa
thomascosta@aedu.com

2. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
CONVERSÃO DE BASES
CONVERSÃO DE BASES

3. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Números Decimais
Notação:
• É de conhecimento geral, que os números e suas operações matemáticas
são de extrema importância para o nosso dia-a-dia.
• Em nossas vidas, conhecemos o sistema de notação decimal.
• O sistema de notação decimal possui essa denominação, devido a sua faixa
de números que contém dez diferentes algarismos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
• Podemos representar o número 1939 identificando a base 𝟏𝟗𝟑𝟗 𝟏𝟎, mas
normalmente não utilizamos este tipo de representação diariamente.
• Além disso nosso sistema numérico é posicional, onde cada algarismo
possui uma representação (unidade, centena, dezena e milhar).
CONVERSÃO DE BASES
Vamos analisar o número 1939 !!!

4. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Números Decimais
CONVERSÃO DE BASES
Representação:
Unidade
Dezena
Centena
Milhar
𝟗 × 𝟏𝟎 𝟎 = 𝟗
𝟑 × 𝟏𝟎 𝟏 = 𝟑𝟎
𝟗 × 𝟏𝟎 𝟐
= 𝟗𝟎𝟎
𝟏 × 𝟏𝟎 𝟑 = 𝟏𝟎𝟎𝟎
𝟏𝟎𝟎𝟎 + 𝟗𝟎𝟎 + 𝟑𝟎 + 𝟗 = 𝟏𝟗𝟑𝟗
193910 Base Numérica.
Analisamos cada algarismos para compor o número 1939. Multiplicamos cada
algarismos pela potência da posição na base 10. Lembrando que a posição
mais a esquerda sempre começa em zero.

5. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Bases de Numeração
Detalhes:
• Efetuando uma comparação com a base decimal que possui 10 números,
podemos representar uma outra base de acordo com a quantidade de
números.
• Por exemplo a base 5, possui os números 0, 1, 2, 3, 4.
• A base 8, possui os números 0, 1, 2, 3, 4, 5, 6, 7.
• As bases mais utilizadas são 2, 8, 10 e 16.
• Bases maiores que 10 utilizam-se letras do alfabeto para os algarismos.
• Em um sistema computacional, os números são representados na base 2.
• A base 2 possui somente dois números 0 e 1.
• Estes números são conhecidos como bits.
• A representação da base 2 é conhecida como base binária ou sistema
binário.
CONVERSÃO DE BASES

6. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Bases de Numeração
CONVERSÃO DE BASES
Base 10 Base 2 Base 8 Base 16
0 0000 0 0
1 0001 1 1
2 0010 2 2
3 0011 3 3
4 0100 4 4
5 0101 5 5
6 0110 6 6
7 0111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F

7. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Bases de Numeração
Como contar em uma base 2, 8 ou 16:
• Contar na base decimal é a forma mais natural que conhecemos.
• Mas como contar por exemplo na base 8? Vamos ver um exemplo
comparando com a base 10.
Contando na Base 10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 próximo número seria o 10.
Por que? Simplesmente porque estamos no fim de uma unidade e iniciando
uma nova dezena. Isso acontece para as outras bases.
Contando na Base 8: 0, 1, 2, 3, 4, 5, 6, 7 próximo número seria o 10. Seguindo a
mesma lógica utilizada na base 10.
CONVERSÃO DE BASES

8. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Conversão
Base B para Base 10:
Para efetuar a conversão de uma base qualquer para a base decimal, podemos
utilizar a seguinte formula:
CONVERSÃO DE BASES
𝑵 = 𝒅 𝒏−𝟏 × 𝒃 𝒏−𝟏 + 𝒅 𝒏−𝟐 × 𝒃 𝒏−𝟐 + … + 𝒅 𝟏 × 𝒃 𝟏 + 𝒅 𝟎 × 𝒃 𝟎
Onde:
d = indica cada algarismo do número.
n – 1, n – 2, 1, 0 = indicam a posição de cada algarismo.
b = indica a base de numeração.
n = indica o número de dígitos.
Vamos analisar um exemplo.

9. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Conversão
Base 2 para Base 10:
(𝟏𝟎𝟏𝟏𝟎𝟏) 𝟐 = ( ) 𝟏𝟎
b = 2
n = 6
d = representa cada algarismo do número binário.
CONVERSÃO DE BASES
𝑵 = 𝒅 𝒏−𝟏 × 𝒃 𝒏−𝟏 + 𝒅 𝒏−𝟐 × 𝒃 𝒏−𝟐 + … + 𝒅 𝟏 × 𝒃 𝟏 + 𝒅 𝟎 × 𝒃 𝟎
𝑵 = 𝟏 × 𝟐 𝟓 + 𝟎 × 𝟐 𝟒 + 𝟏 × 𝟐 𝟑 + 𝟏 × 𝟐 𝟐 + 𝟎 × 𝟐 𝟏 + 𝟏 × 𝟐 𝟎
𝑵 = 𝟏 × 𝟑𝟐 + 𝟎 × 𝟏𝟔 + 𝟏 × 𝟖 + 𝟏 × 𝟒 + 𝟎 × 𝟐 + 𝟏 × 𝟏
𝑵 = 𝟑𝟐 + 𝟎 + 𝟖 + 𝟒 + 𝟎 + 𝟏
𝑵 = 𝟒𝟓 𝟏𝟎

10. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Conversão
Exercícios:
CONVERSÃO DE BASES
Efetuar as seguintes conversões:
1) (27)8 = ( )10
2) (2𝐴5)16 = ( )10
3) (6734)8 = ( )10
4) (457)9 = ( )10
5) (243)5 = ( )10
Respostas:
1) (27)8 = (23)10
2) (2𝐴5)16 = (677)10
3) (6734)8 = (3548)10
4) (457)9 = (376)10
5) (243)5 = (73)10

11. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Conversão
Base 2 para Base 8, 16:
CONVERSÃO DE BASES
Como 8 = 23 e 16 = 24 podemos efetuar as conversões utilizando grupos de
3 e 4 bits respectivamente e substituindo pelo seu equivalente na base.
Base 2 para Base 8:
(𝟏𝟏𝟏𝟎𝟏𝟎𝟏𝟏𝟏) 𝟐 = (𝟕𝟐𝟕) 𝟖
(111) = 7
(010) = 2
(111) = 7
Base 2 para Base 16:
(𝟏𝟎𝟏𝟏𝟎𝟏𝟏𝟎𝟏𝟏) 𝟐 = (𝟐𝑫𝑩) 𝟏𝟔
(0010) = 2
(1101) = D
(1011) = B
Podemos efetuar o processo de conversão da base 8 e 16 para 2, convertendo
cada algarismos do número para seu valor correspondente em binário.

12. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Conversão
Exercícios:
CONVERSÃO DE BASES
Efetuar as seguintes conversões:
1) (1010011111)2 = ( )8
2) (327)8 = ( )2
3) (306)16 = ( )2
4) (𝐹50)16 = ( )2
5) (10011100101101)2 = ( )16
Respostas:
1) (1010011111)2 = (1237)8
2) (327)8 = (11010111)2
3) (306)16 = (1100000110)2
4) (𝐹50)16 = (111101010000)2
5) (10011100101101)2 = (272D)16

13. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Conversão
Base 10 para Base B:
• Para efetuar a conversão, precisamos dividir o número na base 10 pelo valor
da base a ser convertida e utilizar o resto da divisão como algarismo do
número resultante.
• Devemos efetuar essa operação até o quociente for diferente de zero ou o
dividendo for maior que o divisor.
CONVERSÃO DE BASES
Base 10 para Base 8:
(𝟑𝟗𝟔𝟒) 𝟏𝟎 = (𝟕𝟓𝟕𝟒) 𝟖
3964/8 = 495 𝑟𝑒𝑠𝑡𝑜0 = 4
495/8 = 61 𝑟𝑒𝑠𝑡𝑜1 = 7
61/8 = 7 𝑟𝑒𝑠𝑡𝑜2 = 5
7/8 = 0 𝑟𝑒𝑠𝑡𝑜3 = 7
Base 10 para Base 16:
(𝟐𝟕𝟓𝟒) 𝟏𝟎 = (𝑨𝑪𝟐) 𝟏𝟔
2754/16 = 172 𝑟𝑒𝑠𝑡𝑜0 = 2
172/16 = 10 𝑟𝑒𝑠𝑡𝑜1 = 12
10/16 = 0 𝑟𝑒𝑠𝑡𝑜2 = 10

14. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Conversão
Exercícios:
CONVERSÃO DE BASES
Efetuar as seguintes conversões:
1) (45)10 = ( )2
2) (97)10 = ( )2
3) (490)10 = ( )16
4) (483)10 = ( )8
5) (3964)10 = ( )8
Respostas:
1) (45)10 = (101101)2
2) (97)10 = (1100001)2
3) (490)10 = (1EA)16
4) (483)10 = (743)8
5) (3964)10 = (7574)8

15. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Operações Aritméticas
Detalhes:
• No sistema decimal efetuamos operações aritméticas para as mais diversas
finalidades.
• As operações aritméticas fundamentais são a soma, subtração,
multiplicação e divisão.
• Podemos efetuar as mesmas operações aritméticas em outras bases.
• Vamos aprender a somar, subtrair, multiplicar e dividir na base 2.
CONVERSÃO DE BASES

16. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Operações Aritméticas
Soma:
Como na base 2 existe somente dois algarismos, podemos criar uma tabela
com todas as possibilidades:
CONVERSÃO DE BASES
0 + 0 = 0 0 + 1 = 1
1 + 0 = 1 1 + 1 = 0 com “vai 1” ou 102
101101
101111
1011100
Exemplo:
+
1 1111
“Vai 1” ou 𝟏𝟎 𝟐

17. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Operações Aritméticas
Subtração:
Como na base 2 existe somente dois algarismos, podemos criar uma tabela
com todas as possibilidades:
CONVERSÃO DE BASES
0 - 0 = 0 0 - 1 = “empresta 1” da casa a esquerda
com valor 1
1 - 0 = 1 1 - 1 = 0
101101
100111
000110
Exemplo:
-
2
002
“empresta 1”
Quando acontece o
“empresta 1” o número
vira 𝟏𝟎 𝟐 que equivale ao
numero 𝟐 𝟏𝟎
OBS: Quando se subtrai um
número menor por um maior,
realizamos a operação normal e
invertemos o sinal.

18. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Operações Aritméticas
Multiplicação:
Como na base 2 existe somente dois algarismos, podemos criar uma tabela
com todas as possibilidades:
CONVERSÃO DE BASES
0 X 0 = 0 0 X 1 = 0
1 X 0 = 0 1 x 1 = 1
110
101
110
000
110
11110
Exemplo:
X
Para cada algarismos,
deslocar uma casa para
a esquerda.
Multiplica todas as casas.
Soma as multiplicações e
obtemos o resultado.
+

19. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Operações Aritméticas
Divisão:
Na divisão binária utilizamos a mesma forma aplicada na base decimal.
CONVERSÃO DE BASES
101010 110
0110 111
01001
00110
000110
000110
000000
-
-
-
Utilizamos um valor maior
que divisor para efetuar a
divisão.
Dividimos até o resto for
menor que o divisor ou
igual a zero.

20. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Operações Aritméticas
Exercícios:
CONVERSÃO DE BASES
Efetuar as seguintes operações:
1) (11011 + 11001)2 = ( )2
2) (101100101 + 100111011)2 = ( )2
3) (100101 − 011010)2 = ( )2
4) (10010 × 100)2 = ( )2
5) (101010 ÷ 110)2 = ( )2
Respostas:
1) (11011 + 11001)2 = (110100)2
2) (101100101 + 100111011)2 = (1010100000)2
3) (100101 − 11010)2 = (1011)2
4) (10010 × 100)2 = (1001000)2
5) (101010 ÷ 110)2 = (111)2

21. ORGANIZAÇÃO DE COMPUTADORES – Prof. Thomás da Costa
Resumo
CONVERSÃO DE BASES
• Existem outras bases numéricas além da base decimal.
• As mais utilizadas são a base 2, 8, 10 e 16.
• A base 2 é conhecida como a base binária ou sistema binário.
• É composto por dois números: 0 e 1.
• Esses números são conhecidos como bits.
• Podemos efetuar conversões entre base.
• Efetuamos operações aritméticas na base binária.

22. ANHANGUERA – 2016.2
Referências
• MONTEIRO, M. A. (org.). Introdução à Organização de Computadores. 4ª
ed. Rio de Janeiro: LTC - Livros Técnicos e Científicos, 2005, v.1.

23. Obrigado !!!
ANHANGUERA – 2016.2