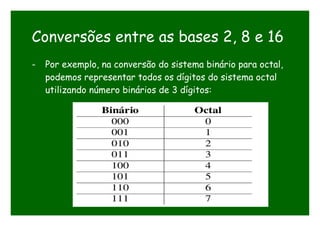
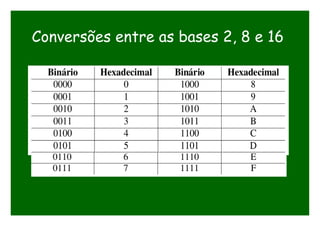
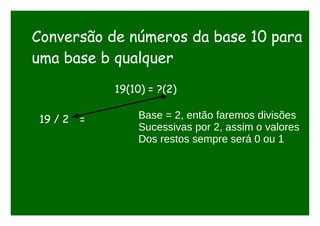
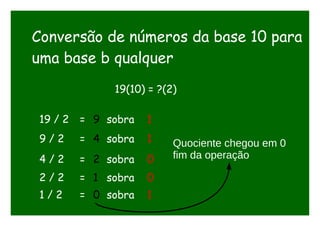
O documento discute conversões entre bases numéricas binária, octal e hexadecimal. Explica que conversões entre bases onde uma é potência da outra são mais simples, como octal (base 8) que é potência de 2. Detalha os passos para converter números entre essas bases agrupando dígitos binários em grupos de 3 para octal e 4 para hexadecimal.

1. Conversão Entre Bases
Prof: João Gonçalves Filho
Curso: Análise e Desenvolvimento de Sistemas
Disciplina: Arquitetura de Computadores

2. Conversões entre as bases 2, 8 e 16
- Uma Conversão onde uma base é potência de outra
é mais simples:
8 = 2³
16 = 2
4
- POR QUE?

3. Conversões entre as bases 2, 8 e 16
- Por exemplo, na conversão do sistema binário para octal,
podemos representar todos os dígitos do sistema octal
utilizando número binários de 3 dígitos:

4. Conversões entre as bases 2, 8 e 16
- Dessa forma, como ficaria o seguinte número binário em
Octal?
101010011(2) = ?(8)

5. Conversões entre as bases 2, 8 e 16
- Dessa forma, como ficaria o seguinte número binário em
Octal?
101010011(2) = ?(8)
- Agrupamos cada grupo de três dígitos e transformamos
em octal.

6. Conversões entre as bases 2, 8 e 16
101010011(2) =
Qual valor em octal desses três dígitos?

7. Conversões entre as bases 2, 8 e 16
101010011(2) =
Qual valor em octal desses três dígitos?
- Checar na tabela

8. Conversões entre as bases 2, 8 e 16
101010011(2) =
Qual valor em octal desses três dígitos?
- Checar na tabela
- Fazer o cálculo

9. Conversões entre as bases 2, 8 e 16
101010011(2) =
101(2) = 1x2² + 0 x 2¹ + 1 x 2
0

10. Conversões entre as bases 2, 8 e 16
101010011(2) =
101(2) = 1x2² + 0 x 2¹ + 1 x 2 = 5(8)
0
- OBS: Essa conversão funciona devido os valores de 0 a 7
em octal serem os mesmo de 0 a 7 em decimal.

11. Conversões entre as bases 2, 8 e 16
101010011(2) = 5
101(2) = 1x2² + 0 x 2¹ + 1 x 2 = 5
0

12. Conversões entre as bases 2, 8 e 16
101010011(2) = 5
010(2) = 0x2² + 1 x 2¹ + 0 x 2 = 2
0

13. Conversões entre as bases 2, 8 e 16
101010011(2) = 52
010(2) = 0x2² + 1 x 2¹ + 0 x 2 = 2
0

14. Conversões entre as bases 2, 8 e 16
101010011(2) = 52
011(2) = 0x2² + 1 x 2¹ + 1 x 2 = 3
0

15. Conversões entre as bases 2, 8 e 16
101010011(2) = 523(8)

16. Conversões entre as bases 2, 8 e 16
- Mas se não for possível formar grupo de três dígitos?
1011(2) = ?(8)

17. Conversões entre as bases 2, 8 e 16
- Mas se não for possível formar grupo de três dígitos?
1011(2) = ?(8)
- Completamos com zeros à esquerda do número!

18. Conversões entre as bases 2, 8 e 16
001011(2) = ?(8)

19. Conversões entre as bases 2, 8 e 16
001011(2) =
001(2) = 0x2² + 0 x 2¹ + 1 x 2 = 1
0

20. Conversões entre as bases 2, 8 e 16
001011(2) = 1
001(2) = 0x2² + 0 x 2¹ + 1 x 2 = 1
0

21. Conversões entre as bases 2, 8 e 16
001011(2) = 1
011(2) = 0x2² + 1 x 2¹ + 1 x 2 = 3
0

22. Conversões entre as bases 2, 8 e 16
001011(2) = 13
011(2) = 0x2² + 1 x 2¹ + 1 x 2 = 3
0

23. Conversões entre as bases 2, 8 e 16
001011(2) = 13(8)

24. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)

25. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
- Checar na tabela
- Fazer o cálculo

26. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
- Para transformar 5(8) para binário, sem olhar na tabela,
podemos fazer divisões sucessivas por 2 e pegar o resto
para formar o valor

27. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2

28. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1

29. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1
2/ 2 =

30. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1
2/ 2 = 1 sobra 0

31. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1
2/ 2 = 1 sobra 0
1/ 2 =

32. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1
2/ 2 = 1 sobra 0
1/ 2 = 0 sobra 1

33. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1
2/ 2 = 1 sobra 0
1/ 2 = 0 sobra 1
Quociente chegou em 0
indica fim da operação

34. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1
2/ 2 = 1 sobra 0
1/ 2 = 0 sobra 1

35. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = ?(2)
5/ 2 = 2 sobra 1
2/ 2 = 1 sobra 0
1/ 2 = 0 sobra 1
101(2)

36. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101

37. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101
2/ 2

38. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101
2/ 2 = 1 sobra 0

39. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101
1/ 2 =
2/ 2 = 1 sobra 0

40. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101
1/ 2 = 0 sobra 1
2/ 2 = 1 sobra 0

41. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101
1/ 2 = 0 sobra 1
2/ 2 = 1 sobra 0

42. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101
1/ 2 = 0 sobra 1
2/ 2 = 1 sobra 0
10(2)

43. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101
1/ 2 = 0 sobra 1
2/ 2 = 1 sobra 0
010(2)

44. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101010

45. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101010
3/ 2 =

46. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101010
3/ 2 = 1 sobra 1
1/ 2 =

47. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101010
3/ 2 = 1 sobra 1
1/ 2 = 0 sobra 1

48. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101010
3/ 2 = 1 sobra 1
1/ 2 = 0 sobra 1
11(2)

49. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101010
3/ 2 = 1 sobra 1
1/ 2 = 0 sobra 1
011(2)

50. Conversões entre as bases 2, 8 e 16
- No caso da conversão de octal para binário, transforma-se
1 dígito octal em 3 binários
523(8) = 101010011(2)

51. Conversões entre as bases 2, 8 e 16
- A conversão de binário para hexadecimal é feita da mesma
forma que é feita para octal, mas dessa vez agrupamos
em 4 dígitos.
10101001(2) = ?(16)
- Fique atento aos números que são reprensentados por
letras: A, B, C, D, E, F.

52. Conversões entre as bases 2, 8 e 16

53. Conversões entre as bases 2, 8 e 16
10101001(2) = ?(16)
1001(2) = 1x2³+ 0x2² + 1 x 2¹ + 0 x 2 =0

54. Conversões entre as bases 2, 8 e 16
10101001(2) = ?(16)
1001(2) = 1x2³+ 0x2² + 1 x 2¹ + 0 x 2 = 100

55. Conversões entre as bases 2, 8 e 16
10101001(2) = A

56. Conversões entre as bases 2, 8 e 16
10101001(2) = A
1001(2) = 1x2³+ 0x2² + 0 x 2¹ + 1 x 2 = 90

57. Conversões entre as bases 2, 8 e 16
10101001(2) = A9(16)

58. Conversões entre as bases 2, 8 e 16
A9(16) = ?(2)

59. Conversões entre as bases 2, 8 e 16
A9(16) = ?(2)
10/ 2 = 5 sobra 0
A = 10

60. Conversões entre as bases 2, 8 e 16
A9(16) = ?(2)
10/ 2 = 5 sobra 0
A = 10
5 / 2 = 2 sobra 1

61. Conversões entre as bases 2, 8 e 16
A9(16) = ?(2)
10/ 2 = 5 sobra 0
A = 10
5 / 2 = 2 sobra 1
2 / 2 = 1 sobra 0

62. Conversões entre as bases 2, 8 e 16
A9(16) = ?(2)
10/ 2 = 5 sobra 0
A = 10
5 / 2 = 2 sobra 1
2 / 2 = 1 sobra 0
1 / 2 = 0 sobra 1

63. Conversões entre as bases 2, 8 e 16
A9(16) = ?(2)
10/ 2 = 5 sobra 0
A = 10
5 / 2 = 2 sobra 1
2 / 2 = 1 sobra 0
1 / 2 = 0 sobra 1
1010(2)

64. Conversões entre as bases 2, 8 e 16
A9(16) = 1010
9/ 2 = 4 sobra 1

65. Conversões entre as bases 2, 8 e 16
A9(16) = 1010
9/ 2 = 4 sobra 1
4/ 2 = 2 sobra 0

66. Conversões entre as bases 2, 8 e 16
A9(16) = 1010
9/ 2 = 4 sobra 1
4/ 2 = 2 sobra 0
2/ 2 = 1 sobra 0

67. Conversões entre as bases 2, 8 e 16
A9(16) = 1010
9/ 2 = 4 sobra 1
4/ 2 = 2 sobra 0
2/ 2 = 1 sobra 0
1/ 2 = 0 sobra 1

68. Conversões entre as bases 2, 8 e 16
A9(16) = 1010
9/ 2 = 4 sobra 1
4/ 2 = 2 sobra 0
2/ 2 = 1 sobra 0
1/ 2 = 0 sobra 1

69. Conversões entre as bases 2, 8 e 16
A9(16) = 1010
9/ 2 = 4 sobra 1
4/ 2 = 2 sobra 0
2/ 2 = 1 sobra 0
1/ 2 = 0 sobra 1
1001(2)

70. Conversões entre as bases 2, 8 e 16
A9(16) = 10101001(2)

71. Conversões entre as bases 2, 8 e 16
- Para converter de hexadecimal para octal ou vice-versa.
Primeiramente podemos converter para binário e do
binário convertemos para a base desejada
A9(16) = 10101001(2)

72. Conversões entre as bases 2, 8 e 16
- Para converter de hexadecimal para octal ou vice-versa.
Primeiramente podemos converter para binário e do
binário convertemos para a base desejada
010101001(2) =251(8)
A9(16) = 10101001(2)
Coloca um '0' para poder agrupar
em grupo de 3 dígitos

73. Conversões entre as bases 2, 8 e 16
A9(16) = 251(8)

74. Conversão de números em uma base b
qualquer para a base 10
- Dado um número N de base b com n dígitos. Para
conveter para base decimal, utilizamos a
seguinte expressão:

75. Conversão de números em uma base b
qualquer para a base 10
- Para exemplificar, vamos converter as bases
anteriores para decimal.

76. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2
5

77. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2
5 4

78. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³
5 4

79. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2²
5 4

80. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹
5 4

81. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2
5 4
0

82. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) =

83. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) = 10 x 16¹

84. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) = 10 x 16¹ + 5 x 160

85. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) = 10 x 16¹ + 5 x 16 = 165(10)0

86. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) = 10 x 16¹ + 5 x 16 = 165(10)0
485(8) = 4 x 8²

87. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) = 10 x 16¹ + 5 x 16 = 165(10)0
485(8) = 4 x 8² + 8 x 8¹

88. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) = 10 x 16¹ + 5 x 16 = 165(10)0
485(8) = 4 x 8² + 8 x 8¹ + 5 x 80

89. Conversão de números em uma base b
qualquer para a base 10
101101(2) = 1 x 2 + 0 x 2 + 1 x 2³ +
1 x 2² + 0 x 2¹ + 1 x 2 = 45(10)
5 4
0
A5(16) = 10 x 16¹ + 5 x 16 = 165(10)0
485(8) = 4 x 8² + 8 x 8¹ + 5 x 8 = 325(10)0

90. Conversão de números da base 10 para
uma base b qualquer
- Nesse caso, fazemos sucessivas divisões inteiras por
b, até que o quociente da divisão chegue em 0

91. Conversão de números da base 10 para
uma base b qualquer
- Nesse caso, fazemos sucessivas divisões inteiras por
b, até que o quociente da divisão chegue em 0.
- Assim o número será formado pelos número formado
por os restos das divsões( de trás para frente).

92. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = Base = 2, então faremos divisões
Sucessivas por 2, assim o valores
Dos restos sempre será 0 ou 1

93. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1

94. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 =

95. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1

96. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 =

97. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 = 2 sobra 0

98. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 = 2 sobra 0
2 / 2 =

99. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 = 2 sobra 0
2 / 2 = 1 sobra 0

100. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 = 2 sobra 0
2 / 2 = 1 sobra 0
1 / 2

101. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 = 2 sobra 0
2 / 2 = 1 sobra 0
1 / 2 = 0 sobra 1
Quociente chegou em 0
fim da operação

102. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 = 2 sobra 0
2 / 2 = 1 sobra 0
1 / 2 = 0 sobra 1

103. Conversão de números da base 10 para
uma base b qualquer
19(10) = ?(2)
19 / 2 = 9 sobra 1
9 / 2 = 4 sobra 1
4 / 2 = 2 sobra 0
2 / 2 = 1 sobra 0
1 / 2 = 0 sobra 1
= 10011(2)

104. Conversão de números da base 10 para
uma base b qualquer
19(10) = 10011(2)

105. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)

106. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 =

107. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra 12

108. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra 12
66 / 16=

109. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra 12
66 / 16 = 4 sobra 2

110. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra 12
66 / 16 = 4 sobra 2
4 / 16 =

111. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra 12
66 / 16 = 4 sobra 2
4 / 16 = 0 sobra 4

112. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra 12 = C
66 / 16 = 4 sobra 2
4 / 16 = 0 sobra 4

113. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra C
66 / 16 = 4 sobra 2
4 / 16 = 0 sobra 4

114. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra C
66 / 16 = 4 sobra 2
4 / 16 = 0 sobra 4

115. Conversão de números da base 10 para
uma base b qualquer
1068(10) = ?(16)
1068 / 16 = 66 sobra C
66 / 16 = 4 sobra 2
4 / 16 = 0 sobra 4
= 42C(16)

116. Conversão de números da base 10 para
uma base b qualquer
1068(10) = 42C(16)

117. Bibliografia
- Introdução à Computação por Gilberto Farias
e Eduardo Santana Medeiros
- Dale, Nell; Lewis, John. Ciência da
Computação. Quarta Edição. LTC, 2011.