Transferir como PDF, PPTX
Carregado porGustavo Yoshio Maruyama
Códigos BCD, Gray e ASCII
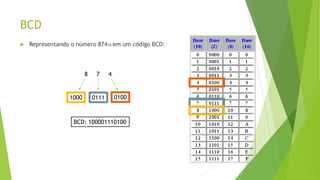
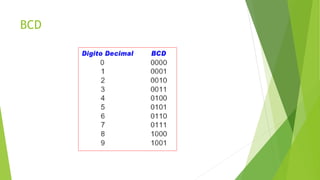
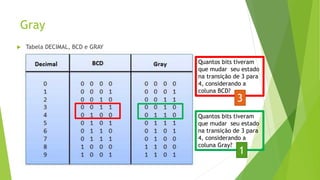
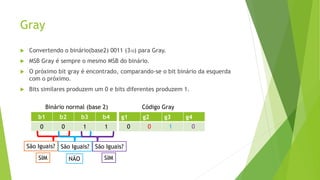
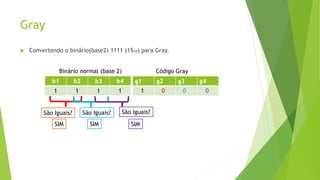
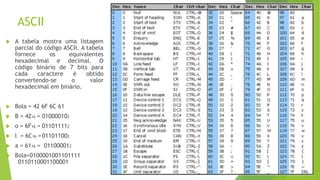
O documento descreve e compara diferentes códigos digitais, incluindo BCD, Gray e ASCII. Explica como cada código representa números ou caracteres e as vantagens de cada um, como a capacidade do código Gray de detectar erros em transições entre números.
Mais conteúdo relacionado
Semelhante a Códigos BCD, Gray e ASCII
Códigos BCD, Gray e ASCII
- 1. Códigos – BCD-GRAY- ASCII Prof. Gustavo Yoshio Maruyama
- 2. Objetivos Entender ascaracterísticas dos seguintes códigos: Código BCD Código Gray Código ASCII
- 3. Códigos Quando números,letras, ou palavras são representadas por um grupo especial de símbolos, dizemos que estão codificados. Ex.: Código Morse
- 4. Códigos Os sistemasdigitais apenas códigos que consistem em 0s e 1s. Isto se deve à natureza biestável dos circuitos eletrônicos digitais. Em um sistema digital, tradutores eletrônicos (chamados codificadores e decodificadores) são usados para converter de código a código .
- 5. BCD Vimos quequalquer decimal pode ser representado por um binário equivalente. Todos os sistemas digitais usam algum modo de numeração binária em suas operações internas; porém o mundo externo é naturalmente decimal. Isto significa que conversões entre sistemas decimal e binário são realizados frequentemente. Um número de base decimal pode ser convertidos para base binária como visto em aulas anteriores. Porém é possível representar tal número de base 10 em um equivalente em código BCD. BCD = Binary-coded-decimal (decimal codificado em binário)
- 6. BCD Representando onúmero 87410 em um código BCD: 8 7 4 010001111000 BCD: 100001110100
- 7. BCD BCD paradecimal: BCD: 1 0 0 0 0 1 1 1 0 1 0 0 478
- 8. BCD Como visto,é muito parecido com a conversão Hexadecimal x Binária. Sempre separando em grupos de 4 bits (da direita para esquerda). Porém, em código BCD NUNCA HAVERÁ a ocorrência dos seguintes códigos: • 1010 • 1011 • 1100 • 1101 • 1110 • 1111 Se qualquer um desses números de 4 bits “proibidos” aparecer alguma vez em um máquina que use o código BCD, é, geralmente uma indicação que ocorreu algum erro. BCD NÃO É CONVERSÃO HEXADECIMAL PARA BINÁRIO, VICE-VERSA.
- 9. BCD Se analisarmosmelhor perceberemos que se efetuarmos a conversão DECIMAL x BINÁRIO da forma tradicional, teremos: Bem diferente do código BCD: 874/2 = 437 resto = 0 437/2 = 218 resto = 1 218/2 = 109 resto = 0 109/2 = 54 resto = 1 54/2 = 27 resto = 0 27/2 = 13 resto = 1 13/2 = 6 resto = 1 6/2 = 3 resto = 0 3/2 = 1 resto = 1 87410 = 11011010102 874 em BCD: 100001110100 PORTANTO BCD não é: Conversão DECIMAL x BINÁRIA Conversão HEXADECIMAL x BINÁRIA (vice-versa) BCD é uma forma de CODIFICAÇÃO
- 10.
- 11. Gray Os sistemasdigitais operam em altas velocidades e reagem a variações que ocorrem nas entradas digitais. Assim como na vida, quando várias condições de entrada variam ao mesmo tempo, a situação pode ser mal interpretada e provocar reação errônea. A fim de reduzir a probabilidade de um circuito digital interpretar mal uma entrada que está mudando, desenvolveu-se o código Gray para representar uma sequência de números. A única característica distintiva do código Gray é que apenas um bit muda entre dois números sucessivos na sequência
- 12. Gray Tabela DECIMAL,BCD e GRAY Quantos bits tiveram que mudar seu estado na transição de 3 para 4, considerando a coluna BCD? Quantos bits tiveram que mudar seu estado na transição de 3 para 4, considerando a coluna Gray? 3 1
- 13. Gray Convertendo obinário(base2) 0011 (310) para Gray. MSB Gray é sempre o mesmo MSB do binário. O próximo bit gray é encontrado, comparando-se o bit binário da esquerda com o próximo. Bits similares produzem um 0 e bits diferentes produzem 1. b1 b2 b3 b4 0 0 1 1 g1 g2 g3 g4 Binário normal (base 2) Código Gray 0 São Iguais? SIM 0 São Iguais? NÃO 1 São Iguais? SIM 0
- 14. Gray Convertendo obinário(base2) 1111 (1510) para Gray. b1 b2 b3 b4 1 1 1 1 g1 g2 g3 g4 Binário normal (base 2) Código Gray 1 São Iguais? SIM 0 São Iguais? SIM 0 São Iguais? SIM 0
- 15.
- 16. ASCII Além dedados numéricos, um computador precisa ser capaz de manipular informações não numéricas. Em outras palavras um computador deve reconhecer códigos que representam letras do alfabeto, sinais de pontuação e outros caracteres especiais, assim como números. O código alfanumérico mais utilizado é o Código Padrão Americano para Troca de Informações (American Standart Code for Information Interchange – ASCII) Código de 7 bits, portanto é possível representar 128 símbolos (2^7) .
- 17. ASCII A tabelamostra uma listagem parcial do código ASCII. A tabela fornece os equivalentes hexadecimal e decimal. O código binário de 7 bits para cada caractere é obtido convertendo-se o valor hexadecimal em binário. Bola = 42 6F 6C 61 B = 4216 = 010000102 o = 6F16 = 011011112 l = 6C16 =011011002 a = 6116 = 011000012 Bola=0100001001101111 0110110001100001
- 18. UTF-8 UTF-8 (8-bitUnicode Transformation Format) é um tipo de codificação Unicode de comprimento variável criado por Ken Thompson e Rob Pike. Pode representar qualquer carácter universal padrão do Unicode, sendo também compatível com o ASCII. Por esta razão, está lentamente a ser adaptado como tipo de codificação padrão para email, páginas web, e outros locais onde os caracteres são armazenados. UTF-8 usa de um a quatro bytes (estritamente, octetos) por carácter, dependendo do símbolo Unicode que representa. É necessário apenas um byte para codificar os 128 caracteres ASCII. São necessários dois bytes para caracteres Latinos com diacríticos. São também usados dois bytes para representar caracteres dos alfabetos Grego, Cirílico, Armênio, Hebraico, Sírio e Thaana (Unicode U+0080 a U+07FF). São necessários três bytes para o resto do Plano Multilingual Básico (que contém praticamente todos os caracteres comuns utilizados). Existem ainda outros caracteres que necessitam de quatro bytes. http://dev.networkerror.org/utf8/
- 19. Exercícios 1. Transforme osseguintes números decimais para código BCD: a) 158 b) 95 c) 1024 2. Transforme os seguintes BCDs para Decimal quando possível: a) 10000010 b) 001010010101 c) 00011110 3. Transforme os seguintes números Binários para código Gray: a) 100010 b) 01001101 c) 0011110 4. Considerando a Tabela ASCII, de o número Binário da palavra “Casa”