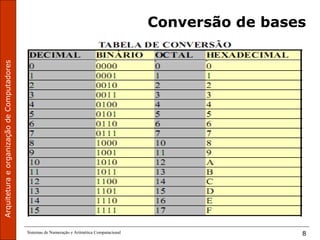
- Discute sistemas de numeração posicionais e não-posicionais, com foco nos sistemas binário, octal, decimal e hexadecimal usados em computadores - Explica conversões entre bases numéricas, incluindo métodos para converter decimal para outras bases e vice-versa

1. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 1
Arquitetura e Organização deArquitetura e Organização de
ComputadoresComputadores
Sistemas de Numeração
e
Aritmética Computacional

2. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 2
Sumário
• Sistemas de Numeração
• Conversão entre bases

3. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 3
Sistemas de numeração
• Sistemas de numeração são formas de representação de
valores.
• Existem os sistemas não-posicionais e os posicionais.
• Nos não-posicionais o símbolo não depende da posição.
Por exemplo, os numerais romanos: o símbolo X vale 10
em qualquer posição que estiver no número, seja IX ou
LXV.
• Já nos posicionais, o valor do símbolo muda com a
posição. Por exemplo: o símbolo 6 dentro do número 625
significa o valor 600, mas no número 461 significa 60.
• Diariamente trabalhamos com o sistema posicional
decimal, assim chamado por ter dez símbolos:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
• Como tem dez símbolos, dizemos também que possui
base 10.

4. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 4
Sistemas de numeração
• Como sabemos, o computador funciona em binário, ou
seja, representações de número somente com os símbolos
0 e 1.
• Este é um sistema de numeração com base 2 ou binário.
• Na eletrônica ainda é comum trabalhar-se com o sistema
octal, que possui base 8, cujos símbolos são: 0, 1, 2, 3,
4, 5, 6, 7.
• Para o endereçamento da memória do computador é
utilizado o sistema de numeração hexadecimal, de base
16, formado pelos símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A,
B, C, D, E, F.
• São estes quatro sistemas de numeração que serão o
fundamento do estudo da computação, sendo necessários
para compreensão da organização de sua arquitetura.
• Para compreendermos melhor a relação entre eles,
devemos estudar a conversão de uma base para outra.

5. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 5
Conversão de bases
Conversão de decimal para binário, octal e
hexadecimal
• Para conversão de decimal para binário, temos o exemplo:
• (174,25)10: 174 / 2 = 87 resto 0
• 87 / 2 = 43 resto 1
• 43 / 2 = 21 resto 1
• 21 / 2 = 10 resto 1
• 10 / 2 = 5 resto 0
• 5 / 2 = 2 resto 1
• 2 / 2 = 1 resto 0
• último quociente: 1 ==> parte inteira: 10101110
• 0,25 x 2 = 0,50 inteiro 0
• 0,50 x 2 = 1,0 inteiro 1 ==> parte fracionária: 01
(174,25)10 = (10101110,01)2

6. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 6
Conversão de bases
Conversão de decimal para binário, octal e
hexadecimal
• De decimal para octal:
• (749,97)10: 749 / 8 = 93 resto 5
• 93 / 8 = 11 resto 5
• 11 / 8 = 1 resto 3
• último quociente: 1 ==> parte inteira: 1355
• 0,97 x 8 = 7,76 inteiro 7
• 0,76 x 8 = 6,08 inteiro 6
• 0,08 x 8 = 0,64 inteiro 0 ==> parte fracionária: 760
(749,97)10 = (1355,760)8

7. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 7
Conversão de bases
Conversão de decimal para binário, octal e
hexadecimal
• E de decimal para hexadecimal:
• (155,742)10: 155 / 16 = 9 resto 11 (B)
• último quociente: 9 ==> parte inteira: 9B
• 0,742 x 16 = 11,872 inteiro 11 (B)
• 0,872 x 16 = 13,952 inteiro 13 (D)
• 0,952 x 16 = 15,232 inteiro 15 (F) ==> parte fracionária:
• BDF (155,742)10 = (9B,BDF)16

8. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 8
Conversão de bases

9. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 9
Conversão de bases
De binário, octal, e hexadecimal para decimal
• Segue-se a regra simples:
• Ou seja, eleva-se a base a converter à potência cujo valor
é sua posição no número e multiplica-se pelo símbolo.
• Assim, de binário (base 2) para decimal (base 10),
podemos fazer, por exemplo:
•
• Ex1:
•
• Ex2:

10. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 10
Conversão de bases
De binário, octal, e hexadecimal para decimal
• E de octal (base 8) para decimal:
• Finalmente, de hexadecimal (base 16) para decimal:

11. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 11
Conversão de bases
Conversão de decimal para binário, octal e hexadecimal
• Para converter números da base 10 para outras bases, segue-
se a seguinte regra:
• parte inteira: divide-se o número a ser convertido pela base
desejada; toma-se o quociente resultante e divide-se
novamente pela base até que o quociente seja zero; os restos
das divisões formam a parte inteira do número convertido; o
primeiro resto representa o último dígito da parte inteira do
número; o último quociente representa o primeiro dígito da
parte inteira;
• parte fracionária: multiplica-se a parte fracionária do número
a ser convertido pela base desejada; toma-se a parte
fracionária do número resultante e repete-se a operação; a
parte inteira dos produtos obtidos representam a parte
fracionária do número procurado.

12. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 12
Conversão de bases
Conversão de binário para octal
• Basta converter cada três símbolos binários em
um octal, partindo-se da vírgula. Caso faltem
símbolos para completar três, completa-se com
zeros.
• Exemplo:
(010 101,110 1)2 = (25,64)8

13. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 13
Conversão de bases
Conversão de octal para binário
• O oposto do método anterior: pega-se cada valor
e converte-se pela tabela em três símbolos
binários.
• Exemplo:
(356,71)8 = (11 101 110,111 001)2

14. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 14
Conversão de bases
Conversão de binário para hexadecimal
• Semelhante a conversão de octal, apenas
pegando cada quatro símbolos binários para um
hexadecimal, convertidos a partir da tabela.
• Exemplo:
(1101 1010 0100,1010 11)2 = (DA4,AC)16

15. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 15
Conversão de bases
Conversão de hexadecimal para binário
• Oposto do método anterior.
• Exemplo:
(CAFE,01)16 = (1100 1010 1111 1110,0000 0001)2

16. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 16

17. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 17