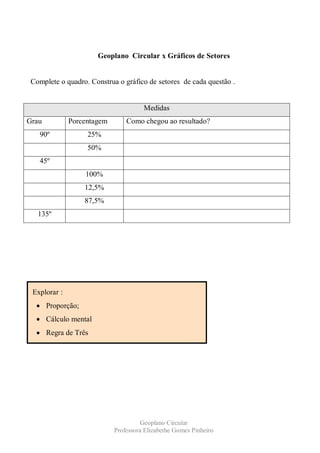
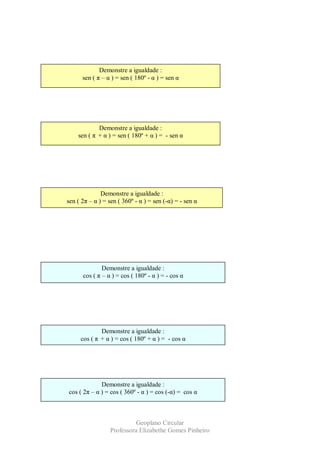
Este documento fornece um roteiro de atividades para explorar frações, gráficos de setores, ângulos, circunferências e trigonometria no contexto de um geoplano circular. Inclui demonstrações de propriedades e exercícios para praticar operações com frações, cálculo de porcentagens, construção e classificação de ângulos, e conceitos básicos de trigonometria.

1. ROTEIRO DE ATIVIDADES PARA O GEOPLANO CIRCULAR
Elizabethe Gomes Pinheiro
bethematica@hotmail.com
Geoplano Circular x Frações
Demonstre que :
a) 1/3 + 1/4 = 7/12
b) 2/3 – 1/4 = 1/3 + 1/12
c) 1/6 + 3/8 = 13/24
d) 3/4 - 1/8 = 1/2 + 1/8
e) 1/2 de 1/4 = 1/8
f) 1/4 de 8/12 = 1/6
Explorar :
Frações equivalentes;
Operações com frações;
Demonstração de mecanismos de cálculos.
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

2. Geoplano Circular x Gráficos de Setores
Complete o quadro. Construa o gráfico de setores de cada questão .
Medidas
Grau Porcentagem Como chegou ao resultado?
90º 25%
50%
45º
100%
12,5%
87,5%
135º
Explorar :
Proporção;
Cálculo mental
Regra de Três
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

3. Geoplano Circular x Ângulos
1) Construa os seguintes ângulos com as cores indicadas e classifique-os em agudo,
obtuso ou raso.
30º 90º 45º
120º 270º Crie você
2) Calcule a medida de um Ângulo que é igual ao triplo de seu suplemento.
3) A medida de um ângulo é igual à medida de seu complemento. Quem é esse ângulo
?
4) Demonstre que :
a) 2/3 de 45º é igual a 30º .
b) 1/4 de 60º é igual a 15º .
c) 3/4 de 120º é um ângulo reto.
d) 80% de 225º é igual a 180º .
e) Crie você
5) Construa os ângulos abaixo e trace a bissetriz de cada um deles. .
Obs.: construa o ângulo com elástico verde e a bissetriz com elástico de outra cor.
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

4. a) 120º b) 270º
c) 90º d) 30º
e) 330º f) Crie você
6) Demonstre que:
I – Dois ângulos opostos pelo vértice são congruentes.
II - Dois ângulos complementares são sempre agudos.
III – Duas retas perpendiculares sempre formam 4 ângulos retos .
Explorar :
Ângulos congruentes. Consecutivos e adjacentes;
Ângulos O.P.V. , Complementares e Suplementares;
Bissetriz de um ângulo
Retas paralelas, concorrentes e perpendiculares.
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

5. Geoplano Circular x Circunferência
Demonstre que :
I – Em qualquer circunferência o diâmetro é o dobro da medida do raio.
II – Toda reta tangente a uma circunferência é perpendicular ao raio no ponto de
tangência.
III – A medida de um ângulo inscrito é igual a metade da medida do arco correspondente..
Explorar :
Raio, Corda e Diâmetro ;
Retas secantes, tangentes e externas;
Ângulo Central e ângulo inscrito.
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

6. Geoplano Circular x Polígonos Regulares
1) Numa circunferência, inscreve-se um hexágono regular. Quanto mede, em graus, o
ângulo formado por dois lados consecutivos do hexágono ?
2) Demonstre as fórmulas dos polígonos regulares.
Lado apótema
Quadrado l = r √2 a = r√2 / 2
Triângulo l = r √3 a=r/2
equilátero
Hexágono regular l=r a = r √3 / 2
3) Qual é o polígono cujo nº de diagonais é igual ao nº de lados ?
Explorar
Diagonais de um polígono;
Soma dos ângulos internos;
Construção de polígonos regulares
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

7. Geoplano Circular x Trigonometria
1) Obtenha o menor ângulo formado pelos ponteiros de um relógio às
9h 30min.
2) Localize a menor determinação positiva dos seguintes ângulos:
a) 750º = cor branca
b) 825º = cor amarela
c) 3030º = cor verde
d) 1530º = cor lilás
3) Circunferência Trigonométrica é uma circunferência orientada, de
raio unitário ( r = 1 ) sobre a qual um ponto O é a origem de medida de
todos os arcos nela contados.
Localize na circunferência trigonométrica( no geoplano circular):
Os eixos do plano cartesiano
Os quadrantes ( sentido anti-horário ) .
Determine o intervalo de cada quadrante.
1º quadrante = cor lilás
2º quadrante = cor branca
3º quadrante = cor verde
4º quadrante = cor amarela
4) O Seno de um ângulo é a ordenada do ponto-extremidade do arco. Os
sinais do seno dos ângulos do 1º e 2º quadrantes são positivos e os do 3º e
4º quadrantes , negativos.
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

8. O cosseno de um ângulo é a abscissa do ponto-extremidade do arco. Os
sinais do cosseno dos ângulos do 1º e 4º quadrantes são positivos e os do 2º
e 3º quadrantes , negativos.
Observe no geoplano circular e determine os sinais de :
a) sen 30º e) cos 300º
b) sen105º f) cos 105º
c) sen 60º g) cos 60º
d) sen 90º
5 )Represente na circunferência trigonométrica as extremidades dos
arcos:
a) 45º , 135º , 225º e 315º ( cor lilás )
b) 30º , 150º , 210 º e 330º ( cor branca )
c) 60º , 120º , 240º e 300º ( cor verde )
Observe os arcos que foram representados.
Agora determine o simétricos dos ângulos notáveis:
30º ( cor verde )
45º ( cor lilás )
60º ( cor branca).
6) Comprove que :
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

9. a) cos 60º é igual a 0,5
b) sen 60º é maior que 0,5
c) cos 30º é igual ao seno de seu complemento
d) sen 30º é igual ao cosseno de seu complemento
e) sen 90º é igual a 1
f) cos 90º é igual a zero
g) seno e cosseno de 45º são iguais
h) tangente de 45º é igual a 1
7) Complete as tabelas com os sinais do seno e do cosseno:
1º quadrante 2º quadrante 3º quadrante 4º quadrante
sen x
cos x
8) Valores notáveis do seno e cosseno:
rad 0 π/2 π 3π/2 2π
Grau 0º 90º 180º 270º 360º
sen x
cos x
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

10. 9) Complete com os simétricos dos ângulos notáveis
30º
45º
60º
π/6
π/4
π/3
10) Obtenha os valores de seno e cosseno dos seguintes ângulos:
a) sen 120º =_____ cos 120º = _____
b) sen 330°= _____ cos 330º = _____
c) sen 135º = _____ cos 135º = _____
d) sen 225º = _____ cos 225º = _____
e) sen 210º = _____ cos 210º =_____
f) sen 780º = ______ cos 780º = _____
g) sen 660º = ______ cos 660º = _____
11) Simplifique :
sen ( π + α ) . sen (π – α)
sen ( - α )
12) Simplifique :
3sen 0º + 5cos 180º - 7sen 270º
sen² 90º + cos² 180º
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

11. 13) Resolva no intervalo 0 ≤ x < 2π
a) sen x = -1
b) sen x = - ½
c) cos x = - ½
d) cos² x = ½
14) Mostre que sen² x + cos ² x = 1
15) Obtenha o valor da expressão : sen 3x + cos 5x , para x = 30º
sen 4x
Geoplano Circular
Professora Elizabethe Gomes Pinheiro

12. Demonstre a igualdade :
sen ( π – α ) = sen ( 180º - α ) = sen α
Demonstre a igualdade :
sen ( π + α ) = sen ( 180º + α ) = - sen α
Demonstre a igualdade :
sen ( 2π – α ) = sen ( 360º - α ) = sen (-α) = - sen α
Demonstre a igualdade :
cos ( π – α ) = cos ( 180º - α ) = - cos α
Demonstre a igualdade :
cos ( π + α ) = cos ( 180º + α ) = - cos α
Demonstre a igualdade :
cos ( 2π – α ) = cos ( 360º - α ) = cos (-α) = cos α
Geoplano Circular
Professora Elizabethe Gomes Pinheiro