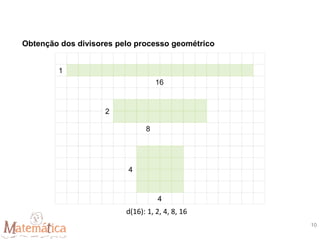
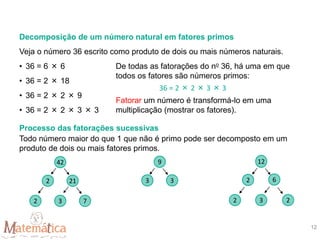
1) O documento discute conceitos de divisibilidade e decomposição de números em fatores primos. 2) É explicado como 108 é divisível por 6 mas não por 5, e como determinar se um número é divisível por 2, 3, 4, 6, 9 ou 10. 3) São mostrados métodos para encontrar todos os divisores e o máximo divisor comum (mdc) de números.

1. Divisibilidade

2. MATEMÁTICA | SADY
Divisibilidade

3. 108 alunos estão inscritos em uma
gincana. Eles serão divididos em equipes
de 6 pessoas.
Como a divisão é exata, afirmamos:
• 108 é divisível por 6
• 108 é múltiplo de 6
• 6 é divisor de 108
1 0 8 6
− 6 1 8
4 8
− 4 8
0
Divisibilidade
SÉRGIO
DOTTA
JR.
/
ARQUIVO
DA
EDITORA
3

4. Se a gincana fosse dividida em equipes
de 5 pessoas, então:
Como 108 : 5 não é divisão exata,
dizemos:
• 108 não é divisível por 5
• 108 não é múltiplo de 5
• 5 não é divisor de 108
1 0 8 5
− 1 0 2 1
0 8
− 0 5
3
Divisibilidade
SÉRGIO
DOTTA
JR.
/
ARQUIVO
DA
EDITORA
4

5. Uma papelaria vai vender 3180 cadernos que estão no estoque. O gerente
pretende fazer pacotes com a mesma quantidade de cadernos sem que
sobrem cadernos.
• 2 cadernos no pacote
Um número natural é divisível por
2 quando ele é número par.
• 3 cadernos no pacote
Um número natural é divisível por 3 quando
a soma de seus algarismos é divisível por 3.
3 1 8 0
− 2 1 5
1 1
− 1 0
1
2
8
− 1 8
0 0
9 0
3 1 8 0
− 3 1 0
0 1
− 0 0
1
3
8
− 1 8
0 0
6 0
− 0
0
5

6. • 5 cadernos no pacote
Um número natural é divisível por
5 quando termina em 0 ou 5.
• 4 cadernos no pacote
Um número natural é divisível por
4 quando o número formado pelos
seus dois algarismos da direita é
divisível por 4.
3180: é divisível por 4, porque
80 é divisível por 4.
3 1 8 0
− 2 8 7 9
3 8
− 3 6
2
4
0
− 2 0
0
5
3 1 8 0
− 3 0 6 3
1 8
− 1 5
3
5
0
− 3 0
0
6
6

7. Divisibilidade por 6
Conhecidos os critérios de divisibilidade por 2 e por 3, enunciamos:
Um número natural é divisível por 6 quando
é divisível por 2 e por 3 ao mesmo tempo.
Exemplo:
246 é divisível por 6, pois é divisível por 2 (é par)
e é divisível por 3 (2 + 4 + 6 = 12).
7

8. Divisibilidade por 9
Um número natural é divisível
por 9 quando a soma de seus
algarismos é divisível por 9.
Exemplos:
• 37 512 é divisível por 9, porque
3 + 7 + 5 + 1 + 2 = 18, e 18 é
divisível por 9.
• 984 não é divisível por 9, porque
9 + 8 + 4 = 21, e 21 não é
divisível por 9.
Divisibilidade por 10
Um número natural é
divisível por 10 quando
termina em zero (0).
Exemplos:
• 4 240 é divisível por 10, pois
termina em zero.
• 90 405 não é divisível por 10,
pois não termina em zero.
8

9. Dona Olinda fez 12 pães e pretende distribuí-los em caixas nas seguintes
condições: todas as caixas devem conter a mesma quantidade de pães e não
pode sobrar nenhum pão fora delas.
1 caixa 2 caixas 3 caixas
4 caixas 6 caixas 12 caixas
Podemos indicar os divisores de 12 assim: d(12): 1, 2, 3, 4, 6, 12
Divisores de um número natural
FOTOS:
FABIO
YOSHIHITO
MATSURA
/
ARTES:
CASA
DE
TIPOS
/
ARQUIVO
DA
EDITORA
9

10. Obtenção dos divisores pelo processo geométrico
d(16): 1, 2, 4, 8, 16
10

11. Número primo é todo número natural maior do que 1 que tem
exatamente dois divisores distintos: o 1 e ele mesmo.
Exemplos:
• 3 é um número primo, pois é maior do que 1 e só tem 1 e 3 como divisores
• 7 é um número primo, pois é maior do que 1 e só tem 1 e 7 como divisores
• 11 é um número primo, pois é maior do que 1 e só tem 1 e 11 como divisores
Crivo de Eratóstenes
1o) Construa um quadro com os números naturais.
2o) Risque os múltiplos de 2 maiores do que ele.
3o) Risque os múltiplos de 3 maiores do que ele.
4o) Risque os múltiplos de 5 e os múltiplos de 7
maiores do que eles.
5o) O maior número primo a ser checado corresponde à raiz
quadrada do valor-limite, arredondado para baixo.
Obs.: quantos números primos
há entre 0 e 100? (100 é
chamado de valor-limite)
Números primos até 100
2 3 5 7 11
13 17 19 23 29
31 37 41 43 47
53 59 61 67 71
73 79 83 89 97
Número primo
11

12. Decomposição de um número natural em fatores primos
Fatorar um número é transformá-lo em uma
multiplicação (mostrar os fatores).
Veja o número 36 escrito como produto de dois ou mais números naturais.
• 36 = 6 × 6
• 36 = 2 × 18
• 36 = 2 × 2 × 9
• 36 = 2 × 2 × 3 × 3
De todas as fatorações do no 36, há uma em que
todos os fatores são números primos:
Processo das fatorações sucessivas
Todo número maior do que 1 que não é primo pode ser decomposto em um
produto de dois ou mais fatores primos.
36 = 2 × 2 × 3 × 3
42
2 21
2 3 7
9
3 3
12
2 6
2 3 2
12

13. Processo das divisões sucessivas
• Fazemos a divisão exata de 63 pelo menor número
primo possível, que é o 3. Veja onde colocamos o
quociente 21.
• Fazemos a divisão exata de 21 pelo menor número
primo possível, que é o 3. O quociente é 7.
• Como 7 é primo, fazemos a divisão exata por ele mesmo.
• O quociente 1 indica o final do processo.
Veja um exemplo com o no 63.
63
21
7
1
3
3
7
13

14. Determinação de todos os divisores de um número
48
24
12
6
3
1
2
2
2
2
3
1
2 (2 × 1)
4 (2 × 2)
8 (2 × 4)
16 (2 × 8)
3 – 6 – 12 – 24 – 48
(3 × 1) (3 × 2) (3 ×4) (3 ×8) (3 ×16)
Veja um exemplo com o no 48.
14

15. Máximo divisor comum (mdc)
15
O máximo divisor comum (mdc) de dois ou mais números naturais é o maior
dos divisores comuns.
Exemplo:
Um garoto tem 12 selos e 30 figurinhas repetidos e quer reparti-los
igualmente entre um grupo de amigos de modo que não sobrem selos nem
figurinhas. Qual é o número máximo de amigos que o grupo pode ter para
que isso seja possível?
• 12 selos podem ser distribuídos por:
• 30 figurinhas podem ser distribuídas por:
Então, os selos e figurinhas
podem ser distribuídos ao
mesmo tempo entre:
1, 2, 3, 4, 6 ou 12 amigos
divisores de 12
1, 2, 3, 5, 6,10,15 ou 30 amigos
divisores de 30
1, 2, 3 ou 6 amigos
divisores comuns de 12 e 30

16. 120, 252 2
Processo prático para determinação do mdc
mdc(120, 252)
60, 126 2
30, 63 2
15, 63 3
5, 21 3
5, 7 5
1, 7 7
1, 1
fator comum
fator comum
só divide o 30
só divide o 21
só divide o 5
só divide o 7
fator comum
mdc(120, 252) = 2 . 2 . 3 = 12
mdc(165, 90)
165, 90 2
165, 45 3
55, 15 3
55, 5 5
11, 1 11
1, 1
3 . 5 = 15
mdc (165, 90) = 15
16

17. Mínimo múltiplo comum (mmc)
17
O mínimo múltiplo comum (mmc) de dois ou mais números naturais é o menor
número, exceto zero, que é múltiplo desses números.
Exemplo:
O médico de Sabrina receitou-lhe um comprimido de 6 em 6 horas e uma
colher de xarope de 4 em 4 horas. Sua mãe deu-lhe um comprimido e uma
colher de xarope à zero hora (meia-noite). Qual é o primeiro horário em que
Sabrina voltará a tomar comprimido e xarope ao mesmo tempo?
mmc(6,4) = 12
0, 4, 8, 12, 16, 20, 24
• horários para tomar xarope: múltiplos de 4, até 24
0, 6, 12, 18, 24
• horários para tomar o comprimido: múltiplos de 6, até 24
• horários que coincidem os remédios: 0, 12, 24 múltiplos comuns de 6 e 4, até 24
• primeiro horário após zero hora 12, que é múltiplo comum de 6 e 4.

18. Processo prático para a determinação do mmc
mmc(14, 35)
14, 35 2
7, 35 5
7, 7 7
1, 1 70 2 . 5 . 7
mmc(14, 35) =70
mmc(8, 10, 14)
8, 10, 14 2
4, 5, 7 2
2, 5, 7 2
1, 5, 7 5
1, 1, 7 7
1, 1, 1 280 2 . 2 . 2 . 5 . 7
mmc(8, 10, 14) = 280
18