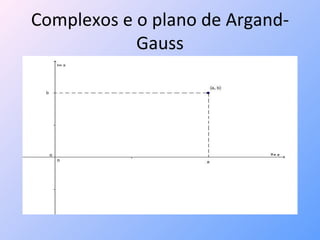
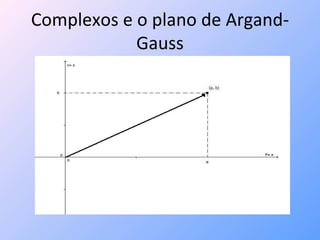
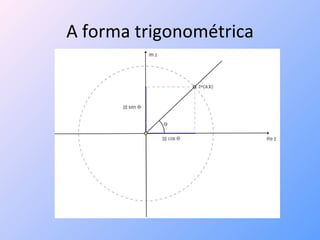
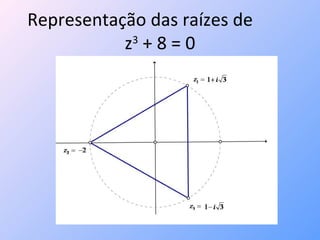
O documento explora a história dos números complexos, destacando sua origem associada à resolução de equações cúbicas no século XVI e apresentando a abordagem geométrica por Wessel, que correlaciona números complexos com o plano de Argand-Gauss. Monta-se uma estrutura matemática explicando a representação e operações com números complexos, incluindo a forma trigonométrica e suas aplicações em resolver equações binomiais, que resultam em polígonos regulares. O texto conclui que as raízes de equações binomiais representam vértices de polígonos regulares em um círculo no plano complexo.

1. Números Complexos Abordagem Geométrica: os polígonos regulares

2. Quando tudo começou... Ao final do Ensino Fundamental aprendemos que as equações do 2º grau que possuem o discriminante delta (∆) negativo não têm solução, porque não existe raiz quadrada de número negativo. Na verdade, essa informação não é totalmente verídica, haja vista que essas equações não possuem raízes reais . Essa situação gerou uma falsa impressão de que os números complexos surgiram para resolver equações do segundo grau ao considerarmos que i 2 =-1. Porém, historicamente, não foi assim que aconteceu.

3. Tudo começou no século XVI A partir de 1539 vários matemáticos apresentaram formas de resolução de equações do 3º grau. Nessa época, Cardano publicou a fórmula para resolução de equações do tipo x 3 +px=q que é: O problema surgiu quando foi tentada a resolução da equação x 3 =4+ 15x e chegou-se aos fatores e . Quem resolveu o impasse foi Bombelli, em 1572, supondo que é um número e resolvendo os termos: e para, enfim, resolver a equação:

4. E a história continua... Foram as resoluções das equações cúbicas que motivaram o estudo dos complexos e vários matemáticos ao longo dos anos tem se empenhado no desenvolvimento dos referidos números. Devido a isso, considera-se que são vários os criadores da teoria dos complexos. Então, nos ateremos apenas à parte que aborda o seu estudo geométrico. Nesse contexto, Wessel (um matemático Suíço – 1806) foi o primeiro a representar geometricamente os números complexos estabelecendo uma correspondência bijetiva entre estes e os pontos do plano, dando origem à abordagem geométrica utilizada atualmente.

5. Complexos e o plano de Argand-Gauss O conjunto dos complexos pode ser representado num sistema ortogonal de eixos semelhante ao plano cartesiano chamado de plano complexo ou plano de Argand-Gauss. Os eixos horizontal e vertical serão chamados, respectivamente, de eixo real e eixo imaginário. Nessa representação, o Conjunto dos números complexos pode ser definido por C={(a,b)/a,b ∈ R}. Então, o número complexo z=(a,b) pode ser representado como par ordenado, chamado de Afixo ou como um vetor.

6. Complexos e o plano de Argand-Gauss

7. Complexos e o plano de Argand-Gauss

8. Uma outra maneira: a forma trigonométrica Quando falamos do complexo (a,b), estamos definindo-o através de suas coordenadas cartesianas ou retangulares. Existe outra forma de escrevê-lo, por meio de seu módulo (que define sua distância à origem) e do ângulo que o correspondente vetor de posição forma com o sentido positivo do eixo horizontal, que é chamado de argumento de z (Arg z). Veremos na figura a seguir que o raio do círculo é |z| e que o ângulo que a semi-reta OZ forma com o sentido positivo do eixo reta é Ѳ = Arg (z). Além disso, escreveremos (a,b) na forma trigonométrica.

9. A forma trigonométrica

10. A forma trigonométrica Verifica-se, por meio do uso de trigonometria em triângulos retângulos, na figura anterior, que a = |z|cos Ѳ e b = |z| sen Ѳ . Então, reescrevemos um complexo na forma trigonométrica como: z = |z| (cos Ѳ + sen Ѳ ). Comparando-se com a forma z=(a,b) ou z=a + bi, temos: e cos Ѳ = a/|z| e sen Ѳ = b/|z|.

11. Complexos e a Geometria Essas são formas de escrever os números complexos apresentando-os numa abordagem geométrica. Se formos realizar operações com esses números, teremos que as somas representam translações no plano – como se fossem somas de vetores – e as multiplicações são rotações seguidas de homotetias. Mas em nosso estudo, neste trabalho, vamos nos ater à relação dos complexos com os polígonos regulares, e isso está relacionado à resoluções de potencias de complexos, como veremos adiante.

12. Equações binomiais e polígonos regulares Equações binomiais são as que podem ser escritas no tipo z n + w = 0. As soluções dessa equação são chamadas de raízes n-ésimas do complexo w, pois podemos escrevê-las da forma . Antes, apresentemos a definição de uma potência de um número complexo z = |z| (cos Ѳ + sen Ѳ ). Inicialmente, é preciso definir a multiplicação, que é z w = |z||w| (cos( Ѳ + α ) + sen( Ѳ + α )), ou seja, somam-se os argumentos e multiplicam-se os módulos. Então, em z n temos que: = |z|.|z|.|z| ... |z| (cos( θ + θ + ... + θ), sen( θ + θ + ... + θ)) =|z| n .(cos n θ, sen n θ).

13. Equações binomiais e polígonos regulares Agora, como exemplo, resolveremos z 3 + 8 = 0, o que equivale a . Escrevendo z e -8 na forma trigonométrica e substituindo na equação, temos: |z| 3 .(cos 3 θ, sen 3 θ) =8 (cosπ, senπ) . |z| 3 =2 -> |z| = 2 (daqui descobrimos que todas as raízes têm módulo 2). 3 θ = π + 2kπ (expressão geral dos arcos côngruos com π).

14. Equações binomiais e polígonos regulares Fazendo k variar em z, obtemos as raízes: k 1 =0 -> k 2 =0 -> k 3 =0 -> A partir de k=2 as respostas começam a se repetir. Portanto, existem três soluções distintas, que ao serem representadas no plano complexo formam um triângulo equilátero inscrito num círculo, cujo raio é módulo das três raízes.

15. Representação das raízes de z 3 + 8 = 0

16. E se forem raízes n-ésimas? Em equações binomiais z n + w = 0 (com w≠0), sempre encontraremos n soluções que representam os n vértices de um polígono regular de n lados, inscrito no círculo com centro na origem e raio . Os argumentos dessas n raízes são da forma , onde Ѳ é o argumento de w e k= 0, 1, 2, 3, ..., n-1.

17. Um outro exemplo Vamos resolver a equação z 4 + 1 = 0. Isso equivale a resolver . Então: |z| 4 .(cos 4 θ, sen 4 θ) =1 (cosπ, senπ) . |z| 4 =1 -> |z| = 1 4 θ = π + 2kπ -> θ = π/4 + kπ/2.

18. Representação no plano da equação z 4 + 1 = 0

19. Bibliografia Silva, Ana Lucia Vaz da. Instrumentação do ensino da Aritmética e Álgebra . v.2. Fundação Cecierj, 2005. Silva, Ana Lucia Vaz da. Instrumentação do ensino da Aritmética e Álgebra . v.3. Fundação Cecierj, 2005.