1) O documento discute números complexos, apresentando suas diferentes formas algébrica e trigonométrica, assim como operações com números complexos e suas propriedades.
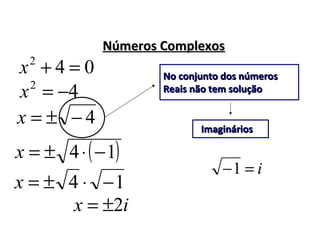
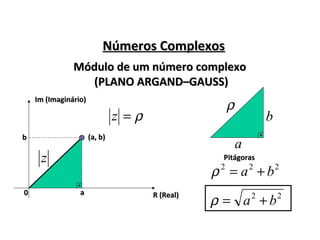
2) É introduzida a notação i=−1 e é mostrado que números complexos podem ser representados na forma a + bi, onde a é a parte real e b a parte imaginária.
3) São apresentadas as operações de adição, subtração, multiplicação e divisão com números complexos na forma algébrica, assim como suas propriedades.













































![Números ComplexosNúmeros Complexos
Operações com números complexos na forma trigonométricaOperações com números complexos na forma trigonométrica
( ) ( )[ ]21212121 cos θθθθρρ +⋅++⋅⋅=⋅ senizz
MultiplicaçãoMultiplicação
DivisãoDivisão
( ) ( )[ ]2121
2
1
2
1
cos θθθθ
ρ
ρ
−⋅+−⋅= seni
z
z
PotenciaçãoPotenciação
( ) ( )[ ]θθρ ⋅⋅+⋅⋅= nseninz nn
cos](https://image.slidesharecdn.com/numeroscomplexossemi-extensivo-180604193709/85/Numeros-complexos-semi-extensivo-50-320.jpg)
![58) (UCMG) O produto dos três números complexos:58) (UCMG) O produto dos três números complexos:
( )º40º40cos21 seniz ⋅+⋅=
é:é:
( )º135º135cos32 seniz ⋅+⋅=
( )º125º125cos13 seniz ⋅+⋅=
( ) ( )[ ]321321321321 cos θθθθθθρρρ ++⋅+++⋅⋅⋅=⋅⋅ senizzz
( ) ( )[ ]º125º135º40º125º135º40cos132321 ++⋅+++⋅⋅⋅=⋅⋅ senizzz
[ ]º300º300cos6321 senizzz ⋅+⋅=⋅⋅
[ ]º60º60cos6321 senizzz −⋅+⋅=⋅⋅
⋅−⋅=⋅⋅
2
3
2
1
6321 izzz](https://image.slidesharecdn.com/numeroscomplexossemi-extensivo-180604193709/85/Numeros-complexos-semi-extensivo-51-320.jpg)

![61) (ITA) Seja z um número complexo de módulo 1 e de61) (ITA) Seja z um número complexo de módulo 1 e de
argumentoargumento θθ , então, então é:é:n
n
z
z
1
+
*
+∈Zn
( ) ( )[ ]θθρ nisennz nn
+⋅= cos
( ) ( )θθ ⋅⋅+⋅
=
nseninzn
cos
11
∴ ( ) ( )[ ]θθ nisennz nn
+⋅= cos1
( ) ( )θθ nseninzn
⋅+= cos
( ) ( )
( ) ( )θθ
θθ
⋅⋅−⋅
⋅⋅−⋅
⋅
nsenin
nsenin
cos
cos
( ) ( )
( )[ ] ( )[ ]22
cos
cos1
θθ
θθ
⋅⋅−⋅
⋅⋅−⋅
=
nsenin
nsenin
zn](https://image.slidesharecdn.com/numeroscomplexossemi-extensivo-180604193709/85/Numeros-complexos-semi-extensivo-53-320.jpg)
![61) (ITA) Seja z um número complexo de módulo 1 e de61) (ITA) Seja z um número complexo de módulo 1 e de
argumentoargumento θθ , então, então é:é:n
n
z
z
1
+
*
+∈Zn
( ) ( )
( )[ ] ( )[ ]22
cos
cos1
θθ
θθ
⋅⋅−⋅
⋅⋅−⋅
=
nsenin
nsenin
zn
( ) ( )
( ) ( )θθ
θθ
⋅⋅−⋅
⋅⋅−⋅
=
nsenin
nsenin
zn 222
cos
cos1 ( ) ( )
( ) ( )θθ
θθ
⋅+⋅
⋅⋅−⋅
=
nsenn
nsenin
22
cos
cos
( ) ( ) =
⋅⋅−⋅
=
1
cos1 θθ nsenin
zn
( ) ( )θθ ⋅⋅−⋅ nsenincos](https://image.slidesharecdn.com/numeroscomplexossemi-extensivo-180604193709/85/Numeros-complexos-semi-extensivo-54-320.jpg)


