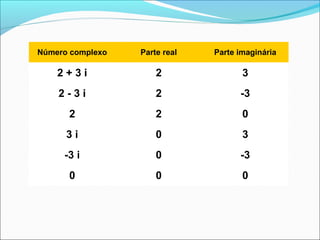
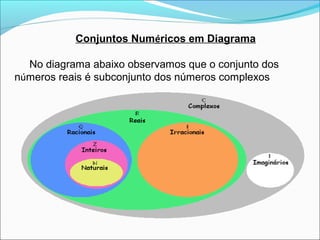
O documento aborda equações do 2º grau e a introdução dos números complexos, explicando como o discriminante determina a quantidade de raízes reais. São apresentados exemplos e operações com números complexos, incluindo adição, subtração, multiplicação e divisão. A unidade imaginária é introduzida, junto com a definição e a identificação de partes reais e imaginárias de números complexos.

2. Ao resolver uma equação do 2º grau podemos
obter três resultados, dependendo do valor do
discriminante:
Δ > 0, duas raízes reais diferentes.
Δ = 0, uma raiz real.
Δ < 0, nenhuma raiz real.

3. Quando resolvemos a equação do 2°grau
x² + 2x + 5 = 0, por exemplo,utilizando a fórmula de
Bháskara , encontramos: X = - 2 ± √-16
2
Para determinar o valor de x, é preciso calcular a
√ - 16. Porém isso é impossível em IR.

4. O surgimento dos números complexos
possibilitou obter soluções para casos em
que é necessário descobrir novos conjuntos
numéricos, onde o quadrado de um número
negativo tem como resultado um número
negativo.

5. Iremos apresentar a unidade imaginária i,
assim poderemos dizer que o quadrado de
um número é um número negativo, então
i * i = - 1, isto é, i² = - 1 .

6. i . i = - 1
Observação:
É uma outra operação que ainda carece de definição.
Não se trata de uma operação de números reais.

7. Definição de número complexo ( C )
Número complexo é todo número que pode ser
escrito na forma z = a + b i ,onde a , b ϵ IR e i é
a unidade imaginária.
O número real a é a parte real do número
complexo z e o número real b é a parte
imaginária do número complexo z, denotadas
por: a = Re(z) e b = Im(z)

8. Quais dos números abaixo são complexos?
2 + 3 i
2 - 3 i
2
3 i
-3 i
0

9. Número complexo Parte real Parte imaginária
2 + 3 i 2 3
2 - 3 i 2 -3
2 2 0
3 i 0 3
-3 i 0 -3
0 0 0

10. Conjuntos Numéricos em Diagrama
No diagrama abaixo observamos que o conjunto dos
números reais é subconjunto dos números complexos

11. A equação do 2º grau x² + 2x + 5 = 0 é
impossível de ser resolvida no conjunto dos
números Reais,mas pode ser resolvida no
conjunto dos números Complexos , da seguinte
forma:
X = - 2 ± √ - 16 = - 2 ± 4i = - 1 ± 2i
2 2
Pois,( 4i)² = 4² . i² = 16 . (-1) = -16

12. Exemplo: Equação incompleta do 2º grau
x² + 81 = 0
x² = –81
x = ± √–81
x = ± 9i
Temos, (±9i)² = (±9)² . i² = 81 .(– 1 ) = – 81

13. Exemplo: Equação completa do 2º grau
2x² - 16x + 50 = 0 ; a = 2, b = -16, c = 50
Δ = b² - 4ac
Δ = (-16)² - 4 . 2 . 50 = 256 + 400 = - 144
x’ = 4 + 3i e x’’ = 4 – 3i

14. Exercícios
1)Resolva em C, as equações abaixo:
a) x² + 4 = 0
b)x² - 4 x + 29 =0
c) x² + 9 = 0

15. 2)Identifique a parte real e a parte imaginária de
cada um dos seguintes números complexos:
a)z = 2 + 7i d)z = -10i
b)z = - 4 + 3i e)z = 5
c)z = 1 + 5 i
3

16. Solução 1:
a) x² + 4 = 0
X² = - 4
X = ± √ -4
X = ± 2i
b) x² - 4x + 29 = 0
a=1 , b = -4 ,c=29
Δ = 16 -116 = -100
X = 4 ± √ -100 = 4 ± 10i
2 2
X = 2 ± 5i

17. C) x² + 9 = 0
X² = -9
X = ± √ -9
X = ± 3i

18. 2 a)z = 2 + 7i Re(z) = 2 e Im(z)=7
b)z = -4 + 3i Re(z) = -4 e Im(z)=3
c)z = 1 + 5 i Re(z) = 1/3 e Im(z)=5/3
3
d)z = -10i Re(z) = 0 e Im(z)=-10
e)z = 5 Re(z) = 5 e Im(z)=0

19. Conjugado
Para determinarmos o conjugado de um número
complexo, basta representar o número complexo
através do oposto da parte imaginária.
_
O conjugado de z = a + bi será: z = a – bi
_
O conjugado de z = 2 +3i será: z = 2 - 3i

20. Operações com
números
complexos

21. Adição
Tratando os números complexos como binômios,
podemos realizar a sua soma reduzindo os termos
semelhantes como no exemplo abaixo:
( 8 + 4i ) + ( 2 + 5i ) =8 + 4i + 2 + 5i
= 8 + 2 + 4i + 5i = 10 + 9i
Como você pode perceber, isto é equivalente a
somarmos separadamente as suas partes reais e
imaginárias.

22. Subtração
( 7 + 8i ) – ( 2 + 6i ) = 7 + 8i – 2 – 6i
= 7 – 2 + 8i -6i = 6 + 2i
( 3 + i ) – ( 2 – 5i ) = 3 + i – 2 + 5i
= 3 – 2 + i + 5i = 1 + 6i

23. Multiplicação
Realizamos a multiplicação de números complexos
tratando-os como binômios e os multiplicando como
tal, ou seja, multiplicando cada termo do primeiro
binômio por cada termo do segundo:
( 3 + 2i ) . ( 1 + 5i ) = 3 + 15i + 2i + 10i²
= 3 +15i + 2i +10.(-1)
= 3 +15i +2i -10
= 3 -10 + 15i +2i = - 7 + 17i

24. ( 5 + 8i ) . ( 5 – 8i )= 25 -40i + 40i -64i²
=25 – 64 .(-1) = 25 +64 =89
(1 + 2i ) . ( 1 – 2i ) = 1 -2i +2i -4i² = 1 – 4.(-1) = 1+4 = 5
A multiplicação de um número imaginário pelo seu
conjugado sempre resulta em um número real e isto
pode ser utilizado para realizar a divisão de números
complexos

25. Divisão
A divisão de números complexos
é realizada multiplicando o
dividendo e o divisor pelo
conjugado do divisor.

26. Exemplo de divisão em C
4 + 2i = ( 4 + 2i ) . ( 1 – i) = 4 – 4i + 2i – 2i² =
1 + i ( 1 + i ) . ( 1 – i ) 1 – i + i – i²
= 4 – 2i -2.(-1) = 4 -2i + 2 = 2 – 2i = 1 – i
1 – ( -1 ) 1 + 1 2

27. Cálculo da potência de i
Existem apenas 4 valores para a potência de i com
expoentes inteiros:
i0 = 1 i¹ = i i² = - 1 e i³ = - i

28. A partir da potência i4 as outras
vão se repetindo de 4 em 4.
Potência Resultado Potência Resultado
i0 1 i4 1
i¹ i i5 i
i² -1 i6 -1
i³ -i i7 -i

29. in = ir
Para calcularmos por exemplo a potência i343, iremos
dividir 343 por 4, irá sobrar um resto r igual a 3, assim,
podemos concluir que i343 = i³ = - i
Vamos calcular i80 .
Quando dividimos 80 por 4 ,sobra o resto 0.
Assim: i80 = i° = 1

30. Trabalho de Pós Graduação em Matemática – UFF
Disciplina: Informática Educativa I
Tutora :Profª.: Vânia Marins
Aluna:Vania Cristina Barros de Souza

31. Referências eletrônicas
www.matematicadidática.com
www.brasilescola.com
Bibliografia:
Matemática Paiva – vol.3.Editora Moderna
Texto do professor Carlos Eduardo Mathias
Motta:O uso de software de geometria dinâmica no
ensino de um número complexo.