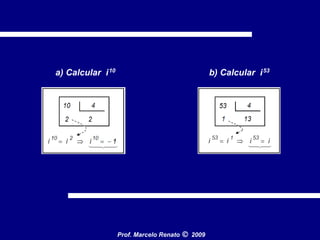
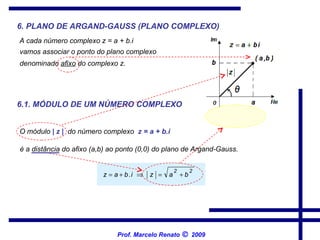
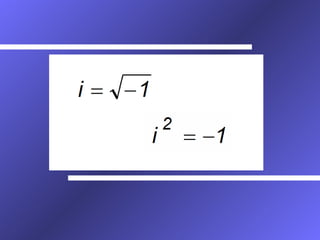Este documento apresenta uma introdução aos números complexos, começando por explicar porque surgem e definindo o conjunto dos números complexos C. Apresenta a forma algébrica de um número complexo como z = a + bi, e explica operações básicas como adição, subtração, multiplicação e divisão. Também introduz o plano complexo de Argand-Gauss e a forma trigonométrica de um número complexo.

1. NÚMEROS COMPLEXOS Prof. Marcelo Renato  2009 AULA 01 – MÓDULO 1

2. 1. INTRODUÇÃO Resolvendo a equação x 2 – 4 x + 5 = 0, utilizando a fórmula de Bháskara, Vamos calcular o delta ... Sabemos que, neste caso, NÃO EXISTEM RAÍZES REAIS ! Sabemos, também, que a equação é de grau 2 e, portanto, tem 2 raízes, certo? VAMOS APRENDER COMO LIDAR COM ESSE TIPO DE NÚMERO! ... iremos conhecer o Conjunto dos Números Complexos . Prof. Marcelo Renato  2009

3. O CONJUNTO C

4. O conjunto C representa os números Complexos; O conjunto ( C – R ) representa os números Complexos Imaginários (Complexos não-Reais) ; Todo número real é complexo, entretanto, nem todo número complexo é real; Como no conjunto dos números reais não existem números na forma foi criado o conjunto “ C ”, para abrigar tais “números”: O conjunto R representa os números Complexos Reais e é subconjunto de C ; C ( C – R ) Q N Z R Prof. Marcelo Renato  2009

6. Exemplo: Resolva a equação no campo dos números complexos. Resposta: S = { 1 – i ; 1 + i } Prof. Marcelo Renato  2009

7. 3. FORMA ALGÉBRICA DE UM NÚMERO COMPLEXO:

8. onde “ a ” é a parte real do complexo “z” e “ b ” é sua parte imaginária . 3. FORMA ALGÉBRICA DE UM NÚMERO COMPLEXO: Exemplos: z 1 = 2 + 3.i ; z 2 = – 1 + i ; z 3 = 5.i Prof. Marcelo Renato  2009

9. 4. OPERAÇÕES COM COMPLEXOS NA FORMA ALGÉBRICA

10. 4. OPERAÇÕES COM COMPLEXOS NA FORMA ALGÉBRICA 4.1. Igualdade de números complexos: 4.2. Adição / Subtração: A operação de multiplicação de dois números complexos ocorre de acordo Resolução: devemos lembrar que com a regra de multiplicação de binômios, entretanto, Prof. Marcelo Renato  2009 Exemplo: Sendo os números complexos e , calcule

11. 4.4. Conjugado: O conjugado do complexo , a e b reais, é o complexo Exemplo: Determine C , tal que Resolução: Fazendo-se z = a + b.i , teremos: Inverte-se o sinal da parte imaginária e Prof. Marcelo Renato  2009

12. DIVISÃO DE COMPLEXOS

13. 4.5. DIVISÃO DE COMPLEXOS: Exemplo: Sendo os números complexos , calcule o valor de Resolução: Para efetuarmos a divisão de dois números complexos , num procedimento semelhante à operação de racionalização de denominadores, ou seja: utilizaremos o conjugado do denominador Sendo o denominador na forma ( a + b.i ), com b  0. Prof. Marcelo Renato  2009 POR QUAL MOTIVO ?

14. Prof. Marcelo Renato  2009

15. 5. POTÊNCIAS DE “ i ”

16. Os resultados de , com o expoente “ n ” variando, Para o cálculo da potência I n , com “n” inteiro e se repetem com um período de quatro. divide-se n por 4, obtendo-se resto inteiro “ r ”. Tem-se então , 5. POTÊNCIAS DE “ i ” Prof. Marcelo Renato  2009

17. a) Calcular i 10 b) Calcular i 53 Prof. Marcelo Renato  2009

18. Observação:

19. 6. PLANO DE ARGAND-GAUSS: Parte Real Parte Imaginária Argumento Módulo Afixo Prof. Marcelo Renato  2009

20. 6. PLANO DE ARGAND-GAUSS (PLANO COMPLEXO) A cada número complexo z = a + b.i denominado afixo do complexo z. 6.1. MÓDULO DE UM NÚMERO COMPLEXO O módulo | z | do número complexo z = a + b.i é a distância do afixo (a,b) ao ponto (0,0) do plano de Argand-Gauss. vamos associar o ponto do plano complexo Prof. Marcelo Renato  2009

21. 6.2. ARGUMENTO DE UM NÚMERO COMPLEXO Denomina-se argumento do complexo, não-nulo, z = a + b.i a medida do ângulo formado pelo segmento de reta medido no sentido anti-horário, com o eixo real, Prof. Marcelo Renato  2009

22. 7. FORMA TRIGONOMÉTRICA (OU POLAR) DE UM NÚMERO COMPLEXO A forma trigonométrica de z será: Exemplo 1: Prof. Marcelo Renato  2009

23. Para passar um número complexo da forma algébrica para a forma trigonométrica devemos proceder da seguinte maneira: 1º passo: Representar o complexo no plano de Argand-Gauss 3º passo: 2º passo: Calcular o módulo e o argumento de z; Escrever z na forma Observação: Este tópico será estudado detalhadamente no módulo 02. Observação-3: Parte imaginária de z Im(z) Parte Real de z Re(z) Prof. Marcelo Renato  2009 ARCO CUJA TANGENTE VALE

24. 8. TEOREMA DAS RAÍZES COMPLEXAS NÃO REAIS, ou seja, (a + b.i) com b    0

25. 8. TEOREMA DAS RAÍZES COMPLEXAS NÃO REAIS Se um número complexo z = a + b.i, com b  0, é raiz de uma equação COM COEFICIENTES REAIS , então seu conjugado também é raiz dessa equação. Exemplo: (PUC-SP) Resolva a equação 3x 3 – 7x 2 + 8x – 2 = 0, sabendo que uma de suas raízes é 1 – i. Utilizando a relação de Girard correspondente à soma das raízes da equação: Resposta: Resolução: Como a equação possui coeficientes reais, “ (1 + i) ” também é raiz da equação. São raízes da equação: Prof. Marcelo Renato  2009

26. ESTE FOI O 1º MÓDULO DE NÚMEROS COMPLEXOS VERIFIQUE SE OS EXERCÍCIOS JÁ ESTÃO DISPONÍVEIS NO SITE http://www.marcelorenato.com.br DEPOIS DE EXERCITAR (OBJETIVAS E DISCURSIVAS), INICIE O 2º MÓDULO DE NÚMEROS COMPLEXOS ... TENHO CERTEZA QUE VOCÊ PODE MUITO MAIS !