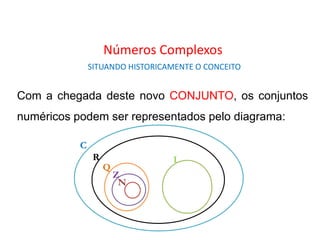
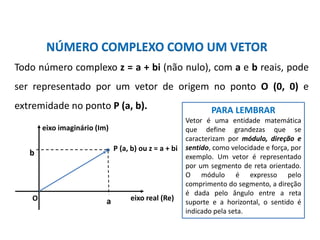
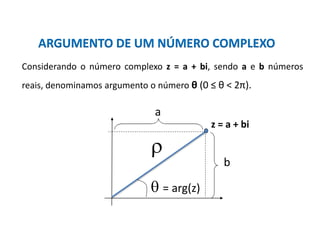
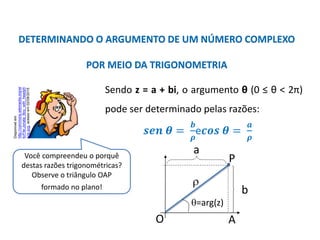
O documento descreve a história do desenvolvimento dos números complexos, começando com Nicollo Tartaglia, que formulou uma fórmula geral para resolver equações do segundo grau. Gerônimo Cardano quebrou um juramento feito a Tartaglia e publicou a fórmula de Tartaglia. Raphael Bombelli considerou a raiz quadrada de números negativos como números imaginários. Leonhard Euler usou a letra i para representar a raiz quadrada de -1. Carl Friderich Gauss ampliou o uso do símbolo i e criou a expressão "número complex