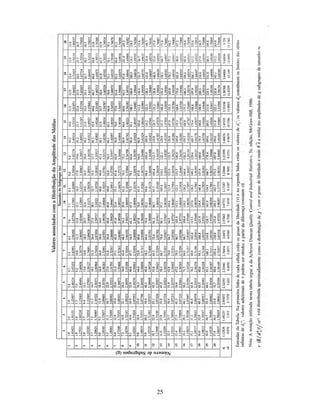
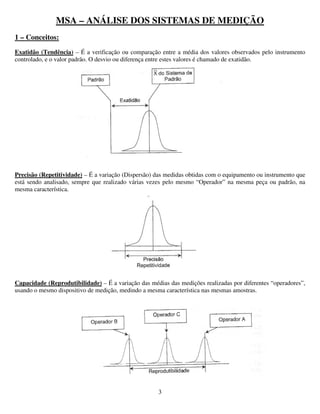
1) O documento discute conceitos e análises de sistemas de medição, incluindo tendência, linearidade, repetitividade, reprodutibilidade e estabilidade. 2) É explicado como realizar estudos para avaliar cada um desses fatores e determinar se um sistema de medição é aceitável. 3) São fornecidos detalhes sobre causas possíveis de erros em cada fator e equações para analisar os resultados dos estudos.

1. Analises dos Sistemas de Medição – MSA
3° Edição
Elaborado por: Carlos Ernesto NataliElaborado por: Carlos Ernesto NataliElaborado por: Carlos Ernesto NataliElaborado por: Carlos Ernesto Natali

2. 2
Índice
1) Conceitos ................................................................................................................... Pág. 3
2) Processos de Medição .............................................................................................. Pág. 5
3) Tendência (Bias) ..................................................................................................... Pág.7
4) Linearidade ............................................................................................................. Pág. 8
5) Estabilidade ............................................................................................................. Pág. 11
6) Repetitividade e Reprodutibilidade (R&R) .......................................................... Pág. 12
7) Estudos dos Sistemas de Medição por Atributos ................................................ Pág. 14
8) Práticas para sistema de medição complexos ou não replicáveis ......................... Pág. 15
9) Análises dos resultados ........................................................................................... Pág. 15
10) Anexos
• Tabela de distribuição t .................................................................................. Pág. 18
• Sistema de medição por atributos ................................................................ Pág. 19
• Relatório de R&R ......................................................................................... Pág. 23
• Tabela d*
2 ........................................................................................................ Pág. 25

3. 3
MSA – ANÁLISE DOS SISTEMAS DE MEDIÇÃO
1 – Conceitos:
Exatidão (Tendência) – É a verificação ou comparação entre a média dos valores observados pelo instrumento
controlado, e o valor padrão. O desvio ou diferença entre estes valores é chamado de exatidão.
Precisão (Repetitividade) – É a variação (Dispersão) das medidas obtidas com o equipamento ou instrumento que
está sendo analisado, sempre que realizado várias vezes pelo mesmo “Operador” na mesma peça ou padrão, na
mesma característica.
Capacidade (Reprodutibilidade) – É a variação das médias das medições realizadas por diferentes “operadores”,
usando o mesmo dispositivo de medição, medindo a mesma característica nas mesmas amostras.

4. 4
Estabilidade – É a diferença entre a média, de pelo menos dois conjuntos de medições realizados com um mesmo
equipamento nas mesmas amostras em ocasiões diferentes, (Período de tempo prolongado).
Mudança da tendência no decorrer do tempo.
Linearidade – Mudança da tendência ao longo do campo de operação normal. Correlação dos múltiplos e
independentes erros de tendência ao longo do campo de operação. Erro sistemático que faz parte do sistema de
medição.
GRR ou R&R do Dispositivo de Medição – Repetitividade e Reprodutibilidade do dispositivo de medição:
estimativa combinada da repetitividade e da reprodutibilidade do sistema de medição. Capabilidade do sistema de
medição: dependendo do método usado, pode incluir o efeito do tempo ou não.
Capabilidade do Sistema de Medição – Estimativa (curto prazo) da variação do sistema de medição.

5. 5
2 – Processo de Medição
Processo: É um conjunto de ações que visa transformar alguma coisa, de forma ordenada em outra diferente.
Sistemas de medição: É o conjunto de operações, procedimentos, dispositivos de medições e outros
equipamentos, software e pessoal usado para atribuir um n° à característica que está sendo medida; o processo
completo usado para obter as medidas.
Para gerenciar um processo há necessidade de saber:
• O que o processo deveria estar fazendo
• O que pode dar de errado
• O que o processo está fazendo
As especificações e os requisitos de engenharia definem aquilo que o processo deveria estar fazendo.
O propósito da Análise de Modo e efeitos da Falha Potencial do Processo (PFMEA) é definir o risco associado
com as falhas potenciais do processo e propor ação corretiva antes que tais falhas possam ocorrer. O resultado do
PFMEA é transferido para o plano de controle.
Para avaliar o processo deve-se examinar os parâmetros do processo, peças em processamento, subconjuntos
montados, ou produtos finais já feitos, com o auxílio de padrões adequados e aparatos de medição que capacitam o
observador a confirmar ou negar a premissa de que o processo está operando de maneira estável e com variação
aceitável, segundo um determinado objetivo do cliente.
Fontes de variação de um processo:
Fontes de variação de um processo de medição:

6. 6
Propriedades fundamentais que definem um bom sistema de medição:
• Discriminação e sensibilidade adequadas: Para o propósito de medir, os incrementos de medição devem ser
pequenos relativamente à variação do processo ou aos limites da especificação. A conhecida Regra dos
Dez, ou Regra do 10 a 1, expressa que a discriminação do instrumento deve dividir a tolerância (ou
variação do processo) em dez partes iguais. Esta regra prática foi proposta como ponto de partida para
seleção de um dispositivo de medição.
• O sistema de medição tem por obrigação estar sob controle estatístico. Isto significa que, sob condições
repetitivas, a variação do sistema de medição é devida somente a causas comum e não a causas especiais.
Esta situação também pode ser descrita como estabilidade estatística e é mais bem avaliada por meio de
métodos gráficos.
• Para controle do produto, a variabilidade do sistema de medição deve ser pequena quando comparada com
os limites da especificação. Avalia-se o sistema de medição contra tolerância da característica do produto.
• Para controle do processo, a variabilidade do sistema de medição deve demonstrar resolução efetiva a ser
pequena quando comparada com a variação do processo de manufatura. Avalia-se o sistema de medição
contra a variação 6-sigma do processo e/ou contra a Variação Total do estudo de análise do sistema de
medição (MSA).

7. 7
3 – Tendência (Bias)
A tendência é conhecida como “exatidão”. Não se recomenda o uso do termo “exatidão” como alternativa para
tendência, pois a palavra exatidão tem vários significados na literatura.
A tendência é a diferença entre o valor verdadeiro (valor de referência) e a média das medições observadas para
uma característica. A tendência é também a medida do erro sistemático de um sistema de medição.
As causa possíveis para uma tendência excessiva são:
• O instrumento necessita calibração
• Desgaste do instrumento, equipamento ou dispositivo de fixação
• Padrão desgastado ou danificado, erro do padrão
• Calibração inapropriada ou uso anapropriado do padrão
• Instrumento de baixa qualidade, quanto ao projeto ou a conformidade de manufatura
• Erro de Linearidade
• Dispositivo de medição diferente – ajuste, carga, aperto/fixação, técnica de operação
• Medição de característica errada
• Deformação/distorção (da peça ou do dispositivo de medição)
• Ambiente – temperatura, umidade, vibração, limpeza
• Violação de alguma premissa – erro na aplicação de uma constante
• Aplicação – tamanho da peça, posição, habilidade do operador, fadiga, erro de observação (legibilidade,
paralaxe)
O procedimento de medição empregado no processo de calibração deve ser tão idêntico quanto possível ao
procedimento de medição usado na operação normal.
Realização do Estudo de Tendência
1) Obter uma amostra e estabelecer seu valor de referência contra um padrão rastreável. Caso não haja
disponibilidade de um padrão, selecionar uma peça de produção que se situa no meio do intervalo das
medições feita na produção denominando-a de peça-padrão para efeito da análise de tendência. Medir esta
peça n ≥ 10 vezes e calcular a média dessas n leituras. Usar a média como “valor de referência”.
2) Com um avaliador, medir a peça-padrão n ≥ 10 vezes de maneira convencional.
Tendência

8. 8
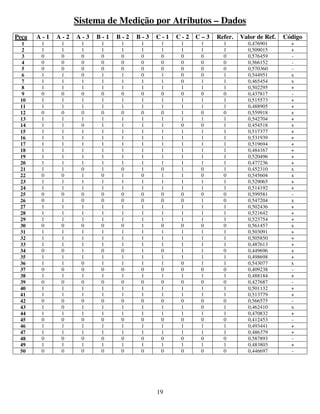
3) Com os dados obtidos, construir um histograma marcando em sua escala horizontal o valor de referência.
Analisar o histograma para determinar se estão presentes quaisquer causas especiais ou anomalias.
4) Calcular a média das n leituras.
5) Calcular o desvio padrão da repetitividade (veja também a seguir, Estudo do Dispositivo de Medição,
Método da Amplitude):
onde d*
2 é obtido na tabela
com g = 1 m = n
6) Determinar o valor estatístico t para a tendência:
7) A tendência é aceitável no nível α se o valor zero se situar dentro dos limites de confiança 1 - α, em torno
da tendência:
onde v é obtido na tabela,
com g = 1, m = n, e
tv,1-α/2 é obtido por meio das tabelas t padrão.
4 - Linearidade
a diferença da tendência ao longo do intervalo de operação esperado (medição) no equipamento é chamada de
linearidade. A linearidade pode ser imaginada como a variação da tendência com respeito ao tamanho (medido).
As causas possíveis do erro de linearidade são:
• Instrumento necessita calibração, reduzir o intervalo de tempo entre calibrações
• Desgaste do instrumento, equipamento, ou dispositivo de fixação
__
X =
n
∑=
n
i
xi
1
σσσσrepetitividade =
max (xi) – min (xi)
d*
2
σσσσb
=
σσσσr
√n
t =
tendência
σσσσb
Tendência – [σσσσb(tv,1-α/2)] Tendência + [σσσσb(tv,1-α/2)]≤ zero ≤

9. 9
• Manutenção precária – ar, energia, hidráulica, filtros, corrosão, ferrugem, limpeza
• Padrão(ões)-mestre desgastado(s) ou danificado(s), erro do(s) padrão(ões)-mestre, mínimo/máximo.
• Calibração inapropriada (não cobrindo o intervalo de operação) ou uso inapropriado do(s) padrão(ões)-
mestre
• Instrumento de baixa qualidade – quanto ao projeto ou quanto à conformidade de manufatura.
• Projeto do instrumento não robusto ou método não robusto
• Dispositivo de medição errado para aquela aplicação
• Método de medição diferente – ajuste, carga, aperto/fixação, técnica operacional
• Deformação/distorção (da peça ou do dispositivo de medição) variando com o tamanho da peça
• Ambiente – temperatura, umidade, vibração, limpeza
• Violação de alguma premissa – erro na aplicação de uma constante (valor constante)
• Aplicação – tamanho da peça, posição, habilidade do operador, fadiga, erro de observação (legibibilidade,
paralaxe)
Realização do Estudo de Linearidade
1) Selecionar g ≥ 5 peças cujas medidas, devido à variação do processo, cobrem o intervalo de operação do
dispositivo de medição.
2) Ter cada peça medida por uma inspeção dimensional para determinar seus valores de referência e para
confirmar se o intervalo de operação do dispositivo de medição em pauta foi completamente coberto.
3) Ter cada peça medida m ≥ 10 vezes no dispositivo em questão, por um dos operadores que normalmente
usam tal dispositivo de medição.
• Selecionar as peças aleatoriamente para minimizar a possibilidade de que o avaliador relembre a tendência
durante a realização das medições.
4) Calcular a tendência de cada peça para cada medição, e também, as médias das tendências para cada peça.
tendênciai,j = xi,j – (valor de referência)i
5) Plotar, num gráfico de linhas, as tendências e as médias das tendências em relação aos valores de
referência.
6) Calcular e desenhar a linha de melhor ajuste, bem como, desenhar a faixa de confiança daquela linha,
utilizando as seguintes equações:
Para a linha de melhor ajuste, usar: = axi + b
Onde
xi = valor de referência
= média da tendências
________
tendênciai
=
∑=
m
j
jtendênciai
1
,
m
__
yi
__
yi

10. 10
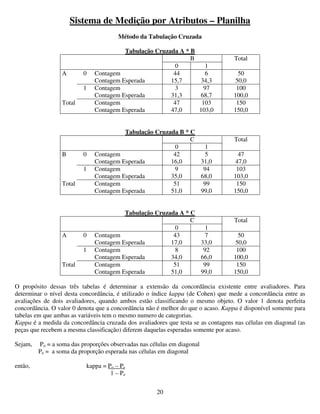
Para um dado x0, a faixa de confiança com nível α40
é:
onde
Limite inferior: b + ax0 -
Limite superior: b + ax0 +
7) traçar alinha de “tendência = 0” e analisar o gráfico, buscando indicações de causas especiais e verificando
a aceitação da linearidade.
Para linearidade do sistema de medição ser aceitável, a linha de “tendência = 0” deve estar inteiramente
contida na faixa de confiança da linha de melhor ajuste.
8) Se a análise gráfica indica que a linearidade do sistema de medição é aceitável, então a seguinte hipótese
deve ser verdadeira:
H0: a = 0 inclinação da reta = 0
não rejeitar se,
Σxy – (1/gmΣxΣy)
Σx2
– 1/gm(Σx)2a = = inclinação da reta
b = y – ax = interseção da reta com o eixo vertical
Σy2
i - bΣyi - aΣxiyi
gm - 2
S =
1
gm
(x0 – x)2
Σ (xi – x)2
( +
) s
½
[ ]tgm-2,1-α/2
1
gm
(x0 – x)2
Σ (xi – x)2
( +
) s
½
[ ]tgm-2,1-α/2
| t | =
| a |
≤ tgm-2,1-α/2
Σ (xj – x)2
s
[ ]

11. 11
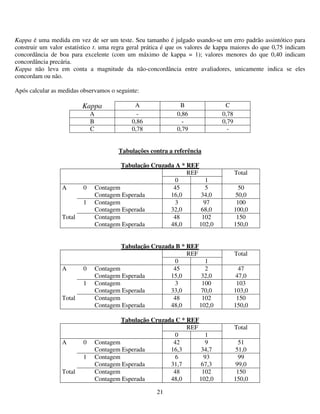
Se a hipótese anteriormente apresentada for verdadeira, então o sistema de medição tem a mesma tendência
para todos os valores de referência. Para a linearidade ser aceitável, estas tendências devem ser zero.
H0 : b = 0 Interseção da linha com o eixo vertical (da tendência) = 0
não rejeitar se:
5 – Estabilidade
Estabilidade (ou Deslocamento lento e Gradual) é a variação total nas medições obtidas com um sistema de
medição aplicado sobre o mesmo padrão-mestre ou peças quando medindo uma única característica no decorrer de
um período de tempo prolongado. Isto é , estabilidade é a variação da tendência ao longo do tempo.
As causas possíveis da instabilidade são:
• Instrumento necessita calibração, reduzir o intervalo de tempo entre calibrações
• Desgaste do instrumento, equipamento, ou dispositivo de fixação
• Envelhecimento normal ou obsolescência
• Manutenção precária – ar, energia, hidráulica, filtros, corrosão, ferrugem, limpeza
• Padrão mestre desgastado ou danificado, erro padrão mestre
• Instrumento de baixa qualidade – quanto ao projeto ou quanto à conformidade de manufatura
• Projeto do instrumento não robusto ou método não robusto
• Método de medição diferente – ajuste, carga, aperto/fixação, técnica de operação
• Deformação/distorção (da peça ou do dispositivo de medição)
• Deslocamento dos parâmetros ambientais lento e gradual – temperatura, umidade, vibração, limpeza
• Violação de alguma premissa – erro na aplicação de uma constante (valor constante)
• Aplicação – tamanho da peça, posição, habilidade do operador, fadiga, erro de observação (legibibilidade,
paralaxe)
Realização do Estudo de Estabilidade
1) obter um padrão e estabelecer seu valor de referência contra um padrão rastreável. Caso não haja
disponibilidade de um padrão, selecionar uma peça de produção que se situe no meio dos intervalos de
medições feita na produção, denominando-a de peça-padrão para efeito de analise da estabilidade. O valor
de referência conhecido não é necessário para acompanhar a estabilidade do sistema de medição.
2) Medir a peça padrão periodicamente (diariamente, semanalmente) de três a cinco vezes. O tamanho da
amostra e a sua freqüência devem se basear no conhecimento do sistema de medição. Alguns fatores são:
quão freqüentes é necessária a re-calibração, quão freqüente é necessário o reparo, quão freqüentemente o
sistema de medição é utilizado, e quão estressantes são as condições operacionais. As leituras devem ser
tomadas em diferentes momentos para representarem quando o sistema de medição está realmente sendo
usado. Isto levará em conta a preparação/início de corrida, o ambiente ou outros fatores que podem variar
durante o dia.
3) Plotar os dados numa carta de controle & R ou & S, mantendo a seqüência em função do tempo.
| t | =
| b |
≤ tgm-2,1-α/2
[ ]1
gm
x2
Σ (xi – x)2
+
__
X
__
X

12. 12
4) Estabelecer os limites de controle e avaliar as condições de processo instável ou ‘ fora de controle’. Por
meio da análise convencional de uma carta de controle.
5) Além das análises das cartas de controle convencionais, não há análise numérica especifica para a
instabilidade. Não há indicador para estabilidade.
Além disso, o desvio padrão das medições pode ser usado como uma aproximação para a repetitividade do
sistema de medição. A comparação entre o desvio padrão das medições e a repetitividade serve para
determinar se a repetitividade do sistema de medição é adequada para tal aplicação.
Se o processo de medição for estável, os dados podem ser usados para determinar a tendência do sistema de
medição.
6– Repetitividade e Reprodutibilidade (R&R)
Repetitividade: Tradicionalmente a repetitividade é conhecida como a variabilidade “de um único avaliador”. A
repetitividade é a variação das medições obtidas com um instrumento de medição, usado várias vezes por um
avaliador, enquanto medindo uma mesma característica de uma mesma peça. Ela é a variação inerente ao
equipamento, ou é a capabilidade do próprio equipamento. A repetitividade é comumente denominada como sendo
a variação do equipamento (VE), embora isto seja uma idéia errada. De fato, a repetitividade é uma variação de
causa comum (erro aleatório) decorrente de sucessivas medições feitas sob condições definidas. O melhor termo
para designar repetitividade é variação dentro do sistema, pois as condições de medição são fixas e definidas – são
entidades mantidas fixas: peça, instrumento, padrão, método,operador, ambiente, e certas premissas. Além do mais,
tal e qual a variação dentro do equipamento, a repetitividade incluirá também todas as variações dentro
provenientes de qualquer condição do modelo de erro.
As causas possíveis de uma repetitividade precária são:
• Variação dentro da peça (amostra): forma, posição, acabamento superficial, conicidade, consistência da
amostra
• Variação dentro do instrumento: reparo, desgaste, falha do equipamento ou dispositivo de fixação, baixa
qualidade ou manutenção precária.
• Variação dentro do padrão: qualidade, classe, desgaste
• Variação dentro do método: variação no ajuste, na técnica operacional, no zerar o equipamento, na fixação
da peça, no aperto do dispositivo, na densidade de pontos (a densidade de pontos é a freqüência de pontos
de medição numa determinada área).
• Variação dentro do avaliador: técnica, posição, falta de experiência, habilidade de manipulação,
treinamento de manuseio, sentimento/sensibilidade pessoal, fadiga.
• Variação dentro do ambiente: pequena flutuações cíclicas na temperatura, umidade, vibração, iluminação,
limpeza.
• Violação de alguma premissa – estabilidade, operação apropriada.
• Projeto do instrumento não robusto ou método não robusto, uniformidade precária.
• Dispositivo de medição errado para aquela aplicação.
• Deformação/distorção (da peça ou do dispositivo de medição), falta de rigidez
• Aplicação – tamanho da peça, posição, habilidade do operador, fadiga, erro de observação (legibibilidade,
paralaxe)
Reprodutibilidade: Tradicionalmente a reprodutibilidade é conhecida como variabilidade “entre avaliadores”. A
reprodutibilidade é tipicamente definida como a variação das médias das medições feitas por diferentes
avaliadores, utilizando um mesmo instrumento de medição, enquanto medindo uma mesma característica de
uma mesma peça. Isto é muito real para instrumentos manuais influenciados pela habilidade do operador.
Contudo, não é real para processos de medição em que o operador não se constitui na maior fonte de variação

13. 13
(exemplo: sistemas automáticos). Por esta razão, a reprodutibilidade é denominada como a variação das médias
entre sistemas, ou entre condições de medição.
A definição da ASTM vai além disto, potencialmente ela inclui não somente os diferentes avaliadores, mas
também os diferentes dispositivos de medição, laboratórios, e ambientes (temperatura, umidade), bem como inclui
a repetitividade no cálculo da reprodutibilidade.
As causas possíveis para erro de reprodutibilidade são:
• Variação entre peças (amostras): diferenças de média quando medindo tipos de peças A, B, C, etc., usando
o mesmo instrumento, os mesmos operadores, e o mesmo método.
• Variação entre instrumentos: diferença de média usando instrumentos A, B, C, etc., para as mesmas peças,
mesmos operadores, e mesmo ambiente.
Nota: neste estudo, o erro de reprodutibilidade é geralmente confundido com o erro do método e/ou com o
erro do operador.
• Variação entre padrões: influência média de diferentes conjunto de padrões no processo de medição.
• Variação entre métodos: diferença de médias causada pelo variar das densidade de pontos, sistemas manual
vs. Automático, métodos para zerar o equipamento, métodos para fixação da peça, métodos de
aperto/fixação, etc.
• Variação entre avaliadores (operadores): Diferenças de média entre os avaliadores A,B,C, etc., causada por
treinamento, técnica operacional, habilidade e experiência. Este é o estudo recomendado para a qualificação
do produto e do processo, bem como para a qualificação do instrumento de medição manual.
• Variação entre ambientes: diferença de médias em medições feitas no decorrer do tempo 1, 2, 3, etc.,
causada pelos ciclos ambientais; este é o estudo mais comum para os sistemas altamente automatizados,
quando da qualificação do produto e do processo.
• Violação de alguma premissa no estudo
• Projeto do instrumento não robusto ou método não robusto
• Eficácia do treinamento do operador
• Aplicação – tamanho da peça, posição, habilidade do operador, fadiga, erro de observação (legibibilidade,
paralaxe)
R & R do Dispositivo de Medição
O R&R do dispositivo de medição é uma estimativa da variação combinada da repetitividade e da
reprodutibilidade. Dito de outra forma, o R&R é a variância resultante da soma das variâncias dentro do sistema e
entre sistemas.
Realização do Estudo de Repetitividade e Reprodutibilidade
O estudo dos dispositivos de Medição por variáveis pode serrealizado com diferentes técnicas. Três métodos
aceitáveis serão exposto:
• Método da Amplitude
• Método da Amplitude e Média (incluindo o método da Carta de Controle)
• Método da ANOVA
Método da Média e Amplitude
O método da Média e Amplitude ( & R ) é uma abordagem que fornece uma estimativa da repetitividade e
reprodutibilidade de um sistema de medição.
Embora a quantidade de avaliadores, de medições repetidas, e de peças possam variar, a discussão a seguir
apresentada representa as condições ótimas de realização do estudo.
1) Obter uma amostra de n > 5 peças que representa o intervalo real ou esperado da variação do processo.
2) Identificar as peças com um número de 1 até n, de modo que os números de identificação das peças sejam
visíveis aos avaliadores
__
X

14. 14
3) Calibrar o dispositivo de medição, caso isto seja parte dos procedimentos usuais do sistema de medição.
Obter do primeiro avaliador as medidas das n peças feitas em ordem aleatória e registrar os resultados na
planilha.
4) Obter dos outros avaliadores as medidas as medidas das mesmas n peças, feitas de maneira que um
avaliador não conheça a leitura dos demais; registrar os resultados na planilha.
5) Repetir o ciclo de medições utilizando uma ordem aleatória de medição diferente. Registrar os dados na
planilha.
6) Em caso de peças de tamanho grande ou em caso de ser impossível dispor de todas as peças
simultaneamente, os passos 4 e 5 podem ser substituídos por:
• Obter do primeiro avaliador a medida da primeira peça e registrar, obter do segundo avaliador a medida da
mesma peça e assim sucessivamente.
7) Um método alternativo pode ser usado em caso de os avaliadores trabalharem em diferentes turnos. Obter
do primeiro avaliador as medidas das n peças e registra-la. Em seguida obter do mesmo avaliador as leituras
das n peças em ordem seqüencial diferente para os outros ciclos. Repetir o procedimento para os outros
avaliadores.
7 – Estudo dos Sistemas de Medição por Atributos
Os sistemas de medição por atributos constituem a classe de sistemas de medição em que o valor de medição é
único, de um número finito de categorias. Isto contrasta com os sistemas de medição por variáveis que podem gerar
valores numa escala contínua. O mais comum desses sistemas por atributos é o calibrador passa/não passa que
apresenta unicamente dois resultados possíveis. Outros sistemas para atributos, por exemplo: padrões visuais,
podem gerar de cinco a sete categorias distintas, como: muito bom, bom, suficiente, pobre, muito pobre.
Em algumas situações de atributo, não é viável obter uma quantidade suficiente de peças com valores de referência
variáveis. Em tais casos, os riscos de tomar uma decisão errada ou inconsistente podem ser avaliados através da:
• Análise de Teste de Hipóteses
• Teoria de Detecção do Sinal
Devido que esses métodos não quantificam a variabilidade do sistema de medição, eles deverão ser usados somente
com o consentimento do cliente. A escolha e o uso de tais técnicas devem se basear:
• Em boas práticas estatísticas
• Na compreensão das fontes potenciais de variação que podem afetar o produto e os processos de medição
• No efeito de uma decisão incorreta sobre os processos seguintes e sobre o cliente final
As fontes de variação dos sistemas por atributos devem ser minimizadas pelo uso dos resultados de fatores
humanos e da pesquisa ergonômica.

15. 15
Se a peça estiver na Zona (I) ela deve ser designada com o sinal (-), todas estão reprovadas. Se a peça estiver na
Zona (II), deve ser designada com o sinal (x), poderá haver peças aprovadas e peças reprovadas, e por fim se a peça
estiver na Zona (III), deve ser designada com o sinal (+), todas estão aprovadas.
8 – Práticas para Sistemas de Medição Complexos ou Não-Replicáveis
O foco do MSA é o conjunto de medições que permitem replicar as leituras sobre cada uma das peças. Porém, nem
todos os sistemas de medição tem esta característica; por exemplo:
• Sistemas de medição destrutiva
• Sistemas onde a peça se modifica no uso ou no teste; exemplo: teste de dinamômetro de motor ou
transmissão (caixa de câmbio)
Tipos de Medições Destrutivas ou Não replicáveis:
• Dureza
• Ensaios de Tração/Compressão
• Charpy
• Análise no espectofotômetro
• Etc.
Para estes tipos de medições podemos usar o sistema de espécimes divididos (S4) a análise é feita por uma carta de
amplitudes para acompanhar a consistência das medições (confundida com a consistência dentro de um mesmo
lote).
9 – Análises dos Resultados
Os resultados devem ser avaliados para determinar se o aparato de medição é aceitável para sua pretendida
aplicação. Um sistema de medição deve estar estável antes de qualquer análise adicional ser considerada válida.
Erro de Localização – O erro de localização é normalmente determinado pela análise da tendência e da
linearidade.
Em geral, o erro de tendência ou de linearidade de um sistema de medição é inaceitável se forem
significativamente diferentes de zero ou excederem o erro máximo permissível estabelecido pelo procedimento de
calibração do dispositivo de medição. Em tais casos, o sistema de medição deve ser recalibrado, ou uma correção
compensatória deverá ser aplicada para minimizar este erro.
No geral o estudo deve ser considerado aceitável se os resultados se encontrarem dentro do intervalo de confiança.
Erro de Dispersão – Os critérios para verificar se a variabilidade do sistema de medição é satisfatória dependem
da porcentagem em relação à variabilidade do processo de produção, ou ainda, dependem da porcentagem da
tolerância da peça que é consumida pela variação do sistema de medição. Os critérios de aceitação final para
específicos sistemas de medição dependem do ambiente onde vai operar o sistema de medição e do seu propósito.
Os critérios de aceitação final devem ser aprovados pelo cliente.
Para sistemas de medição cujo propósito é analisar um processo de medição, uma regra prática geral para a sua
aceitação vai a seguir:
• Erro menor que 10% - sistema de medição geralmente considerado como aceitável.
• Erro entre 10% e 30% - o sistema de medição pode ser aceito com base na importância de sua aplicação, no
custo do aparato de medição, no custo do reparo, etc.
• Erro acima de 30% - sistema de medição considerado como não-aceitável, sendo que todo o esforço deve
ser feito para melhora-lo.

16. 16
Além disso, quanto ao número de distintas categorias (ndc), o processo pode ser dividido pelo sistema de medição
em uma certa quantidade de partes que deve ser igual ou maior a 5.

17. 17
Análise gráfica dos resultados
Carta de Médias – As médias de múltiplas leituras feitas por cada avaliadores, sobre cada uma das peças são
plotadas pelo avaliador, que marca no eixo das abscissas o número de identificação da peça. Este gráfico pode
auxiliar a determinação da consistência entre avaliadores.
A média das médias e os limites de controle (calculados com a amplitude média), são também traçados. A carta de
médias resultantes nos esclarece e informa sobre “a possibilidade de uso” do sistema de medição.
A área situada entre os limites de controle representa a sensibilidade de medição (“ruído”). Caso o conjunto de
peças usado no estudo represente a variação do processo, aproximadamente metade (ou mais) das médias se
situarão acima ou abaixo desses limites de controle. Se os dados mostrarem esta configuração gráfica, então o
sistema de medição será adequado para detectar a variação peça-a-peça e o sistema de medição poderá gerar
informações úteis para a análise e controle do processo de produção. Se menos que metade dessas médias
estiverem localizadas além dos limites de controle, então ou o sistema de medição não dispõe de resolução efetiva,
ou a amostra não representa a variação esperada do processo.
Carta de Amplitudes – A carta de controle de amplitudes é utilizada para verificar se um processo está sob
controle. Não interessa quão grande possa ser o erro de medição, os limites de controle incluem aquele erro. Esta é
a razão pela qual se torna necessária a identificação e eliminação das causas especiais de variação, antes de
qualificar um estudo como relevante.
As amplitudes das múltiplas leituras feitas por cada avaliador sobre cada peça são plotadas numa carta de
amplitudes convencional, incluindo-se as marcações da amplitude média e do(s) limite(s) de controle. A partir da
análise dos dados projetados na carta, algumas interpretações úteis podem ser feitas. Se todas as amplitudes
projetadas estiverem sob controle, então todos os avaliadores estarão trabalhando de igual forma, estarão fazendo o
mesmo trabalho.
Se um dos avaliadores estiver fora de controle, então o método por ele utilizado difere do método utilizado pelos
demais.
Se todos os avaliadores tiverem alguma amplitude fora de controle, o sistema de medição mostra-se sensível à
técnica utilizada pelos avaliadores, e portanto necessita algum aperfeiçoamento para poder gerar dados úteis.
A carta de amplitudes auxilia na verificação:
• Do controle estatístico com respeito à repetitividade
• Da consistência do processo de medição entre avaliadores para cada peça.
Carta das Médias
11,850
11,870
11,890
11,910
11,930
11,950
11,970
11,990
Carta das Amplitudes
0,0000
0,0200
0,0400
0,0600
0,0800
0,1000
0,1200

18. 18
Tabela de Distribuição de t (Student)
gl/P 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,10 0,05 0,02 0,01 0,001
01 0,158 0,325 0,510 0,727 1,000 1,376 1,963 3,078 6,314 12,706 31,821 63,657 636,619
02 0,142 0,289 0,445 0,617 0,816 1,061 1,386 1,886 2,920 4,303 6,965 9,925 31,598
03 0,137 0,277 0,424 0,584 0,765 0,978 1,250 1,638 2,353 3,182 4,541 5,541 12,924
04 0,134 0,271 0,414 0,569 0,741 0,941 1,190 1,533 2,132 2,776 3,747 4,604 8,610
05 0,132 0,267 0,408 0,559 0,727 0,920 1,156 1,476 2,015 2,571 3,365 4,032 6,869
06 0,131 0,265 0,404 0,553 0,718 0,906 1,134 1,440 1,943 2,447 3,143 3,707 5,959
07 0,130 0,263 0,402 0,549 0,711 0,896 1,119 1,415 1,895 2,365 2,365 3,499 5,408
08 0,130 0,262 0,399 0,546 0,706 0,889 1,108 1,397 1,860 2,306 2,896 3,355 5,041
09 0,129 0,261 0,398 0,543 0,703 0,883 1,100 1,383 1,833 2,262 2,821 3,250 4,781
10 0,129 0,260 0,397 0,542 0,700 0,879 1,093 1,372 1,812 2,228 2,764 3,169 4,587
11 0,129 0,260 0,396 0,540 0,697 0,876 1,088 1,363 1,796 2,201 2,718 3,106 4,437
12 0,128 0,259 0,395 0,539 0,695 0,873 1,083 1,356 1,782 2,179 2,681 3,055 4,318
13 0,128 0,259 0,394 0,538 0,694 0,870 1,079 1,350 1,771 2,160 2,650 3,012 4,221
14 0,128 0,258 0,393 0,537 0,692 0,868 1,076 1,345 1,761 2,145 2,624 2,977 4,140
15 0,128 0,258 0,393 0,536 0,691 0,866 1,074 1,341 1,753 2,131 2,602 2,947 4,073
16 0,128 0,258 0,392 0,535 0,690 0,865 1,071 1,337 1,746 2,120 2,583 2,921 4,015
17 0,128 0,257 0,392 0,534 0,689 0,863 1,069 1,333 1,740 2,110 2,567 2,898 3,965
18 0,127 0,257 0,392 0,534 0,688 0,862 1,067 1,330 1,734 2,101 2,552 2,878 3,922
19 0,127 0,257 0,391 0,533 0,688 0,861 1,066 1,328 1,729 2,093 2,539 2,861 3,883
20 0,127 0,257 0,391 0,533 0,687 0,860 1,064 1,325 1,725 2,086 2,528 2,845 3,850
21 0,127 0,257 0,391 0,532 0,686 0,859 1,063 1,323 1,721 2,080 2,518 2,831 3,819
22 0,127 0,256 0,390 0,532 0,686 0,858 1,061 1,321 1,717 2,074 2,508 2,819 3,792
23 0,127 0,256 0,390 0,532 0,685 0,858 1,060 1,319 1,714 2,069 2,500 2,807 3,767
24 0,127 0,256 0,390 0,531 0,685 0,857 1,059 1,318 1,711 2,064 2,492 2,797 3,745
25 0,127 0,256 0,390 0,531 0,684 0,856 1,058 1,316 1,708 2,060 2,485 2,787 3,726
26 0,127 0,256 0,390 0,531 0,684 0,856 1,058 1,315 1,706 2,056 2,479 2,779 3,707
27 0,127 0,256 0,389 0,531 0,684 0,856 1,057 1,314 1,703 2,052 2,473 2,771 3,690
28 0,127 0,256 0,389 0,530 0,683 0,856 1,056 1,313 1,701 2,048 2,467 2,763 3,674
29 0,127 0,256 0,389 0,530 0,683 0,854 1,055 1,311 1,699 2,045 2,462 2,756 3,659
30 0,127 0,256 0,389 0,530 0,683 0,854 1,055 1,310 1,697 2,042 2,457 2,750 3,646
40 0,126 0,255 0,388 0,529 0,681 0,851 1,050 1,303 1,684 2,021 2,423 2,704 3,551
60 0,126 0,254 0,387 0,527 0,679 0,848 1,046 1,296 1,671 2,000 2,390 2,660 3,460
120 0,126 0,254 0,386 0,526 0,677 0,845 1,041 1,289 1,658 1,980 2,358 2,617 3,373
i 0,126 0,253 0,385 0,524 0,674 0,842 1,036 1,282 1,645 1,960 2,326 2,576 3,291
i = infinito

19. 19
Sistema de Medição por Atributos – Dados
Peça A - 1 A - 2 A - 3 B - 1 B - 2 B - 3 C - 1 C - 2 C – 3 Refer. Valor de Ref. Código
1 1 1 1 1 1 1 1 1 1 1 0,476901 +
2 1 1 1 1 1 1 1 1 1 1 0,509015 +
3 0 0 0 0 0 0 0 0 0 0 0,576459 -
4 0 0 0 0 0 0 0 0 0 0 0,566152 -
5 0 0 0 0 0 0 0 0 0 0 0,570360 -
6 1 1 0 1 1 0 1 0 0 1 0,544951 x
7 1 1 1 1 1 1 1 0 1 1 0,465454 x
8 1 1 1 1 1 1 1 1 1 1 0,502295 +
9 0 0 0 0 0 0 0 0 0 0 0,437817 -
10 1 1 1 1 1 1 1 1 1 1 0,515573 +
11 1 1 1 1 1 1 1 1 1 1 0,488905 +
12 0 0 0 0 0 0 0 1 0 0 0,559918 x
13 1 1 1 1 1 1 1 1 1 1 0,542704 +
14 1 1 0 1 1 1 1 0 0 1 0,454518 x
15 1 1 1 1 1 1 1 1 1 1 0,517377 +
16 1 1 1 1 1 1 1 1 1 1 0,531939 +
17 1 1 1 1 1 1 1 1 1 1 0,519694 +
18 1 1 1 1 1 1 1 1 1 1 0,484167 +
19 1 1 1 1 1 1 1 1 1 1 0,520496 +
20 1 1 1 1 1 1 1 1 1 1 0,477236 +
21 1 1 0 1 0 1 0 1 0 1 0,452310 x
22 0 0 1 0 1 0 1 1 0 0 0,545604 x
23 1 1 1 1 1 1 1 1 1 1 0,529065 +
24 1 1 1 1 1 1 1 1 1 1 0,514192 +
25 0 0 0 0 0 0 0 0 0 0 0,599581 -
26 0 1 0 0 0 0 0 0 1 0 0,547204 x
27 1 1 1 1 1 1 1 1 1 1 0,502436 +
28 1 1 1 1 1 1 1 1 1 1 0,521642 +
29 1 1 1 1 1 1 1 1 1 1 0,523754 +
30 0 0 0 0 0 1 0 0 0 0 0,561457 x
31 1 1 1 1 1 1 1 1 1 1 0,503091 +
32 1 1 1 1 1 1 1 1 1 1 0,505850 +
33 1 1 1 1 1 1 1 1 1 1 0,487613 +
34 0 0 1 0 0 1 0 1 1 0 0,449696 x
35 1 1 1 1 1 1 1 1 1 1 0,498698 +
36 1 1 0 1 1 1 1 0 1 1 0,543077 x
37 0 0 0 0 0 0 0 0 0 0 0,409238 -
38 1 1 1 1 1 1 1 1 1 1 0,488184 +
39 0 0 0 0 0 0 0 0 0 0 0,427687 -
40 1 1 1 1 1 1 1 1 1 1 0,501132 +
41 1 1 1 1 1 1 1 1 1 1 0,513779 +
42 0 0 0 0 0 0 0 0 0 0 0,566575 -
43 1 0 1 1 1 1 1 1 0 1 0,462410 x
44 1 1 1 1 1 1 1 1 1 1 0,470832 +
45 0 0 0 0 0 0 0 0 0 0 0,412453 -
46 1 1 1 1 1 1 1 1 1 1 0,493441 +
47 1 1 1 1 1 1 1 1 1 1 0,486379 +
48 0 0 0 0 0 0 0 0 0 0 0,587893 -
49 1 1 1 1 1 1 1 1 1 1 0,483803 +
50 0 0 0 0 0 0 0 0 0 0 0,446697 -

20. 20
Sistema de Medição por Atributos – Planilha
Método da Tabulação Cruzada
Tabulação Cruzada A * B
B
0 1
Total
A 0 Contagem
Contagem Esperada
44
15,7
6
34,3
50
50,0
1 Contagem
Contagem Esperada
3
31,3
97
68,7
100
100,0
Total Contagem
Contagem Esperada
47
47,0
103
103,0
150
150,0
Tabulação Cruzada B * C
C
0 1
Total
B 0 Contagem
Contagem Esperada
42
16,0
5
31,0
47
47,0
1 Contagem
Contagem Esperada
9
35,0
94
68,0
103
103,0
Total Contagem
Contagem Esperada
51
51,0
99
99,0
150
150,0
Tabulação Cruzada A * C
C
0 1
Total
A 0 Contagem
Contagem Esperada
43
17,0
7
33,0
50
50,0
1 Contagem
Contagem Esperada
8
34,0
92
66,0
100
100,0
Total Contagem
Contagem Esperada
51
51,0
99
99,0
150
150,0
O propósito dessas três tabelas é determinar a extensão da concordância existente entre avaliadores. Para
determinar o nível desta concordância, é utilizado o índice kappa (de Cohen) que mede a concordância entre as
avaliações de dois avaliadores, quando ambos estão classificando o mesmo objeto. O valor 1 denota perfeita
concordância. O valor 0 denota que a concordância não é melhor do que o acaso. Kappa é disponível somente para
tabelas em que ambas as variáveis tem o mesmo numero de categorias.
Kappa é a medida da concordância cruzada dos avaliadores que testa se as contagens nas células em diagonal (as
peças que recebem a mesma classificação) diferem daquelas esperadas somente por acaso.
Sejam, Po = a soma das proporções observadas nas células em diagonal
Pe = a soma da proporção esperada nas células em diagonal
então, kappa = Po – Pe
1 – Pe

21. 21
Kappa é uma medida em vez de ser um teste. Seu tamanho é julgado usando-se um erro padrão assintótico para
construir um valor estatístico t. uma regra geral prática é que os valores de kappa maiores do que 0,75 indicam
concordância de boa para excelente (com um máximo de kappa = 1); valores menores do que 0,40 indicam
concordância precária.
Kappa não leva em conta a magnitude da não-concordância entre avaliadores, unicamente indica se eles
concordam ou não.
Após calcular as medidas observamos o seguinte:
Kappa A B C
A - 0,86 0,78
B 0,86 - 0,79
C 0,78 0,79 -
Tabulações contra a referência
Tabulação Cruzada A * REF
REF
0 1
Total
A 0 Contagem
Contagem Esperada
45
16,0
5
34,0
50
50,0
1 Contagem
Contagem Esperada
3
32,0
97
68,0
100
100,0
Total Contagem
Contagem Esperada
48
48,0
102
102,0
150
150,0
Tabulação Cruzada B * REF
REF
0 1
Total
A 0 Contagem
Contagem Esperada
45
15,0
2
32,0
47
47,0
1 Contagem
Contagem Esperada
3
33,0
100
70,0
103
103,0
Total Contagem
Contagem Esperada
48
48,0
102
102,0
150
150,0
Tabulação Cruzada C * REF
REF
0 1
Total
A 0 Contagem
Contagem Esperada
42
16,3
9
34,7
51
51,0
1 Contagem
Contagem Esperada
6
31,7
93
67,3
99
99,0
Total Contagem
Contagem Esperada
48
48,0
102
102,0
150
150,0

22. 22
Cálculo da medida kappa para determinar a concordância de cada avaliador contra a decisão de referência:
A B C
Kappa 0,88 0,92 0,77
Cálculo do índice kappa.
Contagem esperada = Total linha x Total coluna
Total Geral
Kappa = ∑ Vo ( ) - ∑ Ve ( )
∑ Ve ( )
onde: Vo = Valor obtido
Ve = Valor esperado

23. 23
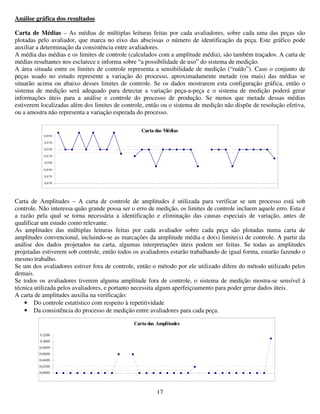
Relatório de Repetitividade e Reprodutibilidade de um Dispositivo de
Medição
Dados:
PeçaAvaliador/
Ciclos 1 2 3 4 5 6 7 8 9 10
Média
A 1 0,29 -0,56 1,34 0,47 -0,80 0,02 0,59 -0,31 2,26 -1,36
2 0,41 -0,68 1,17 0,50 -0,92 -0,11 0,75 -0,20 1,99 -1,25
3 0,64 -0,58 1,27 0,64 -0,84 -0,21 0,66 -0,17 2,01 -1,31
Média
0,447 -0,607 1,260 0,837 -0,853 -0,100 0,667 -0,227 2,087 -1,307 0,19
Amplitude
0,35 0,12 0,17 0,17 0,12 0,23 0,16 0,14 0,27 0,11 0,1
B 1 0,08 -0,47 1,19 0,01 -0,56 -0,20 0,47 -0,63 1,80 -1,68
2 0,25 -1,22 0,94 1,03 -1,20 0,22 0,55 0,08 2,12 -1,62
3 0,07 -0,68 1,34 0,20 -1,28 0,06 0,83 -0,34 2,19 -1,50
Média
0,133 -0,790 1,157 0,413 -1,013 0,027 0,617 -0,297 2,037 -1,600 0,06
Amplitude
0,18 0,75 0,40 1,02 0,72 0,42 0,36 0,71 0,39 0,18 0,5
C 1 0,04 -1,38 0,88 0,14 -1,46 -0,29 0,02 -0,46 1,77 -1,49
2 -0,11 -1,13 1,09 0,20 -1,07 -0,67 0,01 -0,56 1,45 -1,77
3 -0,15 -0,96 0,67 0,11 -1,45 -0,49 0,21 -0,49 1,87 -2,16
Média
0,073 -1,157 0,880 0,150 -1,327 -0,483 0,080 -0,503 1,697 -1,807 -0,25
Amplitude
0,19 0,42 0,42 0,09 0,39 0,38 0,20 0,10 0,42 0,67 0,3
Média por Peça
0,169 -0,851 1,099 0,367 -1,064 -0,186 0,454 -0,342 1,940 -1,571
0,00
3,5
0,34
0,4446
*D4 = 3,27 para 2 medições repetidas e 2,58 para 3 medições repetidas. LSCR representa o limite de controle para
os R’s, individualmente considerados. Circular aqueles que se situam além deste limite. Identificar a causa e
corrigi-la. O mesmo avaliador deve repetir estas leituras sobre as mesmas peças originalmente usadas, ou descartar
tais leituras. Refazer então todos os cálculos de médias, do e do LSCR com as leituras restantes.
R = R =
Rc=
Xc=
Xa=
Ra=
Xb=
Rb=
X =
Rp =
([Ra= 0,184 ] + [Rb= 0,513 ] + [Rc= 0,328 ]) / [#N°Avaliadores= 3 ]
XDIF = [Max X =0,1903 ] -
-
XDIF =
[Min X = -0,2543 ]
=
*LSCR =[R = 0,3417 ] X [D4 = 2,58 ] = 0,8816
R ,

24. 24
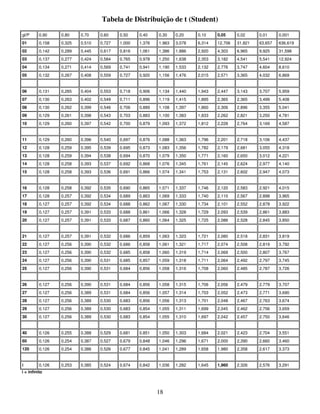
Relatório de Repetitividade e Reprodutibilidade de um Dispositivo de
Medição
Análise na Unidade de Medição % sobre a Variação Total (VT)
Repetitividade – Variação do equipamento (VE)
VE = x K1
N° de
Medições
Repetidas K1 % VE = 100 [VE/VT]
= 0,3417 x 0,5908 2 0,8862 = 100 [0,20188 / 1,14610]
= 0,20188 3 0,5908 = 17,62 %
Reprodutibilidade – Variação entre Avaliadores (VA)
VA = ( K2 )2
– ( VE2
/(nr)) %VA = 100 [VA/VT]
= (0,4446 x0,5231) – (0,20188 2
/ (10x3)) = 100 [ 0,22963 / 1,14610 ]
= 0,22963
N° de
Avaliadores
2 3 = 20,04 %
n = n° de peças r = n° de medições repetidas
K2 0,7071 0,5231
Repetitividade & Reprodutibilidade ( R & R )
R&R = VE2
+ VA2
%R&R = 100 [ R&R / VT]
= (0,201882
+0,229632
)
N° de
Peças K3 = 100 [0,30575 / 1,14610 ]
= 0,30575 2 0,7071 = 26,68 %
Variação da Peça (VP)
3 0,5231
VP = Rp x K3 4 0,4467 %VP = 100 [ VP / VT ]
= 3,5111x 0,3146 5 0,4030 = 100 [ 1,10456 / 1,14610]
= 1,10456 6 0,3742 = 96,38 %
Variação Total (VT)
7 0,3534
VT = R&R2
+ VP2
8 0,3375 ndc = 1,41 ( VP / R&R )
= (0,305752
+1,104562
) 9 0,3249 = 1,41 (1,10456 / 0,30575)
= 1,14610 10 0,3146 = 5,094 ~ 5
R
XDIF x

25. 25