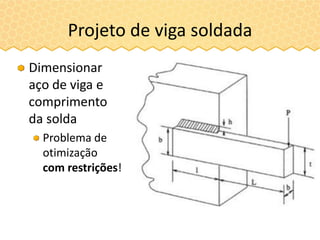
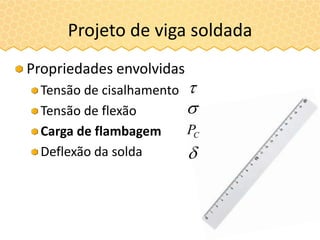
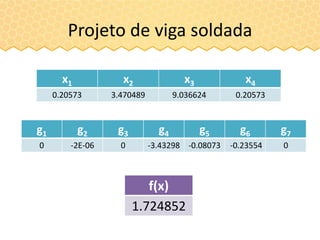
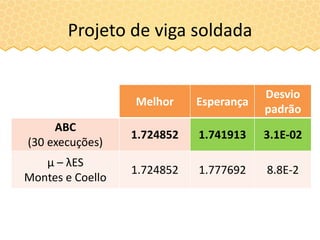
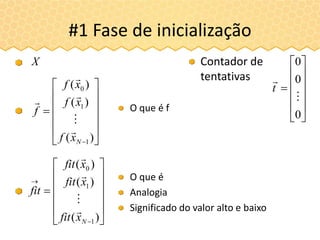
O documento descreve a inteligência de enxames e o algoritmo de otimização ABC (Artificial Bee Colony), inspirado no comportamento das abelhas. O ABC simula uma colônia artificial de abelhas e usa estratégias como exploração aleatória de fontes de alimento e compartilhamento de informações para iterativamente melhorar soluções a problemas de otimização. O algoritmo consiste em fases de abelhas empregadas, observadoras e exploradoras para modelar a comunicação e cooperação entre abelhas.



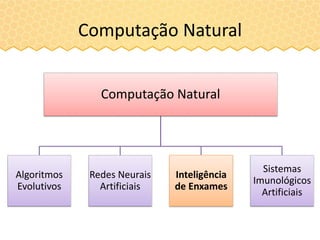



























![Problema de Otimização
Local
Sem restrições
Sabemos de antemão que o vetor ótimo é [0 0]T
Problema
Minimizar f(x) = x1
2 + x2
2 -5≤x1,x2≤5](https://image.slidesharecdn.com/boa2inteligenciadeenxames-abelhas-190106173323/85/Inteligencia-de-Enxames-Abelhas-42-320.jpg)



![Substituir uma das coordenadas de por
Valores sorteados Possibilidades
k ∈ {1,2}
i ∈ {0,1}
Φ ∈ [-1,1]
Obter uma nova fonte (solução candidata) vizinha de
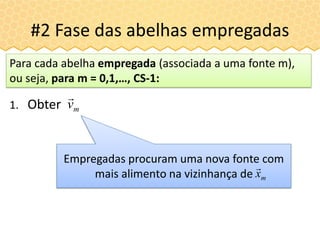
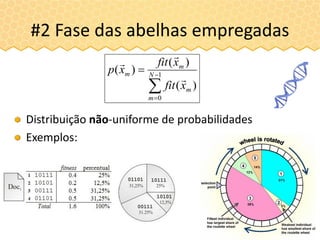
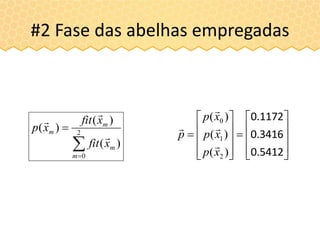
#2 Fase das abelhas empregadas
1ª abelha empregada (1ª fonte de alimento m=0)
kimimimimi xxxv
2.5644-
1.4112
0x
0x
Escolher aleatoriamente
k (fonte != m), i e Φ
0x
0v
](https://image.slidesharecdn.com/boa2inteligenciadeenxames-abelhas-190106173323/85/Inteligencia-de-Enxames-Abelhas-46-320.jpg)
![Valores sorteados Possibilidades
k=1 k ∈ {1,2}
i=0 i ∈ {0,1}
Φ = 0.8050 Φ ∈ [-1,1]
Substituir uma das coordenadas de por
Obter uma nova fonte (solução candidata) vizinha de
#2 Fase das abelhas empregadas
1ª abelha empregada (1ª fonte de alimento m=0)
kimimimimi xxxv
2.5644-
1.4112
0x
0x
Escolher aleatoriamente
k (fonte != m), i e Φ
0x
0v
](https://image.slidesharecdn.com/boa2inteligenciadeenxames-abelhas-190106173323/85/Inteligencia-de-Enxames-Abelhas-47-320.jpg)












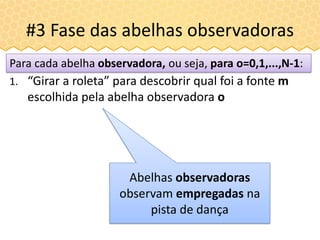
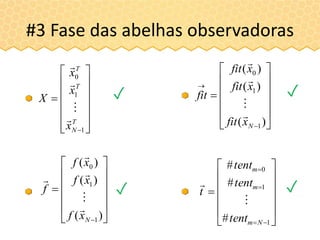
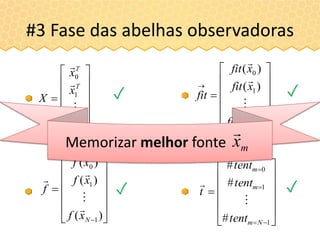
![#3 Fase das abelhas observadoras
1.0323-0.0348
1.43380.1722
2.5644-1.4112
X
1.0669
2.0855
8.5678
f
0.4828
0.3241
0.1045
fit
0
0
1
t
✓
✓
✓
✓
Melhor fonte:
(ótimo é [0 0]T )
T
x 1.0323-0.03482
](https://image.slidesharecdn.com/boa2inteligenciadeenxames-abelhas-190106173323/85/Inteligencia-de-Enxames-Abelhas-61-320.jpg)