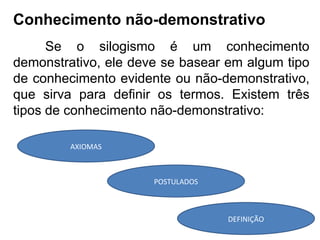
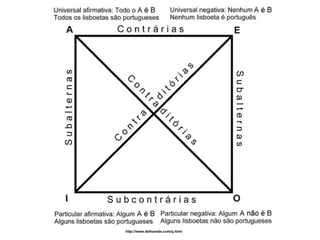
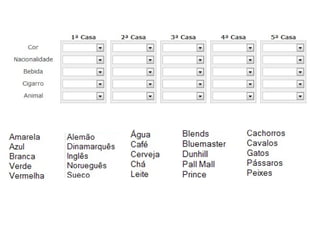
O documento discute a lógica formal desenvolvida por Aristóteles como estrutura do pensamento racional. Aristóteles criticou a dialética de Platão por não lidar com verdades demonstráveis, desenvolvendo regras fixas para o raciocínio lógico através da teoria das proposições e do silogismo. O silogismo permite deduzir conclusões a partir de premissas, enquanto a indução e analogia permitem generalizar a partir de casos particulares.

1. Quando você está conversando ou mesmo discutindo com alguém, é comum o emprego da expressão “é lógico!” – quase sempre com o sentido de “é claro” ou “é evidente”. Mas será que é possível determinar as condições para que uma coisa ou um argumento sejam “lógicos”? LÓGICA

2. Lógica: estrutura formal do pensamento Costuma-se definir Lógica como o estudo da estrutura e dos princípios da argumentação, independente de seu conteúdo. Suas origens remontam a Aristóteles, cuja obra inclui a Lógica enquanto estudo da forma e das regras que utilizamos para pensar as coisas; em outras palavras, enquanto estrutura formal do pensamento.

3. Como em outros momentos da elaboração do pensamento aristotélico, a crítica a Platão foi um dos fundamentos a partir do qual Aristóteles desenvolveu a Lógica. Como vimos anteriormente, Platão defendia o diálogo como forma de se atingir o conhecimento. Na dialética platônica, os confrontos surgidos do diálogo permaneciam sempre em aberto, o que possibilitava a apresentação de novos argumentos e, conseqüentemente, uma nova maneira de compreensão das coisas. Seria dessa forma que a Filosofia iria ascendendo em direção ao conhecimento verdadeiro. Porém, a tensão própria do diálogo abria caminho para o relativismo, o que resultava na impossibilidade de se ter certeza sobre aquilo que foi debatido, alcançando-se a verdade numa forma incompleta.

4. Aristóteles via o diálogo como um mero exercício, uma vez que a dialética não lidava com as coisas do mundo (que deveriam ser objeto de estudo), mas apenas com a opinião dos homens sobre as coisas. O conhecimento seguro deveria ter, portanto, outra fonte: o estabelecimento de regras fixas do pensamento, que permitiriam a obtenção de verdades demonstráveis. Nesse sentido, deve-se atentar para a importância do emprego das palavras, que devem ter significados precisos. Daí a necessidade do estudo da linguagem.

5. Teoria das proposições Em seu livro Organon (palavra grega que significa “instrumento”), Aristóteles desenvolveu a teoria das proposições. Toda proposição é o enunciado de um juízo – formulado pelo pensamento – que atribui um predicado a um sujeito. Uma proposição é formada pela união de termos, que são as palavras usadas para designar todas as coisas. O encadeamento dos juízos é chamado de raciocínio.

6. Quando alguém enuncia a proposição “Platão é forte”, os termos “Platão” e “forte” se apresentam unidos por um juízo elaborado pelo pensamento. Esse juízo pode ou não estar adequado à realidade, ou seja: se Platão for realmente forte, o juízo enunciado através da proposição é um juízo verdadeiro. Os termos têm duas propriedades: a extensão (ou alcance) e a compreensão (ou entendimento). Assim, a palavra “árvore” refere-se a um conjunto bastante grande de objetos, ou seja, ao se usar essa palavra, o alcance ou extensão do juízo formulado será o maior possível. A referência a determinada árvore, como um “limoeiro”, por exemplo, limita o alcance do juízo, mas amplia seu entendimento: limoeiros têm folhas com um determinado formato, costumam atingir uma altura determinada e produzem flores e frutos específicos. Finalmente, com a referência a um limoeiro que está em determinado quintal, pode-se obter um entendimento mais preciso ainda, porém o alcance estará restrito a um único objeto.

7. Os termos podem ser divididos por: gênero, espécie e indivíduo. O indivíduo contém as características do gênero e da espécie, e é somente a partir desses termos universais que o conhecimento ou a ciência será possível. A ciência aborda os aspectos necessários e universais das coisas, e não os particulares. O que existe de universal e necessário no limoeiro “do meu quintal” é que ele produz limões como todos os outros, e não o fato de estar no meu quintal ou de um de seus galhos estar quebrado.

8. Doutrina do silogismo O desenvolvimento da ciência, isto é, do conhecimento daquilo que é universal e necessário nas coisas, implica o conhecimento das causas que tornam as afirmações possíveis. Para isso, Aristóteles desenvolveu a doutrina do silogismo, enquanto uma forma de raciocínio que, partindo de uma premissa, chega necessariamente a determinadas conclusões. Observe as seguintes proposições:

9. Todo homem é mortal. Sócrates é homem. As duas proposições anteriores resultam numa conclusão lógica: Logo, Sócrates é mortal.

10. Em outras palavras, a partir de duas premissas, chega-se a uma conclusão. No exemplo visto, “homem”, “mortal” e “Sócrates” são os três termos, sendo que “homem” é o termo médio, ou seja, aquele que fornece a razão do que foi afirmado: Sócrates é mortal porque é homem. Tal conclusão é rigorosa e nos dá uma certeza. Na Matemática, tradicionalmente usamos o procedimento da dedução, que funciona de acordo com os mesmos princípios: se x = y e y = z, então, infere-se que x = z.

11. A dedução se diferencia da indução. Nesta, o conhecimento é obtido por meio da análise de casos individuais que se repetem. A indução é a forma de obtenção de conhecimento científico por excelência, uma vez que é a partir dos diversos fenômenos que se repetem na natureza que se chega às leis do seu funcionamento. Finalmente, a analogia é uma forma de indução que parte de uma comparação.

12. Dedução – parte de uma lei universal e a aplica a casos particulares. Exemplos: • Todos os homens são falíveis. Einstein é um homem. Logo, Einstein é falível. • Todo número par é divisível por dois. 280 é um número par. Portanto, 280 é divisível por dois. • O conjunto dos números naturais está contido no conjunto dos números reais. 25 é um número natural. Logo, 25 é um número real.

13. Indução – parte de informações particulares e busca uma lei geral, universal. Exemplo: • O ferro conduz eletricidade. O ouro conduz eletricidade. O cobre conduz eletricidade. Logo, todos os metais conduzem eletricidade.

14. Analogia – tem uma forma de expressão própria que segue o modelo: A está para B, assim como C está para D. Por exemplo, diz-se que: “Os patins estão para o patinador, assim como os esquis estão para o esquiador”. Ou seja, a relação que os patins estabelecem com o patinador é idêntica à relação que os esquis estabelecem com o esquiador.

15. O silogismo não produz um novo conhecimento, mas organiza conhecimentos anteriores. Além disso, pode ser aplicado para a elaboração de proposições falsas, sem que isso altere sua perfeição formal. Exemplo: Todo homem é verde. Sócrates é homem. Logo, Sócrates é verde.

16. Esses falsos silogismos são chamados de sofismas (ou falácias) e, segundo Aristóteles, eram utilizados pelos sofistas para provar os argumentos mais descabidos. Por isso, para que sejam considerados científicos, os silogismos devem partir de premissas verdadeiras. A ciência, por sua vez, deve se fundar na realidade, indo além do mero raciocínio lógico coerente, que pode produzir armadilhas.

17. Falso dilema É dado um número limitado de opções (na maioria dos casos, apenas duas), quando de fato há mais. O falso dilema é um uso ilegítimo do operador “ou”. Exemplos: • Ou concordas comigo ou não. (Porque se pode concordar parcialmente.) • Reduz-te ao silêncio ou aceita o país que temos. (Porque uma pessoa tem o direito de denunciar o que entender.)

18. Apelo à ignorância Os argumentos desta classe concluem que algo é verdadeiro por não se ter provado que é falso; ou concluem que algo é falso porque não se provou que é verdadeiro. Esquece-se que a falta de prova não é uma prova. Exemplos: • Os fantasmas existem! Ou alguém já provou que não existem? • Como os cientistas não podem provar que vai ocorrer uma guerra global, ela provavelmente não ocorrerá.

19. Derrapagem Para mostrar que uma proposição P é inaceitável, extraem-se conseqüências inaceitáveis de P, e conseqüências das conseqüências. O argumento é falacioso quando pelo menos um dos seus passos é falso ou duvidoso. Mas a falsidade de uma ou mais premissas é ocultada pelos vários passos “se... então...”, que constituem o todo do argumento. Exemplo: • Se aprovarmos leis contra as armas de fogo, não demorará muito até aprovarmos leis contra todas as armas, e então começaremos a restringir todos os nossos direitos. Acabaremos por viver num estado totalitário. Portanto não devemos banir as armas automáticas.

20. Apelo à força É um argumento que tenta intimidar o ouvinte para garantir sua concordância com as idéias da afirmação. Exemplos: • Admita que a nova orientação da empresa é a melhor – se você pretende manter o emprego. • Faça assim ou você vai para o inferno quando morrer!

21. Reducionismo excessivo Consiste no erro de simplificar excessivamente idéias que fazem parte de contextos complexos e intelectualmente sofisticados, como os discursos científicos. Albert Einstein uma vez observou sobre os perigos de popularização de idéias científicas: “Se as explanações são fáceis demais, simples demais, o leitor pode ser enganado e acreditar que compreende algo quando de fato o autor deixou de delinear a verdadeira profundidade ou beleza de uma conquista científica”. Exemplo: • A idéia expressa por Darwin de que o homem é descendente do macaco é absolutamente inaceitável, pois a Bíblia diz que descendemos de Adão e Eva. (Explicação: Uma teoria, comprovada ou não, não pode ser reduzida ao fundamentalismo de uma religião.)

22. Generalização precipitada Afirma-se que o que é verdade em algumas instâncias deve ser verdade em todas ou em quase todas as instâncias, ou tenta-se estabelecer uma regra geral após achar algumas poucas evidências. Exemplo: • Entrevistei cem pessoas em duas favelas de São Paulo sobre seus hábitos alimentares. Acredito que as minhas conclusões são um retrato fiel dasituação alimentar da população carente da cidade.

23. Conhecimento não-demonstrativo Se o silogismo é um conhecimento demonstrativo, ele deve se basear em algum tipo de conhecimento evidente ou não-demonstrativo, que sirva para definir os termos. Existem três tipos de conhecimento não-demonstrativo: POSTULADOS DEFINIÇÃO AXIOMAS

24. • axiomas: verdades que não precisam de demonstrações. Exemplo: “Toda afirmação ou é verdadeira ou é falsa”. • postulados: ou pressupostos, entendidos como aquilo que deve ser admitido como ponto de partida para sustentar um sistema teórico. Exemplo: “Duas retas paralelas não se cruzam”. • definição: dividida em definição nominal (basicamente o nome do objeto) e definição real (indica a natureza do objeto). A partir da definição, a ciência chega ao conceito.

25. Para construir definições científicas baseadas na relação entre gêneros e espécies, seria necessário um levantamento em larga escala dos seres da natureza, bem como sua classificação. Grande parte da obra de Aristóteles estava voltada para essa finalidade.

26. http://www.defnarede.com/q.html

30. Resultado