1. O documento discute a hidrodinâmica e túneis de vento, explicando que túneis de vento tornam visíveis as linhas de fluxo do ar ao redor de objetos em movimento, permitindo avaliar a resistência do ar.
2. A hidrodinâmica teve origem na pré-história, mas foi formalizada por cientistas como Arquimedes, Leonardo da Vinci e Daniel Bernoulli. Túneis de vento permitem estudar aerodinâmica de forma similar.
3. A equação de continuidade est







![9
regiões das quais se conhece as áreas das seções nor-
mais. O uso do tubo em U para fazer a medida dessa di-
ferença, da forma como está representado na figura an-
terior, só é possível em tubos com gás. Com líquidos,
utilizam-se manômetros, instrumentos de medida dire-
ta da pressão que não são afetados pela passagem do
líquido. Podem-se usar manômetros localizados em di-
ferentes setores da tubulação (figura a seguir) ou manô-
metros para medir a diferença de pressão entre dois pon-
tos nos quais as áreas das seções normais são conhecidas
(foto abaixo).
b) Para S1 = 2,0 ؒ 10–2
m2
:
Φ = vS ⇒ Φ = v1S1 ⇒ 2,8 ؒ 10–2
= v1 ؒ 2,0 ؒ 10–2
⇒ v1 = 1,4 m/s
Para S2 = 5,00 ؒ 10–3
m2
:
Φ = vS ⇒ Φ = v2S2 ⇒ 2,8 ؒ 10–2
= v2 ؒ 5,0 ؒ 10–3
⇒ v2 = 5,6 m/s
Observação: O tubo de Ven-
turi é muito usado como va-
porizador. Veja a figura ao la-
do: a velocidade do ar sopra-
do no tubo horizontal torna a
pressão na extremidade supe-
rior do tubo vertical menor
do que a pressão atmosférica,
por isso o líquido contido no
recipiente sobe e, atingido pelo fluxo de ar, fragmenta-se em
gotículas.
Daí esse dispositivo ser chamado também de atomizador.
Muitos frascos de perfume, como o mostrado na foto a seguir,
funcionam dessa maneira.
x
y
Exercício resolvido
4 Suponha que o manômetro do tubo de Venturi mostrado na
foto anterior, instalado em uma canalização de água, meça a
diferença de pressão Δp = 1,5 ؒ 104
Pa. As áreas das seções nor-
mais desse tubo, correspondentes às pressões p1 (ramo
esquerdo do manômetro) e p2 (ramo direito do manômetro),
são, respectivamente, S1 = 2,0 ؒ 10–2
m2
e S2 = 5,0 ؒ 10–3
m2
.
Sendo dágua = 1,0 ؒ 103
kg/m3
e adotando g = 10 m/s2
, determine:
a) a vazão (Φ) da água;
b) os módulos v1 e v2 da velocidade do fluido ao passar por
S1 e S2.
Solução
a) Sendo Δp = p1 – p2 = 1,5 ؒ 104
Pa, da expressão do tubo de
Venturi:
Φ = S1S2
Ί
හහහහ
⇒
Φ = 1,0 ؒ 10–4
ؒ 2,8 ؒ 102
⇒ Φ = 2,8 ؒ 10–2
m3
/s ⇒ Φ = 28 L/s
Φ = ⋅ ⋅ ⋅
⋅ ⋅
⋅ ( ⋅ ) − ⋅
− −
− −
2,0 5,0
1,5
1,0 2,0 5,0
10 10
2 10
10 10 10
2 3
4
3 2 2 3[ ( )22]
⇒
2(p1 – p2)
d(S2
1 – S2
2)
B
A
Um atomizador bá-
sico se compõe ape-
nas de dois tubos em
ângulo reto e assim
pode ser encontrado
em lojas de produtos
para artistas. Veja as
imagens.
Atomizador básico.
A artista imerge o tubo maior do atomizador na tinta e sopra no bocal
do tubo horizontal para aspergi-la na tela. Podemos controlar a quan-
tidade de tinta variando a vazão e a velocidade do ar soprado.
EDUARDOSANTALIESTRA
www.french-home.com
EDUARDOSANTALIESTRA
EDUARDOSANTALIESTRA](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-9-320.jpg)


![12
fluidos tem de variar no interior dos tubos, o que,
em escoamentos laminares, ocorre como a figura
abaixo mostra.
Uma antiga reivindicação francesa pretende
dar ao Pa ؒ s o nome poiseuille, com o símbolo Pl,
para homenagear Jean Poiseuille. No entanto, até
hoje ela não foi acolhida.
velocidade
nula
velocidade
máxima
Variação da velocidade no interior de um fluido laminar em um
tubo: a curva em azul é o lugar geométrico da extremidade dos
vetores velocidade.
Por isso, quando nos referimos à velocidade
v= de um fluido no interior de um tubo, estamos
considerando como tal o vetor cujo módulo é a
média dos módulos das velocidades no interior
do fluido.
O módulo v da velocidade em um ponto P de
um fluido em escoamento laminar pode ser obtido
aproximadamente pela expressão a seguir, em que
r é o raio do tubo, d a distância do ponto ao eixo
desse tubo e C uma constante que depende do
tubo:
v = C(r2
– d2
)
Essa expressão é conhecida como Lei de
Poiseuille, pois foi estabelecida por Jean Poiseuille.
UNIDADE DE VISCOSIDADE
A unidade de viscosidade do SI pode ser obti-
da da sua definição. Se o módulo da força (F) é
medido em newtons (N), a distância (y) em metros
(m), a área (S) em metros quadrados (m2
), a veloci-
dade (v) em metros por segundo (m/s) e a pressão
em pascal [Pa = ], temos:
η = ⇒ η = ⇒
η = 5 6 ⇒ η = [Pa ؒ s]
Há uma antiga unidade prática ainda em uso,
denominada poise, cujos símbolos podem ser P, Ps
ou Po. A relação entre ela e Pa ؒ s é:
1 poise = 0,1 Pa ؒ s
N ؒ s
m2
[N ؒ m]
5m2
ؒ
m
6
s
Fy
Sv
N
m2
Atrito e viscosidade são fenômenos análogos e de
mesma origem, mas com características diferentes, que
podem ser delimitadas com clareza pela análise de ca-
racterísticas que diferenciam seus coeficientes.
O coeficiente de atrito é um número puro (adi-
mensional), depende do par de materiais em contato,
não caracteriza nenhuma substância e varia pouco com
a temperatura. O coeficiente de viscosidade tem unida-
de, caracteriza determinado fluido e varia drasticamen-
te com a temperatura. Veja o gráfico a seguir.
0 20
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,0
40 60 80 100
(и 10–3
Pa и s)
t (°C)
Se um fluido é arrastado por uma lâmina rígida,
como na figura a seguir, podemos concluir que a lâmi-
na e a película fluida nela aderida exercem sobre o res-
tante do fluido uma força resultante F=. Pelo Princípio
da Ação e Reação aparece na placa uma força de resis-
tência viscosa –F= aplicada pelo restante do fluido à placa
em movimento.
Gráfico coeficiente de viscosidade da água versus temperatura.
v=
F=–F=
Da definição do coeficiente de viscosidade pode-
mos expressar o módulo de F= assim:
F = ؒ v
S
y](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-12-320.jpg)

![14
junto em movimento retilíneo uniforme. Não levamos em
conta o trecho inicial porque nele a aceleração é variável e
no nível deste estudo não temos recursos de cálculo para
examinar essa situação. Além disso, a definição de viscosi-
dade e a expressão da força viscosa só podem ser aplicadas
em movimentos retilíneos com velocidade constante.
II. Note que não nos referimos ao atrito entre a placa e o líqui-
do, pois não existe atrito entre uma superfície rígida e um
fluido. A tração é exercida na placa rígida, mas a força de
reação viscosa do fluido é exercida na placa por intermé-
dio da película de fluido que a reveste e com ela se move
solidariamente.
III. Essa é uma situação experimental muito difícil de realizar,
principalmente pela impossibilidade de manter uniforme
a espessura da película de óleo. Por isso, apesar de seu for-
mato, este é um exercício teórico. Uma situação experi-
mental de fácil realização é apresentada no exercício
resolvido a seguir.
6 Uma esfera maciça de aço de 1,0 mm de raio cai verticalmen-
te com velocidade constante dentro de um tubo largo com óleo.
Verifica-se que ela desce 30 cm em 10 s. Dadas a densidade do
aço, daço = 7 800 kg/m3
, e a do óleo, dóleo = 800 kg/m3
, determi-
ne o coeficiente de viscosidade do óleo. Admita g = 10 m/s2
.
Solução
Na figura a seguir estão representadas as forças que atuam
sobre a esfera: o peso P=, o empuxo E= exercido pelo óleo sobre
a esfera e a força F= de resistência viscosa do óleo:
Sendo Vesfera = ؒ πr3
, r = 1,0 mm = 1,0 ؒ 10–3
m, uti-
lizando π = 3,1, temos:
Vesfera = ؒ 3,1(1,0 ؒ 10–3
)3
⇒ Vesfera = 4,1 ؒ 10–9
m3
Substituindo o valor de Vesfera em IV, obtemos o módulo F
da força de resistência viscosa:
F = (7 800 – 800)4,1 ؒ 10–9
ؒ 10 ⇒ F = 2,9 ؒ 10–4
N (V)
Para determinar o coeficiente de viscosidade do óleo apli-
cando a Lei de Stokes, precisamos saber qual é a velocida-
de de queda da esfera. Como ela é constante, Δx = 30 cm
= 0,30 m e Δt = 10 s:
v = ⇒ v = ⇒ v = 0,030 m/s
Então:
F = 6πηrv ⇒ 2,9 ؒ 10–4
= 6 ؒ 3,1η ؒ 1,0 ؒ 10–3
ؒ 0,030 ⇒
η = 0,52 Pa ؒ s
Observações:
I. Este exercício descreve uma atividade experimental relati-
vamente simples para determinar a viscosidade de um
líquido. A validade dessa determinação pode ser verifica-
da comparando o resultado obtido com valores tabelados
(veja a tabela da página 11). Para analisar corretamente os
resultados, três fatores devem ser considerados: a) os es-
treitos limites de validade da Lei de Stokes; por isso devem
ser utilizados líquidos de alto coeficiente de viscosidade
para que a queda da esfera ocorra a baixa velocidade (não
encontramos esses dados em relação à velocidade-limite
no óleo; estamos admitindo que o valor obtido aqui é viá-
vel por analogia ao da água); b) a largura do tubo deve ser
bem maior que o diâmetro da esfera; se o tubo for estrei-
to, as suas paredes vão interferir na resistência viscosa do
líquido, o que pode causar turbilhonamento e invalidar os
resultados; c) a temperatura do líquido deve ser anotada,
pois, como mostra o gráfico da página 12, o coeficiente de
viscosidade de um líquido varia significativamente com a
temperatura.
II. Quando a velocidade é nula, a força de resistência viscosa
também é nula; por isso o movimento de queda é acelera-
do no início e, à medida que a velocidade aumenta, a força
de resistência viscosa também aumenta, até que a resultan-
te das forças sobre a esfera se anule e o movimento passe a
ser retilíneo uniforme — essa é a velocidade-limite. Por essa
razão, as medidas das distâncias e dos tempos correspon-
dentes para a obtenção da velocidade da esfera só devem
ser feitas depois que ela já caiu por alguns segundos.
III. Assim como se pode determinar a viscosidade de um flui-
do conhecendo a velocidade-limite do corpo que o atraves-
sa, é possível determinar a velocidade-limite de um corpo
movendo-se através de um fluido conhecendo o coeficien-
te de viscosidade desse fluido. Foi a partir daí que o físico
experimental norte-americano Robert Millikan (1868-
-1953) pôde, em 1909, determinar a carga elétrica elemen-
tar e ganhar o prêmio Nobel de Física de 1923. O exercício
resolvido a seguir mostra uma etapa dessa experiência.
0,30
10
Δx
Δt
4
3
4
3
F=
P=
E=
Como a velocidade é constante, da Segunda Lei de Newton
em módulo, podemos escrever:
F + E = P ⇒ F = P – E (I)
Da definição de densidade [d = ], m = dV. Sendo P = mg,
o peso da esfera de aço pode ser expresso por:
P = daçoVesferag (II)
Da expressão do empuxo (E = dfluidoVfluido deslocadog), da
Hidrostática, podemos escrever:
E = dóleoVesferag (III)
Substituindo III e II em I:
F = daçoVesferag – dóleoVesferag ⇒ F = (daço – dóleo)Vesferag (IV)
m
V](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-14-320.jpg)
![15
7 Uma gota microscópica de óleo, de raio rgota = 4,0 μm, é aban-
donada no interior de uma câmara onde o ar está em repouso.
Sabendo que esse óleo tem densidade dóleo = 800 kg/m3
e que o
coeficiente de viscosidade do ar é ηar = 1,8 ؒ 10–5
Pa ؒ s, deter-
mine a velocidade-limite atingida por essa gota. Despreze o
empuxo do ar e admita g = 10 m/s2
.
Solução
Se o ar está em repouso e o empuxo por ele exerci-
do sobre a gota é desprezível, podemos afirmar que
sobre ela atuam duas forças: o seu peso P= e a força
de resistência viscosa F= exercida pelo ar.
Quando a velocidade-limite é atingida, essas duas
forças se equilibram, e a gota passa a cair com mo-
vimento retilíneo uniforme. Então, da Segunda Lei
de Newton em módulo, podemos escrever:
P – F = 0 ⇒ F = P (I)
Se a gota é esférica e não há turbulência, podemos aplicar a Lei
de Stokes:
F = 6πηarrgotav (II)
De I e II:
P = 6πηarrgotav ⇒ mgotag = 6πηarrgotav (III)
Da definição de densidade [d = ] e da expressão do
volume da esfera [V = ؒ πr3
], a massa da gota pode ser ex-
pressa na forma:
mgota = dóleoVgota ⇒ mgota = dóleo ؒ ؒ πr3
gota (IV)
Substituindo IV em III:
dóleo ؒ ؒ πr3
gotag = 6πηarrgotav ⇒ dóleo ؒ ؒ r2
gotag = 6ηarv
Sendo rgota = 4,0 μm = 4,0 ؒ 10–6
m e substituindo os demais
dados na expressão acima:
800 ؒ (4,0 ؒ 10–6
)2
10 = 6 ؒ 1,8 ؒ 10–5
v ⇒ v = 1,5 ؒ 10–2
m/s
Observações:
I. O valor obtido está dentro do limite para o movimento de
uma esfera sem turbulência no ar: v = 2 m/s. Se o resultado
ultrapassa esse valor, há turbulência e não podemos aplicar
a Lei de Stokes. Seria o caso de uma gota de óleo de 1,0 mm
de raio; obteríamos v = 100 m/s, valor que extrapola em
muito o limite de validade da Lei de Stokes para o ar.
II. Na experiência de Millikan borrifa-se óleo com um vapo-
rizador em uma câmara limitada por duas placas eletriza-
das e onde o ar está em repouso. Veja a figura a seguir.
4
3
4
3
4
3
4
3
4
3
m
V
Um orifício de entrada para a câmara seleciona as gotas de
raio compatível com os limites da Lei de Stokes. Eletri-
zadas por uma fonte externa ou na travessia do orifício, as
gotas são observadas por meio da ocular de um microscó-
pio. Escolhe-se uma gota de cada vez para análise. Por
recursos teóricos relativamente simples, mas ainda não
completamente estudados, determina-se a carga adquiri-
da por essa gota. A experiência é repetida dezenas ou cen-
tenas de vezes para outras tantas gotas. Obtêm-se, então,
dezenas ou centenas de valores da carga elétrica, mas
todos os valores obtidos são múltiplos de um mesmo va-
lor. Millikan concluiu que esse é o valor da carga elétrica
elementar — a carga do elétron —, menor carga elétrica
existente na natureza.
Para você resolver
5 A placa metálica plana representada na figura a
seguir tem área de 0,040 m2
e desliza sobre um
plano horizontal rígido apoiada em uma pelícu-
la de óleo de viscosidade η = 0,75 Pa ؒ s. Supõe-
-se que essa película seja contínua e uniforme e
tenha espessura y = 0,30 mm. O fio, inextensível
e de massa desprezível, é tracionado pelo bloco
B, de massa 60 g, e o atrito na roldana e a sua
massa são desprezíveis. Observa-se que o siste-
ma, ao ser posto em movimento, atinge rapida-
mente uma velocidade-limite. Qual é essa velo-
cidade? (Observação: Ao atingir a velocidade-
-limite, o sistema passa a se mover com veloci-
dade constante.) Adote g = 10 m/s2
.
P=
F=
(–)
ocular
placas
eletrizadas
orifício
raios X para
produzir carga
na gota de óleo
borrifo de pequenas
gotas de óleo
gota de óleo
carregada
sob análise
(+)
B
6 Uma esfera maciça de alumínio, de 2,0 mm de
raio, cai verticalmente em um tubo com gliceri-
na. Depois de atingir velocidade constante, veri-
fica-se que ela desce 18 cm em 20 s. Dadas a
densidade do alumínio, dAl = 2 700 kg/m3
, e a da
glicerina, dglicerina = 1300 kg/m3
, e admitindo
g = 10 m/s2
, determine:
a) a força de resistência viscosa exercida pela
glicerina;
b) o coeficiente de viscosidade da glicerina.
7 Sabendo que a velocidade-limite para a aplicação
da Lei de Stokes no ar é 2,0 m/s, qual deve ser o
valor limite do raio de uma gota de óleo para que
ela possa cair sem turbulência no ar em repouso?
(Dados: dóleo = 800 kg/m3
; ηar = 1,8 ؒ 10–5
Pa ؒ s;
g = 10 m/s2
; considere o empuxo do ar desprezível.)](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-15-320.jpg)



![20
Deduções
1a
) Equação de Continuidade
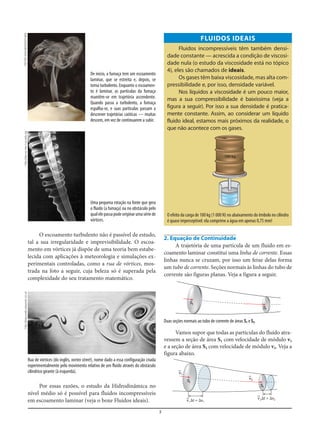
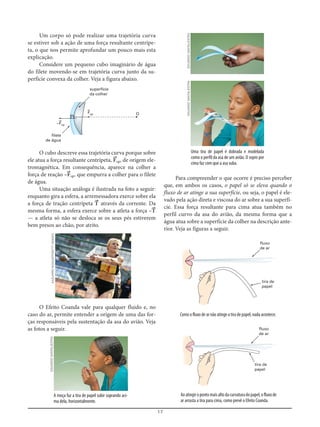
Reveja a última figura da página 3. Os trechos ha-
churados correspondem ao deslocamento de um fluido
ideal no mesmo intervalo de tempo ⌬t. Se o fluxo (Φ) é
constante e esse intervalo é suficientemente pequeno,
esses trechos podem ser considerados cilindros de áreas
S1 e S2. Nessas condições, vamos aplicar a esses dois
cilindros as definições de fluxo (Φ = vS) e de
velocidade média [v = ], nesse caso também cons-
tante, pois Φ e S são constantes. Para o cilindro de base S1:
Φ1 = ؒ S1
Como ⌬x1S1 = V1 (volume do cilindro de altura ⌬x1):
Φ1 = (I)
Por raciocínio análogo, para o cilindro de base S2:
Φ2 = (II)
Como Φ é constante e ⌬t é o mesmo, podemos
concluir de I e II que V1 = V2. Então, aplicando de novo
a expressão do volume do cilindro e lembrando que
⌬x = v⌬t:
V1 = V2 ⇒ S1⌬x1 = S2⌬x2 ⇒ S1v1⌬t = S2v2⌬t ⇒
S1v1 = S2v2 ou v1S1 = v2S2
2-a
) Equação de Bernoulli
Para esta dedução é preciso recordar as seguintes
expressões:
• densidade: d = e m = dV
• pressão: p = e F = pS (I)
• trabalho: τ = FΔx ؒ cos α (II)
• energia cinética: Ec = ؒ mv2
• energia potencial gravitacional: Epg = mg(h – h0)
Pela dedução anterior, sabemos que os dois cilin-
dros em cinza da primeira figura da página 5 têm o mes-
mo volume: V1 = V2. Como, tratando-se de um fluido
ideal, a densidade é constante, ambos têm a mesma mas-
sa m de fluido.
Ao deslocar-se pelo tubo do nível h1, com veloci-
dade de módulo v1, para o nível h2, com velocidade de
módulo v2, podemos afirmar que a massa de fluido con-
tida nesses cilindros sofre:
a) um acréscimo ΔEc de energia cinética:
ΔEc = ؒ m(v2
2
– v1
2
) ⇒ ΔEc = ؒ dV(v2
2
– v1
2
)
1
2
1
2
1
2
F
S
m
V
V2
⌬t
V1
⌬t
⌬x1
⌬t
⌬x
⌬t
Como V = V1 = Δx1S1 = v1ΔtS1 (ou V = V2 = v2ΔtS2):
ΔEc = ؒ dv1ΔtS1(v2
2
– v1
2
) (III)
b) um acréscimo ΔEp de energia potencial gravitacional:
ΔEp = mg(h2 – h1) ⇒ ΔEp = dv1ΔtS1g(h2 – h1) (IV)
Esses acréscimos de energia se devem ao trabalho
realizado por duas forças, uma decorrente da pressão
p1, de módulo F1 = p1S1, atuando em S1 no sentido do
movimento do fluido, e outra decorrente da pressão p2,
de módulo F2 = p2S2, atuando em S2 no sentido oposto.
Então, podemos escrever:
τF=1
+ τF=2
= ΔEc + ΔEp (V)
Da expressão da força em função da pressão e da
superfície (I), da definição de trabalho (II), lembrando que
em cada caso Δx = vΔt, e das expressões III e IV substituí-
das em V, temos:
p1S1v1Δt ؒ cos 0° + p2S2v2Δt ؒ cos 180° =
ؒ dv1ΔtS1(v2
2
– v1
2
) + dv1ΔtS1g(h2 – h1) ⇒
(p1 – p2)S1v1Δt = ؒ dv1ΔtS1(v2
2
– v1
2
) +
dv1ΔtS1g(h2 – h1) ⇒ p1 – p2 =
= ؒ d(v2
2
– v1
2
) + dg(h2 – h1)
3a
) Equação de Torricelli
Reveja a primeira figura da página 7. Vamos supor
que a área S do orifício seja muito menor que a área S0 da
superfície do tanque. Nesse caso, da Equação de Conti-
nuidade, podemos escrever:
v0S0 = vS ⇒ v0 = v ؒ
E concluir que v=0 também é muito menor que v=, ou
seja, que, em relação ao módulo de v=, podemos supor
v0 = 0.
Vamos admitir ainda que a pressão atmosférica, p0,
é a mesma na superfície do líquido e no orifício de saída
e que por ele o escoamento seja laminar. Nessas condi-
ções, aplicando a Equação de Bernoulli à superfície
(nível 1) e ao orifício (nível 2) e colocando o referencial
para as alturas no nível do orifício, temos:
p1 + ؒ dv1
2
+ dgh1 = p2 + ؒ dv2
2
+ dgh2 ⇒
p0 + ؒ dv0
2
+ dgh0 = p0 + ؒ dv2
+ dgh ⇒
p0 + ؒ d(0)2
+ dgh = p0 + ؒ dv2
+ dg(0) ⇒
dgh = ؒ dv2
⇒ v = Ίහහ2gh
1
2
1
2
1
2
1
2
1
2
1
2
1
2
S
S0
1
2
1
2
1
2
1
2](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-20-320.jpg)





![26
identificando como seus avanços foram modificando
as condições de vida e criando novas necessidades.
• Perceber o papel desempenhado pelo conhecimento
físico no desenvolvimento da tecnologia e a complexa
relação entre ciência e tecnologia ao longo da história.
Atividades interdisciplinares e de
contextualização
O assunto abordado aqui complementa os de
Hidrostática, que tratam dos líquidos em equilíbrio (os
gases em equilíbrio são objeto daTeoria Cinética dos Gases,
apresentada com o estudo da Termodinâmica).
Ter como temas principais a água, como líquido, e o ar,
como gás, possibilita a realização de inúmeras atividades
interdisciplinares e de contextualização. Esta pode ser tra-
balhada a partir da sua mais importante tecnologia — a
Aerodinâmica —, destacada na foto de abertura deste arti-
go. Além da sustentação de aviões e helicópteros, a
Aerodinâmica estuda a aderência dos veículos terrestres ao
solo e a redução da resistência do ar sobre eles. São assun-
tos que motivam extraordinariamente os adolescentes,
principalmente aqueles que gostam de corridas de auto-
móvel, área em que essa tecnologia é altamente desenvol-
vida — se o professor sugerir pesquisas nessa área, certa-
mente encontrará adesões entusiásticas.
O voo das aves e o movimento dos peixes, a forma
como esses animais se sustentam ou vencem a viscosidade
do ar ou da água e a função das penas nas aves e das esca-
mas nos peixes são também temas interessantíssimos que
podem proporcionar atividades interdisciplinares muito
motivadoras com a biologia.
Para você pensar
1. Por causa da aceleração da gravidade, a velocidade do
filete de água aumenta ao cair. Como a velocidade é in-
versamente proporcional à área da seção normal do tu-
bo de corrente, à medida que a velocidade aumenta
essa área diminui e o filete afina.
2. Em condições ideais, pelo Princípio da Conservação da
Energia, a água só pode atingir o mesmo nível da super-
fície. Portanto, mesmo nessas condições, a experiência
seria impossível. Na prática, como há perdas de energia
por causa da viscosidade da água e do ar, o esguicho fica
bem abaixo do nível da superfície.
3. a) Em I, sendo h1 = h2:
p1 + ؒ dv1
2
= p2 + ؒ dv2
2
⇒
p1 – p2 = ؒ dv2
2
– ؒ dv1
2
⇒ p1 – p2 = ؒ d(v2
2
– v1
2
)
Em II, como não há variação da seção normal
(S1 = S2 ⇒ v1 = v2):
1
2
1
2
1
2
1
2
1
2
p1 + dgh1 = p2 + dgh2 ⇒ p1 – p2 = dgh2 – dgh1 ⇒
p2 – p1 = dg(h2 – h1)
b) A diferença de pressões (p1 – p2) é responsável, em I,
só pela variação da energia cinética do líquido e, em
II, apenas pela variação da energia potencial gravita-
cional.
4. A afirmação é correta. Basta observar que a dedução da
expressão dessa lei (página 20) tem como ponto de par-
tida a identidade entre o trabalho realizado pelas forças
devidas às variações de pressão e as respectivas varia-
ções de energia cinética e potencial da água, conse-
quência do Princípio da Conservação da Energia Mecâ-
nica.
5. Como mostra a equação de Torricelli, a velocidade de saí-
da da água não depende da abertura do orifício, ou seja,
nesse caso apertar a saída da mangueirinha não aumenta
a velocidade de saída da água, o que invalida a ideia ini-
cial do aluno. Esse resultado não contraria a Equação de
Continuidade (v1S1 = v2S2), pois ela não se aplica a essa
situação porque a velocidade de abaixamento da super-
fície do recipiente foi considerada nula (desprezível).
Assim, cinematicamente, a altura máxima da água será
sempre igual à profundidade h do recipiente.
6. Não faz sentido falar em coeficiente de viscosidade está-
tico porque a viscosidade depende da existência do mo-
vimento relativo entre as diferentes camadas de um flui-
do. Não havendo esse movimento (v = 0), não existe vis-
cosidade e a expressão do coeficiente [η = ] perde o
seu significado.
7. A adesão viscosa do líquido ao bico do recipiente dirige
o líquido e o afina, tornando-o um filete laminar, o que
facilita o seu derramamento.
8. Ao cair através do ar, a curvatura da gota faz o fluxo de
ar curvar-se para contorná-la. Pelo Princípio da Ação e
Reação, a gota é puxada lateralmente para o fluxo e, por
isso, é ligeiramente achatada.
Para você resolver
1. a) Φ = ⇒ ΦE = ⇒ ΦE = 0,20 L/s ⇒
ΦE = 2,0 ؒ 10–4
m3
/s
b) rE = 0,50 cm = 5,0 ؒ 10–3
m ⇒ SE = πrE
2
⇒
SE = 3,1(5,0 ؒ 10–3
)2
⇒ SE = 7,8 ؒ 10–5
m2
ΦE = vESE ⇒ 2,0 ؒ 10–4
= vE ؒ 7,8 ؒ 10–5
⇒
vE = 2,6 m/s
c) rT = ⇒ rT = 1,3 cm = 1,3 ؒ 10–2
m ⇒
ST = πrT
2
⇒ ST = 3,1(1,3 ؒ 10–2
)2
⇒ ST = 5,2 ؒ 10–4
m2
2,5
2
12
60
V
Δt
Fy
Sv](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-26-320.jpg)
![27
5. Ao atingir a velocidade-limite, o sistema passa a se mo-
ver com velocidade constante. Logo, sendo mB = 0,060 kg
(reveja as figuras da bola na página 16):
T = PB ⇒ T = mBg ⇒ T = 0,060 ؒ 10 ⇒ T = 0,60 N
Esse é o módulo da força viscosa. Então, sendo
y = 0,30 mm = 3,0 ؒ 10–4
m, da expressão dessa força:
F = ؒ v ⇒ 0,60 = ؒ v ⇒
v = 6,0 ؒ 10–3
m/s
6. a) Reveja a figura da página 14. Como a velocidade é cons-
tante,daSegundaLeideNewtonemmódulo,podemos
escrever:
F + E = P ⇒ F = P – E ⇒
F = dAlVesferag – dglicerinaVesferag ⇒ F = (dAl – dglicerina)Vesferag
Vesfera = ؒ 3,1(2,0 ؒ 10–3
)3
⇒
Vesfera = 3,3 ؒ 10–8
m3
F = (2 700 – 1 300)3,3 ؒ 10–8
ؒ 10 ⇒ F = 4,6 ؒ 10–4
N
b) Sendo Δx = 18 cm = 0,18 m, Δt = 20 s e a velocidade
constante:
v = ⇒ v = ⇒ v = 9,0 ؒ 10–3
m/s
Então, da Lei de Stokes:
F = 6πηrv ⇒ 4,6 ؒ 10–4
=
6 ؒ 3,1η ؒ 2,0 ؒ 10–3
ؒ 9,0 ؒ 10–3
⇒ η = 1,4 Pa ؒ s
7. Reveja a primeira figura da página 15. Como a velocidade
é constante e o empuxo é desprezível, da Segunda Lei de
Newton em módulo podemos escrever:
P – F = 0 ⇒ F = P = mgotag (I)
Como a velocidade-limite é constante e a gota é esférica,
supondo não haver turbulência, podemos aplicar a Lei
de Stokes:
F = 6πηarrgotav (II)
De I e II:
mgotag = 6πηarrgotav (III)
Sendo d = e Vesfera = ؒ πr3
:
mgota = dóleoVgota ⇒ mgota = dóleo ؒ ؒ πr3
gota (IV)
Substituindo IV em III, sendo v = 2,0 m/s a velocidade-
-limite para o ar:
dóleo ؒ ؒ πr3
gotag = 6πηarrgotav ⇒
dóleo ؒ ؒ r2
gotag = 6ηarv ⇒
800 ؒ ؒ r2
gota ؒ 10 = 6 ؒ 1,8 ؒ 10–5
ؒ 2,0 ⇒
rgota = 1,4 ؒ 10–4
m
4
3
4
3
4
3
4
3
4
3
m
V
0,18
20
Δx
Δt
4
3
0,75ؒ0,040
3,0ؒ10–4
ηS
y
v1S1 = v2S2 ⇒ vESE = vTST ⇒
2,6 ؒ 7,8 ؒ 10–5
= vT ؒ 5,2 ؒ 10–4
⇒ vE = 0,39 m/s
2. a) Φ = 5,0 L/s = 5,0 ؒ 10–3
m3
/s
S1 = 1,2 ؒ 10–2
m2
⇒ Φ = v1S1 ⇒
5,0 ؒ 10–3
= v1 ؒ 1,2 ؒ 10–2
⇒ v1 = 0,42 m/s
S2 = 2,0 ؒ 10–3
m2
⇒ Φ = v2S2 ⇒
5,0 ؒ 10–3
= v2 ؒ 2,0 ؒ 10–3
⇒ v2 = 2,5 m/s
b) Fazendo p2 = p0 = 1,0 ؒ 105
Pa, da Equação de
Bernoulli:
p1 – p0 = ؒ d(v2
2
– v1
2
) + dg(h2 – h1) ⇒
p1 – 1,0 ؒ 105
= ؒ 1,0 ؒ 103
(2,52
– 0,422
) +
1,0 ؒ 103
ؒ 10(3,0 – 0) ⇒ p1 – 1,0 ؒ 105
=
3,1 ؒ 103
+ 3,0 ؒ 104
⇒ p1 = 1,3 ؒ 105
Pa
3. Da equação de Torricelli (v = ):
• para a profundidade hA = 0,080 m: vA = ⇒
vA = ⇒ vA = 1,3 m/s
• para hB = 0,16 m: vB = ⇒ vB = 1,8 m/s
• para hC = 0,24 m: vC = ⇒ vC = 2,2 m/s
Para um referencial em que a origem das alturas está fi-
xada no nível do solo, de acordo com a figura do item b,
exercício 3 da página 7:
• para as gotas que saem de A:
yA = 0,24 + 0,72 = 0,96 m
tempo de queda: y = y0 + v0yt + и gt2
⇒
0 = yA + 0 и tA + (–g)tA
2
⇒ 0 = 0,96 – 5,0tA
2
⇒
tA = 0,44 s
• para as gotas que saem de B:
yB = 0,16 + 0,72 = 0,88 m
0 = yB + 0 и tB + (–g)tB
2
⇒ 0 = 0,88 – 5,0tB
2
⇒
tB = 0,42 s
• para as gotas que saem de C:
yC = 0,080 + 0,72 = 0,90 m
0 = yC + 0 и tC + (–g)tC
2
⇒ 0 = 0,80 – 5,0tC
2
⇒
tC = 0,40 s
Portanto, os alcances serão:
• para as gotas que saem de A: x = x0 + vt ⇒
xA = x0 + vAtA ⇒ xA = 0 + 1,3 и 0,44 ⇒ xA = 0,57 m
• para as gotas que saem de B: xB = x0 + vBtB ⇒
xB = 0 + 1,8 и 0,42 ⇒ xB = 0,76 m
• para as gotas que saem de C: xC = x0 + vCtC ⇒
xC = 0 + 2,2 и 0,40 ⇒ xC = 0,88 m
4. Da expressão do tubo de Venturi:
Φ = S1S2Ί
හ හහහහ
⇒ p1 – p2 = ⇒
Δp = ⇒
Δp = 1,7 ؒ 103
Pa
(2,0ؒ10–2
)2
ؒ1,0 ؒ103
[(2,5ؒ10–2
)2
–(1,0ؒ10–2
)2
]
2(2,5 ؒ 10–2
ؒ 1,0 ؒ 10–2
)2
Φ2
d(S1
2
– S2
2
)
2(S1S2)2
2(p1 – p2)
d(S1
2
– S2
2
)
1
2
1
2
1
2
1
2
2 10⋅ ⋅0,24
2 10⋅ ⋅0,16
2 10⋅ ⋅0,080
2ghA
2gh
1
2
1
2](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-27-320.jpg)
![proporcional ao quadrado da sua velocidade – se ela
dobra (passa de 12 km/h a 24 km/h), a potência deve
tornar-se 4 (22
) vezes maior e passar de 6,0 kW para
24 kW (4 ؒ 6,0).
Resposta: alternativa a.
10. Como a massa específica da esfera é o dobro da massa
específica da água, podemos escrever
dágua = ؒ desfera. Então, pela expressão do empuxo
(E = dfluidoVfluido deslocadog), podemos determinar o empu-
xo dessa esfera inteiramente imersa na água:
Eesfera = dáguaVesferag ⇒ Eesfera = ؒ desferaVesferag ⇒
Eesfera = ؒ P
Como a velocidade é constante, a resultante sobre a
esfera é nula (reveja a figura da página 14). Da Segunda
Lei de Newton em módulo, sendo A a força viscosa:
A + Eesfera = P ⇒ A + ؒ P = P ⇒ P = 2A
Resposta: alternativa d.
11. Da Equação de Continuidade, sendo v1 = 1 m/s, onde
S1 = 500 m2
, obtemos S2, onde v2 = 2 m/s:
S1v1 = S2v2 ⇒ 500 ؒ 1 = S2 ؒ 2 ⇒ S2 = 250 m2
Resposta: alternativa a.
12. Até há pouco tempo esse fenômeno era associado à
Equação de Bernoulli (podemos afirmar que essa era a
resposta esperada pela banca). No entanto, a resposta
correta é o Efeito Coanda (curiosamente, essa mudança
de explicação foi divulgada pela primeira vez por físicos
da UFBA).
Supondo que o conjunto cartolina-prego seja sustenta-
do apenas pela diferença de pressão, o que não é mais
aceito como verdadeiro, a diferença de pressão média
mínima entre as faces da cartolina necessária para im-
pedir que o conjunto caia deve ser aquela que resulte
em uma força ascendente F= igual ao módulo P do peso
desse conjunto. Sendo m = 10 g = 1,0 и 10–2
kg a massa
do conjunto cartolina-prego e g = 10 m/s2
, o módulo da
força ascendente é:
F = P ⇒ F = mg ⇒ F = 1,0 и 10–2
и 10 ⇒ F = 0,10 N
Da definição de pressão, podemos escrever Δp = .
A área do disco de raio r = 2,0 cm = 2,0 ؒ 10–2
m é:
S = πr2
⇒ S = 3,1(2,0 ؒ 10–2
)2
= 1,2 ؒ 10–3
m2
Então:
Δp = ⇒ Δp = 83 Pa
0,10
1,2ؒ10–3
F
S
1
2
1
2
1
2
1
2
Preparação para o ingresso no ensino superior
1. Resposta: alternativa d.
2. Num escoamento laminar, a vazão é dada por Φ = vS.
Então, ela é diretamente proporcional à velocidade e à
área.
Resposta: alternativa d.
3. Da expressão dada podemos obter a dimensão de
C pela razão
5 6
. Portanto, a dimensão de C é 5 6 ou
m3
и s–1
.
Resposta: alternativa e.
4. Ainda dessa expressão, podemos determinar C usan-
do a expressão da velocidade do sangue (v = 0,28 m/s)
para um ponto P localizado no eixo central (d = 0) em
um vaso de raio r = 1,0 cm = 1,0 ؒ 10–2
m:
v = C(r2
– d2
) ⇒ 0,28 = C[(1,0 ؒ 10–2
)2
– 02
] ⇒
C = 2,8 ؒ 103
m3
ؒ s–1
Pela mesma expressão determinamos o valor de v para
d = 0,50 cm = 5,0 ؒ 10–3
m:
v = C(r2
– d2
) ⇒ v = 2,8 ؒ 103
[(1,0 ؒ 10–2
)2
–
(5,0 ؒ 10–3
)2
] ⇒ v = 0,21 m/s
Resposta: alternativa b.
5. Da Equação de Continuidade, chamando de A a área da
seção reta e sendo A2 = 3A1, podemos escrever:
A1v1 = A2v2 ⇒ A1v1 = 3A1v2 ⇒ v2 = [ ]v1
Logo, x = .
Resposta: alternativa d.
6. Da Equação de Continuidade, podemos concluir que, ao
passar de uma região de maior raio para outra de menor
raio, a velocidade da água aumenta. E, pela Equação de
Bernoulli, se a velocidade aumenta, a pressão diminui.
Resposta: alternativa c.
7. Chamando F de Fa, Fa + E = P (reveja o exercício resolvi-
do 6).
Resposta: alternativa c.
8. Resposta: alternativa c.
9. Da expressão da força viscosa (F = cv), lembrando a re-
lação entre a potência (P) e velocidade (v) de um mó-
vel em MRU (P = Fv), concluímos que P = cv2
. Logo, nas
condições dadas, a potência do barco é diretamente
1
3
1
3
m3
s
m
s
[m2
]
28](https://image.slidesharecdn.com/hidrodinamica-160316061713/85/Hidrodinamica-28-320.jpg)