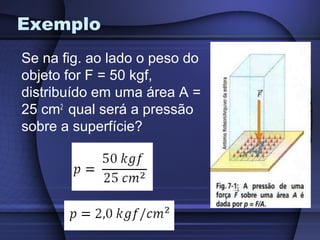
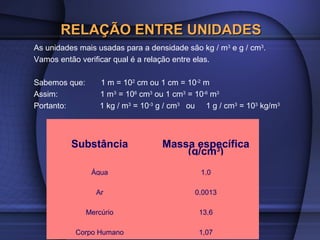
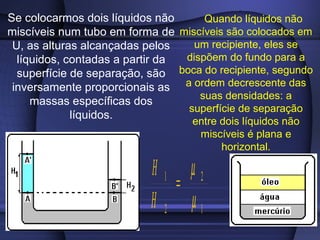
O documento discute conceitos fundamentais de hidrostática, incluindo: 1) A hidrostática estuda fluidos em repouso e pressão é definida como a força sobre uma área. 2) A pressão de um fluido varia com a profundidade e é igual ao produto da densidade, gravidade e altura. 3) A pressão atmosférica diminui com o aumento da altitude.

1. HIDROSTÁTICA
Daniela F. Almenara

2. Hidrostática
Hidrostática se refere ao
estudo dos fluídos em
repouso. Um fluído é
uma substância que
pode escoar facilmente
e que muda de forma
sob a ação de
pequenas
forças. Portanto fluido inclui os líquidos e
gases.

3. Conceito de pressão
Pressão p, da força F, sobre a área A, é a
relação entre o módulo de F e o valor da
área A, isto é:

4. Exemplo
Se na fig. ao lado o peso do
objeto for F = 50 kgf,
distribuído em uma área A =
25 cm2 qual será a pressão
sobre a superfície?

5. Comentários
O valor da pressão depende não só do
valor da força exercida, mas também da
área A na qual essa força está distribuída.
Uma vez fixado o valor de A, a pressão será
proporcional ao valor de F.
Por outro lado, uma mesma força poderá
produzir pressões diferentes, dependendo
da área sobre a qual ela atuar. Se a área for
muito pequena, poderemos obter grandes
pressões, mesmo com pequenas forças.

6. Por esse motivo, os objetos de corte (faca,
tesoura, enxada etc.) devem ser bem afiados e
os objetos de perfuração (prego, broca, etc),
pontiagudos. A área na qual atua a força exercida
por esses objetos será muito pequena,
acarretando uma grande pressão, o que torna
mais fácil o efeito desejado.

7. Densidade de um Corpo →d
m
p= m→massa do corpo(kg, g,...)
VCORPO VC →Volume do corpo(m3, cm3, L, ...)
Massa Específica de uma Substância → μ
m
µ= m→massa de subst.(kg, g,...)
VSUBST . VS →Volume de substância(m3, cm3, L)

8. ? DENSIDADE OU MASSA ESPECÍFICA ?
A diferença entre DENSIDADE e MASSA
ESPECÍFICA fica bem clara quando falamos
de objetos OCOS. Neste caso a DENSIDADE
leva em consideração o volume completo e a
MASSA ESPECÍFICA apenas a parte que
contêm substância
* *d ÁGUA = 1x10 kg / m = 1g / cm = 1kg / L
3 3 3
***Para líquidos e corpos maciços não há
distinção entre densidade e massa específica.

9. Exemplo
Um tambor cheio de gasolina tem a área da
base A = 0,75 m2 e a altura h = 2,0 m.
a) Qual é a massa de gasolina contida no
tambor

10. b) Qual é a pressão exercida, pela gasolina,
no fundo do tambor?

11. Exemplo: O corpo abaixo possui massa de 2.000 g.
Determine sua densidade e a massa específica do material
que o constitui.
m m
d= µ=
VCORPO VSUBST
2.000 2.000
d= µ=
500 400
400 cm3 100 cm3
d = 4 g / cm 3
µ = 5 g / cm 3

12. Atividades do livro, pág 237.
Exercícios: 1 ao 9

13. RELAÇÃO ENTRE UNIDADES
As unidades mais usadas para a densidade são kg / m3 e g / cm3.
Vamos então verificar qual é a relação entre elas.
Sabemos que: 1 m = 102 cm ou 1 cm = 10-2 m
Assim: 1 m3 = 106 cm3 ou 1 cm3 = 10-6 m3
Portanto: 1 kg / m3 = 10-3 g / cm3 ou 1 g / cm3 = 103 kg/m3
Substância Massa específica
(g/cm3)
Água 1,0
Ar 0,0013
Mercúrio 13,6
Corpo Humano 1,07

14. PRESSÃO
A pressão é a força a que um objeto está sujeito dividida
pela área da superfície sobre a qual a força age.
Definimos a força aqui como sendo uma força agindo
perpendicularmente à superfície.
PESO = (FORÇA)
FY
p=
A
ÁREA A
N N kgf
S .I . - u n id ( p ) = P a = 2
; 2 ; atm; cmHg
m cm
m²

15. Pressão Atmosférica
É a pressão que a atmosfera exerce sobre
a superfície da Terra.Varia de acordo com
a altitude e é possível medir o seu valor. Ao
nível do mar, ela é máxima e equivale a
uma coluna de 76 cmHg (= 1 atm).
N
1atm = 1,013 x10 2 = 76cmHg
5
m

16. Experiência de Torricelli
Torricelli,físico italiano,
realizou uma famosa
experiência que, além de
demonstrar que a pressão
existe realmente, permitiu a
determinação de seu valor.
Torricelli encheu de
mercúrio (Hg) um tubo de
vidro com mais ou menos 1
metro de comprimento;em
seguida fechou a extremidade
livre do tubo e o emborcou
numa vasilha contendo
mercúrio.
Quando a extremidade do px = p y
tudo foi aberta, a coluna de
mercúrio desceu, ficando o
seu nível aproximadamente 76 Mas px = patm e py = pcoluna,
cm acima do nível do mercúrio
dentro da vasilha. assim: patm = pcoluna

17. Pressão Hidrostática
É a pressão exercida por um líquido. Uma coluna de
líquido de densidade µ exerce pressão e que essa
pressão vale p = µ · g · h, sendo h a profundidade ou
a altura da coluna..
pH = µ.g .h
SI→ N/m2 kg/m3 m/s2 m
P h
h ↑⇒ p ↑
A

18. Variação da pressão exercida por um líquido
Pode-se demonstrar,de uma forma muito
simples, a variação de pressão com a
altura.Basta, para isso, fazermos
perfurações num recipiente cheio de
líquido em posições diferentes.O jorro sairá
cada vez mais forte à medida que
aumentarmos a altura da coluna de líquido
(isto é, nos pontos mais baixos).
Para dois líquidos
temos:
pH = μ1.g.h1 + μ2.g.h2

19. VALOR DA PRESSÃO ATMOSFÉRICA
Pascal repetiu a experiência no alto de uma montanha e
verificou que o valor da pressão atmosférica era menor
do que ao nível do mar. Concluiu que quanto maior for a
altitude do local, mais rarefeito será o ar e menor será a
altura da camada de ar que atuando na superfície de
mercúrio.
VARIAÇÃO DA PRESSÃO ATMOSFÉRICA COM A ALTITUDE
ALTITUDE (m) PRESSÃO ATMOSFÉRICA (cm Hg)
0 76 (10,33 mH2O)
500 72
1.000 67
2.000 60
3.000 53 (7,21 mH2O)

20. PRESSÃO TOTAL OU
ABSOLUTA
A pressão no interior de um líquido em
equilíbrio é a soma da pressão atmosférica e
da pressão da coluna de líquido. Patm
1
h
2
p = patm + µ · g · h
(PRESSÃO ABSOLUTA)

21. PRESSÕES ABSOLUTAS PRESSÕES RELATIVAS
p = patm + µ · g · h p= µ·g·h
p p
PRESSÕES
µ.g.h µ.g. POSITIVAS
patm patm 0 h
1 atm = 10,33 mH2O PRESSÕES
NEGATIVAS
0 -10,33 mH2O
(Vácuo absoluto) (Vácuo absoluto)

22. Teorema de Stevin
Os pontos 1 e 2 estão no interior de um fluido de densidade d.
pA = µ . g . hA
pB = µ . g . hB
Fazendo pB – pA, temos:
pB – pA = µ . g . hB – µ . g . hA
pB – pA = µ . g (hB – hA)
pB – pA = µ . g . ∆h
pA = pB + µ . g . ∆h
Δp = μ.g.Δh

23. PARADOXO HIDROSTÁTICO
Num fluido qualquer, a pressão não é a mesma em todos os
pontos. Porém, se um fluido homogêneo estiver em repouso,
então todos os pontos numa superfície plana horizontal estarão à
mesma pressão.
A pressão nas linhas marcadas na figura será a mesma,
se estiverem em um mesmo plano horizontal

24. Se colocarmos dois líquidos não Quando líquidos não
miscíveis num tubo em forma de miscíveis são colocados em
U, as alturas alcançadas pelos um recipiente, eles se
líquidos, contadas a partir da dispõem do fundo para a
superfície de separação, são boca do recipiente, segundo
inversamente proporcionais as a ordem decrescente das
suas densidades: a
massas específicas dos
superfície de separação
líquidos.
entre dois líquidos não
miscíveis é plana e
horizontal.
H1 µ2
=
H 2 µ1

25. Teorema de Pascal
A pressão aplicada a um fluido dentro de um recipiente
fechado é transmitida, sem variação, a todas as partes
do fluido, bem como às paredes do recipiente.
Aplicação:
Prensa Hidráulica
F1 F2
=
A1 A2

26. Princípio de Arquimedes
Todo corpo imerso total ou parcialmente num líquido recebe
uma força vertical, de baixo para cima, igual ao peso da
porção de líquido deslocada pelo corpo.
Empuxo
Força vertical de baixo para cima que o líquido exerce
sobre o corpo imerso.É o peso do liquido deslocado.
E = md .
Como, µ l g= m d md = µl .Vd,
Vd
substituímos: E = µl . Vd . g
A causa do empuxo é o fato de a pressão aumentar com a
profundidade!

27. HIDRODINÂMICA
A Hidrodinâmica é a parte da Física que estuda as
propriedades dos fluidos em movimento .
O nosso estudo da Hidrodinâmica no Ensino Médio determina
algumas condições iniciais: o fluido tratado aqui será sempre
ideal, ou seja, não-viscoso, homogêneo e velocidade de esco-
amento constante em um determinado ponto em relação ao
tempo(regime estacionário).

28. Escoamento rotacional ou turbulento. O escoamento
turbulento é um escoamento irregular, caracterizado por regiões
de pequenos vórtices.Como exemplo, o escoamento da água
numa corrente fica turbulento nas regiões onde as rochas, ou
outros obstáculos, estão no leito e contribuem para a formação
dos rápidos encachoeirados
O Escoamento se diz laminar ou estacionário se cada partícula do
fluido segue uma trajetória definida e suave, e se as trajetórias
das partículas não se cruzam.
No escoamento laminar, portanto, a velocidade do fluido, em cada
ponto,permanece constante com o tempo. Ex.: a água se
movendo num rio calmo , de leito regular e sem obstáculos.

29. ESCOAMENTO
ESTÁCIONÁRIO

30. Equação da continuidade
A1v1 = A2v2

31. EQUAÇÃO DE BERNOULLI
dv12 2
dv 2
P1 + dgh1 + = P2 + dgh2 +
2 2

32. SUSTENTAÇÃO DE AVIÕES
As asas são construídas de forma a que o ar se mova mais depressa na parte
de cima da asa, fazendo com que a pressão por cima da asa seja mais baixa

33. Aplicações da equação de
Bernoulli
• Teorema de Torricelli
v = 2 gh

34. Tubo de Venturi
• O Tubo de Venturi é um elemento medidor de vazão
de diferencial de pressão, também chamado de
medidor de vazão por obstrução de área. A diferença
de pressão entre duas seções distintas do medidor é
proporcional à vazão que escoa por ele
• Algumas das principais razões de usar elementos de
obstrução para se medir vazão são as seguintes:
• Podem ser usados para medir qualquer fluido.
• Não há nenhum elemento mecânico imerso no
escoamento.
• Não há limite de vazão a ser medida, ou seja, a
tubulação pode ter qualquer diâmetro

35. Tubo de Venturi

36. Tubo de Pitot
- O Tubo de Pitot no avião serve
para 2 Finalidades
- Marcar a velocidade relativa
( Ve ocimetro ) entre a aeronave e
o ar ( Chamado de Air Speed )
- Marcar a Altitude ou a Altura
( Altimetro ) com a qual a
aeronave está sobrevoando .
Em um carro de F1 o tubo de Pitot
controla a pressão do ar, e pode
diminuir, no caso de estar
erradamente colocado, em cerca
de 7 cavalos a potencia do motor
FIM DA AULA