O documento discute conceitos fundamentais de cálculo diferencial e integral, incluindo: (1) Definições de pontos de máximo e mínimo local e global de uma função; (2) Condição necessária para um ponto ser um extremo é ser um ponto crítico; (3) Teorema de que uma função contínua em um intervalo fechado atinge valores máximo e mínimo absolutos.

1. Cálculo Diferencial e Integral I
Universidade Federal do Recôncavo da Bahia
01/06/2022
Paulo Henrique Ribeiro do Nascimento

2. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Sejam f : D → R uma função e x0 ∈ D. Dizemos que x0 é ponto:
de máximo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≤ f(x0), ∀ x ∈ I;
de máximo global (ou absoluto): se f(x) ≤ f(x0), ∀ x ∈ D;
de mínimo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≥ f(x0), ∀ x ∈ I;
de mínimo global (ou absoluto): se f(x) ≥ f(x0), ∀ x ∈ D;
extremo: se x0 é ponto de máximo ou de mínimo;
crítico: se f′(x0) = 0 ou f′(x0) não existir.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

3. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Sejam f : D → R uma função e x0 ∈ D. Dizemos que x0 é ponto:
de máximo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≤ f(x0), ∀ x ∈ I;
de máximo global (ou absoluto): se f(x) ≤ f(x0), ∀ x ∈ D;
de mínimo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≥ f(x0), ∀ x ∈ I;
de mínimo global (ou absoluto): se f(x) ≥ f(x0), ∀ x ∈ D;
extremo: se x0 é ponto de máximo ou de mínimo;
crítico: se f′(x0) = 0 ou f′(x0) não existir.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

4. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Sejam f : D → R uma função e x0 ∈ D. Dizemos que x0 é ponto:
de máximo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≤ f(x0), ∀ x ∈ I;
de máximo global (ou absoluto): se f(x) ≤ f(x0), ∀ x ∈ D;
de mínimo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≥ f(x0), ∀ x ∈ I;
de mínimo global (ou absoluto): se f(x) ≥ f(x0), ∀ x ∈ D;
extremo: se x0 é ponto de máximo ou de mínimo;
crítico: se f′(x0) = 0 ou f′(x0) não existir.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

5. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Sejam f : D → R uma função e x0 ∈ D. Dizemos que x0 é ponto:
de máximo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≤ f(x0), ∀ x ∈ I;
de máximo global (ou absoluto): se f(x) ≤ f(x0), ∀ x ∈ D;
de mínimo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≥ f(x0), ∀ x ∈ I;
de mínimo global (ou absoluto): se f(x) ≥ f(x0), ∀ x ∈ D;
extremo: se x0 é ponto de máximo ou de mínimo;
crítico: se f′(x0) = 0 ou f′(x0) não existir.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

6. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Sejam f : D → R uma função e x0 ∈ D. Dizemos que x0 é ponto:
de máximo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≤ f(x0), ∀ x ∈ I;
de máximo global (ou absoluto): se f(x) ≤ f(x0), ∀ x ∈ D;
de mínimo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≥ f(x0), ∀ x ∈ I;
de mínimo global (ou absoluto): se f(x) ≥ f(x0), ∀ x ∈ D;
extremo: se x0 é ponto de máximo ou de mínimo;
crítico: se f′(x0) = 0 ou f′(x0) não existir.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

7. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Sejam f : D → R uma função e x0 ∈ D. Dizemos que x0 é ponto:
de máximo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≤ f(x0), ∀ x ∈ I;
de máximo global (ou absoluto): se f(x) ≤ f(x0), ∀ x ∈ D;
de mínimo local (ou relativo): se existe um intervalo aberto I contendo x0 tal
que f(x) ≥ f(x0), ∀ x ∈ I;
de mínimo global (ou absoluto): se f(x) ≥ f(x0), ∀ x ∈ D;
extremo: se x0 é ponto de máximo ou de mínimo;
crítico: se f′(x0) = 0 ou f′(x0) não existir.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

8. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
x
y
0 15
−15 a
b
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

9. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
x
y
0 15
−15 a
b
A figura acima mostra o esboço de parte do gráfico da função f(x) = x · sin(x), x ≤ 0
e f(x) = −x · sin(x), x > 0, que possui um valor mínimo local em b e um valor máximo
local em a. Observe que existem apenas extremos locais.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

10. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Um extremo absoluto de uma função num intervalo é um valor máximo absoluto ou
um mínimo absoluto da função no intervalo. Um função pode ou não ter um extremo
absoluto no intervalo dado. Vejamos os exemplos a seguir.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

11. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Um extremo absoluto de uma função num intervalo é um valor máximo absoluto ou
um mínimo absoluto da função no intervalo. Um função pode ou não ter um extremo
absoluto no intervalo dado. Vejamos os exemplos a seguir.
Example 1.
O gráfico da função f definida por f(x) = x2 − 4x é uma
parábola e o seu esboço está na figura ao lado. O ponto
mais baixo da parábola está em (2, 4) e a parábola possui a
parte côncava para cima. Nesse caso, a função tem um valor
mínimo absoluto de 4 em 2. Não há valor máximo absoluto
de f. Note que f′(2) = 0, ou seja, 2 é ponto crítico de f.
x
y
2
4
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

12. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
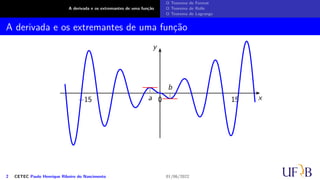
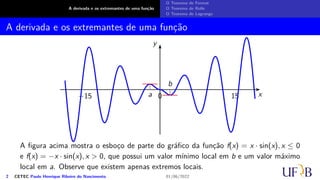
Um extremo absoluto de uma função num intervalo é um valor máximo absoluto ou
um mínimo absoluto da função no intervalo. Um função pode ou não ter um extremo
absoluto no intervalo dado. Vejamos os exemplos a seguir.
Example 1.
Seja f(x) = 2x definida em ]1, 4]. Um esboço do gráfico
está de f está na figura ao lado. Observe que não há valor
mínimo absoluto de f em (1, 4], no entanto f tem valor de
máximo absoluto igual a 8 em (1, 4].
x
y
1 4
2
8
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

13. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Example 1.
Seja f a função definida em [−5, 4] por
f(x) =
{
x , x < 1
x2 − 6x , x ≥ 1.
O valor máximo absoluto de f ocorre em x = 1 e
f(1) = 2; o valor mínimo absoluto de f ocorre em −5 e
f(−5) = −4. Note que f tem um valor máximo relativo
em 4 e que x = 1 é um número crítico de f, pois f′(1)
não existe e x = 3 é um número crítico de f, já que
f′(3) = 0.
x
y
(−5, −4)
(1, 2)
(3, −2)
(4, −1)
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

14. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Theorem 1 (do valor extremo ou de Weirstrass).
Se f : [a, b] → R é uma função contínua, então f assume valor máximo e mínimo
absoluto em [a, b].
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

15. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Theorem 1 (do valor extremo ou de Weirstrass).
Se f : [a, b] → R é uma função contínua, então f assume valor máximo e mínimo
absoluto em [a, b].
O valor extremo absoluto de uma função contínua definida em um intervalo fechado
sempre existirá, quer seja no intervalo (a, b) ou em x = a ou x = b.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

16. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Como uma condição necessária para que uma função tenha um extremo relativo em
x = c é que c seja um número crítico, o valor máximo absoluto e o valor mínimo
absoluto de uma função contínua f definida em um intervalo fechado [a, b] podem ser
determinados pelo seguinte procedimento:
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

17. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Como uma condição necessária para que uma função tenha um extremo relativo em
x = c é que c seja um número crítico, o valor máximo absoluto e o valor mínimo
absoluto de uma função contínua f definida em um intervalo fechado [a, b] podem ser
determinados pelo seguinte procedimento:
Ache os valores da função nos números críticos de f em (a, b);
Ache os valores de f(a) e f(b);
O maior valor dentre os valores obtidos das etapas anteriores será o valor máximo
absoluto e o menor, o valor mínimo absoluto.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

18. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Ache os valores da função nos números críticos de f em (a, b);
Ache os valores de f(a) e f(b);
O maior valor dentre os valores obtidos das etapas anteriores será o valor máximo
absoluto e o menor, o valor mínimo absoluto.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

19. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Ache os valores da função nos números críticos de f em (a, b);
Ache os valores de f(a) e f(b);
O maior valor dentre os valores obtidos das etapas anteriores será o valor máximo
absoluto e o menor, o valor mínimo absoluto.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

20. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Example 1.
Seja f(x) = x3 + x2 − x uma função definida em
[
−2,
1
2
]
(ver figura ao lado). x
y
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

21. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Example 1.
Seja f(x) = x3 + x2 − x uma função definida em
[
−2,
1
2
]
(ver figura ao lado).
Como a função é contínua, o teorema do valor
extremo pode ser aplicado para determinarmos as
coordenadas dos extremos absolutos. Para achar os
números críticos de f, resolveremos a equação
f′(x) = 3x2 + 2x − 1 = 0.
x
y
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

22. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Example 1.
Então f′(x) = 0 ⇔ x = −1 ou x = 1
3, são os
números críticos de f, e cada um deles pertence ao
intervalo fechado [−2, 1
2 ]. x
y
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

23. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Example 1.
Então f′(x) = 0 ⇔ x = −1 ou x = 1
3, são os
números críticos de f, e cada um deles pertence ao
intervalo fechado [−2, 1
2 ].
Os valores da função nos números críticos e nos
extremos do intervalo estão dados na tabela ao lado. O
valor máximo absoluto de f é portanto 2, o mínimo
absoluto é −1.
x
y
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

24. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
A derivada e os extremantes de uma função
Example 1.
x −2 −1 1
3
1
2
f(x) −1 2 22
27
7
8 x
y
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

25. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

26. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
O teorema de Fermat nos permite estabelecer quais são os possíveis extremantes de uma
função derivável.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

27. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
O teorema de Fermat nos permite estabelecer quais são os possíveis extremantes de uma
função derivável.
Theorem 2 (de Fermat).
Se f : D → R é uma função derivável num ponto de extremo local interior x0 ∈ D,
então f′(x0) = 0.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

28. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Theorem 2 (de Fermat).
Se f : D → R é uma função derivável num ponto de extremo local interior x0 ∈ D,
então f′(x0) = 0.
Demonstração: Se x0 é ponto de extremo local interior, então existe uma vizinhança
V de x0 tal que, ∀ x ∈ V,
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

29. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Theorem 2 (de Fermat).
Se f : D → R é uma função derivável num ponto de extremo local interior x0 ∈ D,
então f′(x0) = 0.
Demonstração: Se x0 é ponto de extremo local interior, então existe uma vizinhança
V de x0 tal que, ∀ x ∈ V,
f(x0) ≤ f(x) ⇒





f(x) − f(x0)
x − x0
≤ 0 , x < x0
f(x) − f(x0)
x − x0
≥ 0 , x > x0.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

30. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Como f é derivável em x0, temos que lim
x0
f(x) − f(x0)
x − x0
existe, é finito e é igual a f′(x0).
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

31. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Como f é derivável em x0, temos que lim
x0
f(x) − f(x0)
x − x0
existe, é finito e é igual a f′(x0).
Analisando os limites laterais lim
x−
0
f(x) − f(x0)
x − x0
= f′
(x0) ≤ 0 e lim
x0
f(x) − f(x0)
x − x0
= f′
(x0) ≥
0, podemos concluir que f′(x0) = 0. 2
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

32. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Theorem 2 (de Fermat).
Se f : D → R é uma função derivável num ponto de extremo local interior x0 ∈ D,
então f′(x0) = 0.
Observação: O recíproco do teorema de Fermat não é válido, ou seja, existem funções
deriváveis em um ponto x0 pertencente ao interior do domínio da f tal que f′(x0) = 0,
porém x0 não é ponto de extremo.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

33. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Example 2.
Dada a função f(x) = (x − 2)3, verifique se o ponto x0 = 2 é um possível ponto de
extremo de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

34. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Example 2.
Dada a função f(x) = (x − 2)3, verifique se o ponto x0 = 2 é um possível ponto de
extremo de f.
Solução: Observe que f′(2) = 0 e, portanto, é um possível extremante. Porém, ele não
é ponto de extremo para f. Basta observar o esboço do seu gráfico.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

35. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Fermat
Example 2.
Dada a função f(x) = (x − 2)3, verifique se o
ponto x0 = 2 é um possível ponto de extremo de f.
Solução: Observe que f′(2) = 0 e, portanto, é um
possível extremante. Porém, ele não é ponto de extremo
para f. Basta observar o esboço do seu gráfico.
x
y
2
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

36. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica do Teorema de Fermat
O teorema de Fermat nos garante que em um extremo local interior de uma função
derivável f, a reta tangente ao gráfico de f no ponto (x0, f(x0)) é paralela ao eixo das
abscissas.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

37. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

38. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
O teorema de Rolle nos dá a condição de existência de pelo menos um ponto que anula
a derivada de uma função em um intervalo.
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

39. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
O teorema de Rolle nos dá a condição de existência de pelo menos um ponto que anula
a derivada de uma função em um intervalo.
Theorem 3 (de Rolle).
Se f : [a, b] → R é uma função contínua em [a, b], derivável em ]a, b[ e
f(a) = f(b), então existe pelo menos um ponto x0 ∈]a, b[ tal que f′(x0) = 0.
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

40. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

41. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função constante em [a, b].
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

42. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função constante em [a, b].
• f é uma função não constante em [a, b].
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

43. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função constante em [a, b].
Neste caso, f′(x0) = 0, ∀ x0 ∈]a, b[.
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

44. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função não constante em [a, b].
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

45. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função não constante em [a, b].
Neste caso, existe x ∈]a, b[ tal que f(x) ̸= f(a) = f(b).
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

46. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função não constante em [a, b].
Neste caso, existe x ∈]a, b[ tal que f(x) ̸= f(a) = f(b).
Como f é contínua em [a, b], f possui pelo menos um extremo em [a, b].
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

47. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função não constante em [a, b].
Neste caso, existe x ∈]a, b[ tal que f(x) ̸= f(a) = f(b).
Como f é contínua em [a, b], f possui pelo menos um extremo em [a, b].
Se existe x ∈]a, b[ tal que f(x) > f(a) = f(b), então a e b não são pontos de máximo de
f.
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

48. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função não constante em [a, b].
Neste caso, existe x ∈]a, b[ tal que f(x) ̸= f(a) = f(b).
Como f é contínua em [a, b], f possui pelo menos um extremo em [a, b].
Se existe x ∈]a, b[ tal que f(x) > f(a) = f(b), então a e b não são pontos de máximo de
f.
Portanto, f assumirá valor máximo em algum ponto x0 ∈]a, b[ e, sendo f derivável em
]a, b[, temos f′(x0) = 0 (Teorema de Fermat).
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

49. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Rolle
Demonstração: Analisemos os seguintes casos:
• f é uma função não constante em [a, b].
Neste caso, existe x ∈]a, b[ tal que f(x) ̸= f(a) = f(b).
Como f é contínua em [a, b], f possui pelo menos um extremo em [a, b].
Se existe x ∈]a, b[ tal que f(x) > f(a) = f(b), então a e b não são pontos de máximo de
f.
Portanto, f assumirá valor máximo em algum ponto x0 ∈]a, b[ e, sendo f derivável em
]a, b[, temos f′(x0) = 0 (Teorema de Fermat).
Se existe x ∈]a, b[ tal que f(x) < f(a) = f(b), o argumento é análogo.
2
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

50. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica para o Teorema de Rolle
6 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

51. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica para o Teorema de Rolle
A figura ao lado mostra um esboço do gráfico de uma
função f que satisfaz as condições do teorema. Vemos
intuitivamente que existe pelo menos um ponto sobre so-
bre a curva entre os pontos (a, f(a)) e (b, f(b)), onde a
reta tangente é paralela ao eixo x, por exemplo o ponto
de abscissa c, ou seja, f′(c) = 0.
6 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

52. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica para o Teorema de Rolle
A figura ao lado mostra um esboço do gráfico de uma
função f que satisfaz as condições do teorema. Vemos
intuitivamente que existe pelo menos um ponto sobre so-
bre a curva entre os pontos (a, f(a)) e (b, f(b)), onde a
reta tangente é paralela ao eixo x, por exemplo o ponto
de abscissa c, ou seja, f′(c) = 0.
x
y
a b
c d
6 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

53. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Atividades
Exercício 1.1.
Verifique se estão satisfeitas as hipóteses do Teorema de Rolle para as funções a
seguir, nos intervalos especificados.
a) f(x) = 4x3 − 9x2, I1 = [0, 1], I2 =
[
1,
5
2
]
e I3 =
[
0,
5
2
]
;
b) f(x) =
2x2 − 3x
3x − 4
e I =
[
1
2
, 1
]
;
c) f(x) =
{
x , x ≤ 2
4 − x , x > 1
e I = [−2, 4].
7 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

54. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

55. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
Theorem 3 (de Lagrange ou do valor médio).
Se f : [a, b] → R é uma função contínua em [a, b] e derivável em (a, b), então
existe pelo menos um ponto x0 ∈ (a, b) tal que
f(b) − f(a)
b − a
= f′
(x0).
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

56. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
Demonstração: Analisemos os seguintes casos:
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

57. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
Demonstração: Analisemos os seguintes casos:
f(a) = f(b).
f(a) ̸= f(b).
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

58. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
f(a) = f(b).
f(a) ̸= f(b).
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

59. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
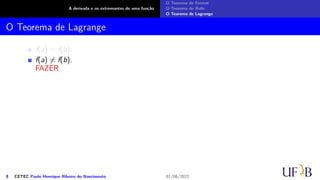
f(a) = f(b).
Neste caso,
f(b) − f(a)
b − a
= 0 e, pelo teorema de Rolle, existe x0 ∈]a, b[ tal que
f′(x0) = 0.
f(a) ̸= f(b).
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

60. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
f(a) = f(b).
f(a) ̸= f(b).
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

61. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
O Teorema de Lagrange
f(a) = f(b).
f(a) ̸= f(b).
FAZER
8 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

62. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
9 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

63. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Num esboço do gráfico da função f,
f(b) − f(a)
b − a
é a inclinação
do segmento de reta que liga os pontos A(a, f(a)) e B(b, f(b)).
O teorema do valor médio afirma que existe um ponto sobre
a curva entre A e B, onde a reta tangente é paralela à reta
secante por A e B, ou seja, existe um c ∈ (a, b) tal que
f′(c) =
f(b) − f(a)
b − a
.
9 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

64. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Num esboço do gráfico da função f,
f(b) − f(a)
b − a
é a inclinação
do segmento de reta que liga os pontos A(a, f(a)) e B(b, f(b)).
O teorema do valor médio afirma que existe um ponto sobre
a curva entre A e B, onde a reta tangente é paralela à reta
secante por A e B, ou seja, existe um c ∈ (a, b) tal que
f′(c) =
f(b) − f(a)
b − a
.
x
y
A
B
a b
c
9 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

65. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Num esboço do gráfico da função f,
f(b) − f(a)
b − a
é a inclinação
do segmento de reta que liga os pontos A(a, f(a)) e B(b, f(b)).
O teorema do valor médio afirma que existe um ponto sobre
a curva entre A e B, onde a reta tangente é paralela à reta
secante por A e B, ou seja, existe um c ∈ (a, b) tal que
f′(c) =
f(b) − f(a)
b − a
.
x
y
A
B
a b
c
Se tomarmos a reta secante AB paralela ao eixo x, podemos observar que o teorema do
valor médio é uma generalização do teorema de Rolle.
9 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

66. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Teorema
Theorem 3.
Se f for uma função tal que f′(x) = 0, para todos os valores de x num intervalo I,
então f é constante.
Demonstração: FAZER
10 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

67. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios de determinação de intervalos monótonos
Podemos estabelecer alguns critérios que nos ajudarão a determinar o conjunto dos
valores de x os quais uma função é crescente ou decrescente.
Theorem 4.
Se f : [a, b] → R é uma função contínua em [a, b] e derivável em (a, b), então:
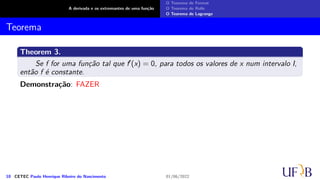
1 f′(x) > 0, ∀ x ∈ [a, b] ⇔ f(x2) > f(x1), x2 > x1 (f é crescente em [a, b]);
2 f′(x) < 0, ∀ x ∈ [a, b] ⇔ f(x2) < f(x1), x2 > x1 (f é decrescente em [a, b]).
Demonstração: FAZER
11 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

68. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
12 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

69. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Seja f uma função derivável. Afirmar que f é crescente (decrescente) em ]a, b[ equivale
a afirmar que f′(x) ≥ 0, ∀ x ∈]a, b[ (f′(x) ≤ 0, ∀ x ∈]a, b[), ou seja, os coeficientes
angulares das retas tangentes ao gráfico de f são não negativos (não positivos).
12 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

70. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Seja f uma função derivável. Afirmar que f é crescente (decrescente) em ]a, b[ equivale
a afirmar que f′(x) ≥ 0, ∀ x ∈]a, b[ (f′(x) ≤ 0, ∀ x ∈]a, b[), ou seja, os coeficien-
tes angulares das retas tangentes ao gráfico de f são não negativos (não positivos).
Observe na figura ao lado, que quando a inclinação da reta
tangente for positiva, a função será crescente e quando a
inclinação da reta for negativa, a função será decrescente.
Como f′(x) é a inclinação da reta tangente à curva y =
f(x), f é crescente quando f′(x) > 0 e decrescente quando
f′(x) < 0.
12 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

71. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Seja f uma função derivável. Afirmar que f é crescente (decrescente) em ]a, b[ equivale
a afirmar que f′(x) ≥ 0, ∀ x ∈]a, b[ (f′(x) ≤ 0, ∀ x ∈]a, b[), ou seja, os coeficien-
tes angulares das retas tangentes ao gráfico de f são não negativos (não positivos).
Observe na figura ao lado, que quando a inclinação da reta
tangente for positiva, a função será crescente e quando a
inclinação da reta for negativa, a função será decrescente.
Como f′(x) é a inclinação da reta tangente à curva y =
f(x), f é crescente quando f′(x) > 0 e decrescente quando
f′(x) < 0.
12 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

72. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Exemplo
Example 5.
A função f(x) = 2 é constante. Sua derivada é f′(x) = 0, ∀x ∈ R;
A função f(x) = x3 é crescente em R pois sua derivada é f′(x) = 3x2 ≥ 0, ∀x ∈ R;
A função f(x) =
1
x
é decrescente em qualquer intervalo que não contenha o zero,
pois sua derivada é f′(x) = −
1
x2
< 0, ∀x ∈ R∗.
13 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

73. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios para a Determinação de Extremantes de uma Função Derivável
14 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

74. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios para a Determinação de Extremantes de uma Função Derivável
O teorema de Fermat nos garante que, se f é uma função definida em [a, b] e derivável
em (a, b), os valores de x que anulam f′(x) são, possivelmente, pontos extremos de f.
14 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

75. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios para a Determinação de Extremantes de uma Função Derivável
O teorema de Fermat nos garante que, se f é uma função definida em [a, b] e derivável
em (a, b), os valores de x que anulam f′(x) são, possivelmente, pontos extremos de f.
Observe que se x0 ∈ (a, b) é um extremo de f, então f′(x0) = 0 e na vizinhança de
x0 teremos sinais distintos para f′(x). Podemos, desta forma, concluir o resultado que
segue.
14 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

76. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios para a Determinação de Extremantes de uma Função Derivável
Theorem 6 (Critério da primeira derivada).
Se f : [a, b] → R é uma função contínua e derivável em ]a, b[ exceto,
possivelmente, em c ∈]a, b[.
I. Se f′(x) > 0, ∀ x < c e f′(x) < 0, ∀ x > c, então c é um ponto de máximo local
de f.
II. Se f′(x) < 0, ∀ x < c e f′(x) > 0, ∀ x > c, então c é um ponto de mínimo local
de f.
14 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

77. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios para a Determinação de Extremantes de uma Função Derivável
Theorem 6 (Critério da primeira derivada).
Se f : [a, b] → R é uma função contínua e derivável em ]a, b[ exceto,
possivelmente, em c ∈]a, b[.
I. Se f′(x) > 0, ∀ x < c e f′(x) < 0, ∀ x > c, então c é um ponto de máximo local
de f.
II. Se f′(x) < 0, ∀ x < c e f′(x) > 0, ∀ x > c, então c é um ponto de mínimo local
de f.
Demonstração: Ver Cálculo A, Flemming.
14 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

78. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios para a Determinação de Extremantes de uma Função Derivável
Esse teste estabelece essencialmente que se f for contínua em c e f′(x) mudar de sinal
positivo para negativa quando x cresce através de c, então f será um valor máximo
relativo em c, e se f′(x) mudar o sinal de negativo para positivo enquanto x cresce
através de c, então f terá um valor mínimo relativo em c.
14 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

79. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critérios para a Determinação de Extremantes de uma Função Derivável
Example 6.
Verifique quais pontos do domínio de cada função são extremantes.
a) f(x) = x4 − 4x3;
b) f(x) = x3 − 6x.
14 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

80. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

81. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Observando o gráfico da figura ao lado, temos que, numa
vizinhança de um ponto c de máximo local, as retas tan-
gentes à curva passam de coeficientes angular positivo (à
esquerda de c) para negativo (à direita de c). E o coefici-
ente angular é justamente a derivada de f.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

82. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Observando o gráfico da figura ao lado, temos que, numa
vizinhança de um ponto c de máximo local, as retas tan-
gentes à curva passam de coeficientes angular positivo (à
esquerda de c) para negativo (à direita de c). E o coefici-
ente angular é justamente a derivada de f.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

83. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Observando o gráfico da figura ao lado, temos que numa
vizinhança de um ponto c de mínimo local, as retas tan-
gentes à curva passam de coeficiente anular negativo (à
esquerda de c) para positivo (à direita de c).
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

84. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Observando o gráfico da figura ao lado, temos que numa
vizinhança de um ponto c de mínimo local, as retas tan-
gentes à curva passam de coeficiente anular negativo (à
esquerda de c) para positivo (à direita de c).
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

85. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Note que em ambos os casos f′(c) existe e é igual a 0.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

86. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Note que em ambos os casos f′(c) existe e é igual a 0.
Resumidamente, este teste estabelece essencialmente que se f for contínua em c e f′(x)
mudar de sinal positivo para negativo quando x cresce através de c, então f terá um
valor máximo relativo em c, e se f′(x) mudar o sinal de negativo para positivo enquanto
x cresce através de c, então f terá um valor mínimo relativo em c.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

87. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Example 7.
A função f(x) = (x − 2)3, esboçada na figura ao lado, mostra,
que mesmo f tendo ponto crítico, nesse caso em x = 2 e f′(x) > 0
quando x < 2 e f′(x) > 0 quando x > 2, ou seja, f não tem um
extremos relativo em 2.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

88. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Example 7.
A função f(x) = (x − 2)3, esboçada na figura ao lado, mostra,
que mesmo f tendo ponto crítico, nesse caso em x = 2 e f′(x) > 0
quando x < 2 e f′(x) > 0 quando x > 2, ou seja, f não tem um
extremos relativo em 2.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

89. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Example 7.
A figura ao lado, mostra um esboço de gráfico de uma
função f, que tem um valor máximo relativo num número c mas
f′(c) não existe, contudo f′(x) > 0 quando x < c e f′(x) < 0
quando x > c.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

90. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Example 7.
A figura ao lado, mostra um esboço de gráfico de uma
função f, que tem um valor máximo relativo num número c mas
f′(c) não existe, contudo f′(x) > 0 quando x < c e f′(x) < 0
quando x > c.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

91. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Em suma, para determinar os extremos relativos de uma f derivável:
Ache f′(x);
Ache os números críticos de f(x), isto é, os valores de x para os quais f′(x) = 0, ou
para os quais f′(x) não existe;
Aplique o teste da derivada primeira.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

92. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Em suma, para determinar os extremos relativos de uma f derivável:
Ache f′(x);
Ache os números críticos de f(x), isto é, os valores de x para os quais f′(x) = 0, ou
para os quais f′(x) não existe;
Aplique o teste da derivada primeira.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

93. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Interpretação Geométrica
Em suma, para determinar os extremos relativos de uma f derivável:
Ache f′(x);
Ache os números críticos de f(x), isto é, os valores de x para os quais f′(x) = 0, ou
para os quais f′(x) não existe;
Aplique o teste da derivada primeira.
15 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

94. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
16 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

95. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Example 7.
Dada f(x) = x3 − 6x2 ache os extremos relativos de f, aplicando o teste da
derivada primeira. Determine os valores de x nos quais ocorrem extremos relativos,
bem como os intervalos nos quais f é crescente e aqueles onde f é decrescente. Faça
um esboço do gráfico.
16 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

96. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Solução: Temos que f′(x) = 3x2 − 12x e f′(x) existe para todos os valores de x. f′(x) =
0 ⇔ 3x2 − 12x = 0 ⇔ 3(x − 3)(x − 1) = 0 ⇔ x = 3 ou x = 1.
16 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

97. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Solução: Temos que f′(x) = 3x2 − 12x e f′(x) existe para todos os valores de x. f′(x) =
0 ⇔ 3x2 − 12x = 0 ⇔ 3(x − 3)(x − 1) = 0 ⇔ x = 3 ou x = 1.
Assim, os números críticos de f são 1 e 3. Para determinar se o gráfico de f tem um
extremo relativo nestes valores de x encontrados, aplicamos o teste da primeira derivada,
conforme o quadro abaixo.
16 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

98. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
f(x) f′(x) Conclusão
x < 1 f é crescente
x = 1 5 0 f tem um valor máximo relativo
1 < x < 3 − f é decrescente
x = 3 1 0 f tem um valor mínimo relativo
x > 3 f é crescente
16 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

99. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
f(x) f′(x) Conclusão
x < 1 f é crescente
x = 1 5 0 f tem um valor máximo relativo
1 < x < 3 − f é decrescente
x = 3 1 0 f tem um valor mínimo relativo
x > 3 f é crescente
y
0 1 2 3 4 5
−1
0
−1
1
2
3
4
5
16 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

100. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

101. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Com o teste da derivada primeira, podemos determinar se uma função f tem valor
máximo ou mínimo relativo num número crítico c, verificando o sinal de f′ em números
contidos em intervalos à direita e à esquerda de c. Veremos a seguir, outro teste para
extremos relativos envolvendo somente o número crítico c.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

102. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Com o teste da derivada primeira, podemos determinar se uma função f tem valor
máximo ou mínimo relativo num número crítico c, verificando o sinal de f′ em números
contidos em intervalos à direita e à esquerda de c. Veremos a seguir, outro teste para
extremos relativos envolvendo somente o número crítico c.
Theorem 7 (Critério da segunda derivada).
Sejam f : [a, b] → R uma função contínua e derivável até segunda ordem em
(a, b), com derivadas f′ e f′′ também contínuas em I e c ∈ I tal que f′(c) = 0. Então,
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

103. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Com o teste da derivada primeira, podemos determinar se uma função f tem valor
máximo ou mínimo relativo num número crítico c, verificando o sinal de f′ em números
contidos em intervalos à direita e à esquerda de c. Veremos a seguir, outro teste para
extremos relativos envolvendo somente o número crítico c.
Theorem 7 (Critério da segunda derivada).
Sejam f : [a, b] → R uma função contínua e derivável até segunda ordem em
(a, b), com derivadas f′ e f′′ também contínuas em I e c ∈ I tal que f′(c) = 0. Então,
(1) se f′′(c) < 0, c é ponto de máximo local;
(2) se f′′(c) > 0, c é ponto de mínimo local.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

104. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Observação: Que o teste falha quando f′′(x) = 0 pode-se ver facilmente nos gráficos
que iremos exibir a seguir. Logo se f′′(c) = 0 e nada se conclui quanto a máximo e
mínimo relativos, deve–se usar o teste da derivada primeira.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

105. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Observação: Que o teste falha quando f′′(x) = 0 pode-se ver facilmente nos gráficos
que iremos exibir a seguir. Logo se f′′(c) = 0 e nada se conclui quanto a máximo e
mínimo relativos, deve–se usar o teste da derivada primeira.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

106. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Considerando as funções y = x4, y = −x4 e y = x3, notemos que cada uma delas
possui a segunda derivada nula em x = 0. Em x = 0, a função y = x4 possui um
mínimo relativo, e y = −x4 possui um máximo relativo, no entanto, para y = x3 não
tem máximo e nem mínimo relativo.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

107. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Example 7.
Dada f(x) = x2 − 4x − 5, usar o teste da derivada segunda para obter o máximo
ou o mínimo relativos.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

108. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Example 7.
Dada f(x) = x2 − 4x − 5, usar o teste da derivada segunda para obter o máximo
ou o mínimo relativos.
Solução: Temos que f′(x) = 2x−4 = 0 ⇔ x = 2. Como f′′(x) = 2, logo como f′′(2) > 0
e f′(2) = 0, existe um mínimo relativo quando x = 2. Esse valor é −9.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

109. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Example 7.
Dada f(x) = x3 + x2 − 8x − 1, usar o teste da derivada segunda para obter o
máximo ou o mínimo relativos.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

110. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Um Segundo Teste para Máximos e Mínimos Relativos
Example 7.
Dada f(x) = x3 + x2 − 8x − 1, usar o teste da derivada segunda para obter o
máximo ou o mínimo relativos.
Solução: Temos que f′(x) = 3x2 + 2x − 8 = 0 ⇔ (3x − 4)(x + 2) = 0 ⇔ x =
4
3
ou
x = −2.
Como f′′(x) = 6x segue que f′′(−2) < 0 e f′′
(
4
3
)
> 0. Portanto, existem um máximo
relativo para x = −2 e um mínimo relativo para x =
4
3
.
17 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

111. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critério Geral para Determinar Extremantes
18 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

112. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critério Geral para Determinar Extremantes
Theorem 8.
Sejam f uma função derivável até n-ésima ordem em I =]a, b[ e x0 ∈ I tal que
f′(x0) = f′′(x0) = . . . = f(n−1)(x0) = 0;
f(n)(x0) ̸= 0.
Então
se n é par e
{
f(n)
(x0) < 0 , x0 é ponto de máximo local de f;
f(n)
(x0) > 0 , x0 é ponto de mínimo local de f;
se n é ímpar, x0 não é ponto de máximo local nem de mínimo local de f.
18 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

113. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critério Geral para Determinar Extremantes
Example 8.
Verifique quais os pontos extremantes da função f(x) = x5 − 3x4 + x3 − x2.
18 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

114. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critério Geral para Determinar Extremantes
Solução: f(x) = x5 − 3x4 + x3 − x2 ⇒ f′(x) = 5x4 − 12x3 + x2 − 2x = x(x − 1)2(5x − 2),
f′′(x) = 20x3 − 36x2 e f′′′(x) = 60x2 − 72x.
18 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

115. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critério Geral para Determinar Extremantes
Solução: f(x) = x5 − 3x4 + x3 − x2 ⇒ f′(x) = 5x4 − 12x3 + x2 − 2x = x(x − 1)2(5x − 2),
f′′(x) = 20x3 − 36x2 e f′′′(x) = 60x2 − 72x.
Os possíveis extremantes de f são obtidos ao resolvermos a equação f′(x) = 0.
18 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

116. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critério Geral para Determinar Extremantes
Solução: f(x) = x5 − 3x4 + x3 − x2 ⇒ f′(x) = 5x4 − 12x3 + x2 − 2x = x(x − 1)2(5x − 2),
f′′(x) = 20x3 − 36x2 e f′′′(x) = 60x2 − 72x.
Os possíveis extremantes de f são obtidos ao resolvermos a equação f′(x) = 0.
As raízes destas equações são: x = 0, x = 1 e x =
2
5
.
18 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

117. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Critério Geral para Determinar Extremantes
Solução: f(x) = x5 − 3x4 + x3 − x2 ⇒ f′(x) = 5x4 − 12x3 + x2 − 2x = x(x − 1)2(5x − 2),
f′′(x) = 20x3 − 36x2 e f′′′(x) = 60x2 − 72x.
Os possíveis extremantes de f são obtidos ao resolvermos a equação f′(x) = 0.
As raízes destas equações são: x = 0, x = 1 e x =
2
5
.
x f′(x) f′′(x) f′′′(x) Conclusão
0 0 −2 ponto de máximo
1 0 0 6 não é extremante
2
5
18
25 ponto de mínimo
18 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

118. A derivada e os extremantes de uma função
O Teorema de Fermat
O Teorema de Rolle
O Teorema de Lagrange
Referências
M. B. Gonçalves and D. M. Flemming.
Cálculo A.
Pearson Education, 5 edition, 2007.
H. L. Guidorizzi.
Um curso de cálculo, volume 1.
Grupo Gen-LTC, 5 edition, 2000.
A. Howard.
Cálculo, um novo horizonte, volume 1.
Bookman, Porto Alegre, 2000.
E. L. Lima.
Curso de Análise, volume 1.
IMPA, Rio de Janeiro, 2000.
J. Stewart.
Cálculo, volume 1.
Cengage Learning, São Paulo, 6 edition, 2009.
19 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022