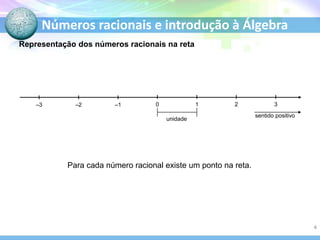
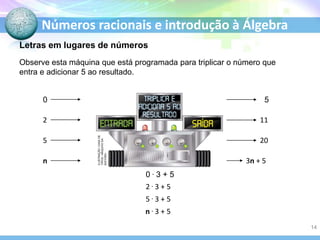
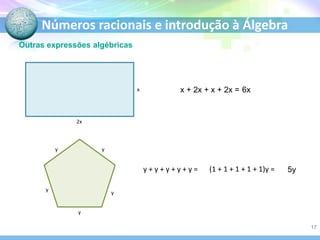
O documento discute números racionais e introdução à álgebra. Ele explica como números racionais podem ser escritos como frações ou decimais periódicos, define o conjunto dos números racionais, e discute representações na reta real, módulo, oposto, comparação e operações com números racionais. Também introduz expressões algébricas, equações e resolução de equações do primeiro grau.

1. Números racionais e
introdução à Álgebra

2. Números racionais e introdução à Álgebra
Todo número racional pode ser escrito na forma de um número decimal,
por meio de número decimal exato ou de uma dízima periódica.
Exemplos:
= =
= 5 =
0,75 0,333... –0,5
Identificação dos números racionais
3 4
0 7
0
,
2 0
− 2 0
5
3 0
− 2 8
1 3
0 3
1
,
1 0
− 0 9
3
1 0
− 0 9
2

3. Números racionais e introdução à Álgebra
O conjunto dos números racionais é formado por todos os números que podem
ser escritos na forma de fração e é representado por:
tal que pertence Inteiro diferente de zero
–7
O conjunto dos números racionais ( )
x | x = , com p e q *
=
A relação entre os conjuntos , , e
1
3

4. Números racionais e introdução à Álgebra
Representação dos números racionais na reta
Para cada número racional existe um ponto na reta.
0 1 2 3
‒3 ‒2 ‒1
unidade
sentido positivo
4

5. Números racionais e introdução à Álgebra
Módulo ou valor absoluto de um número racional
Chamamos de módulo ou valor absoluto de um número racional a distância do ponto
que representa esse número até a origem.
0 +1
‒1
A B
O
‒ ‒ +
+
da unidade da unidade
=
‒ =
+ =
+
5

6. Números racionais e introdução à Álgebra
Oposto ou simétrico de um número racional
• oposto de – 2,3 é 2,3
• o simétrico de 0,5 é – 0,5
• oposto de é −
0 1 2 3
‒3 ‒2 ‒1
2,3
−2,3
−
6

7. Números racionais e introdução à Álgebra
Comparação de dois números racionais
Comparar dois números significa dizer se o primeiro é maior do que (>),
menor do que (<) ou igual (=) ao segundo número.
Um número negativo, sempre é menor que o 0 (zero) e que um número positivo.
• – 0,4539 < 0,1 • – 99,5 < +2 • – 0,00002 < 0
Ao comparar dois números negativos, o que tiver o módulo maior é o menor
dos dois.
• – 27,56 < – 2,4 , pois: |– 27,56| = 27,56 e | – 2,4 | = 2,4
Ao comparar dois números positivos, o que tiver o módulo maior é o maior
dos dois.
• + 17,5 > + 10,5 pois: |+ 17,5| = 17,5 e |+ 10,5| = 10,5
7

8. Números racionais e introdução à Álgebra
Operações com números racionais
8
Adição algébrica de número racionais
(–2,3) + (–4,5) = –2,3 – 4,5 = –6,8
Multiplicação de números racionais
. = – =
(– 0,5) . (– 2,4) = +1,2
Exemplos:
Exemplos:
– = + = = =
–

9. Números racionais e introdução à Álgebra
Inverso de um número racional
O produto de um número racional e o seu inverso é +1.
Exemplos:
. = = = 1
Aplicando o mesmo raciocínio, o inverso de – é – e o produto entre eles é:
– . = = 1
O inverso de é e o produto entre eles é:
9

10. Números racionais e introdução à Álgebra
Divisão de números racionais
Exemplos:
: = . = = =
= .
=
Para dividir um número racional por outro, multiplica-se o
primeiro pelo inverso do segundo.
=
10

11. Números racionais e introdução à Álgebra
Raiz quadrada exata de número racional
Exemplos:
= , pois =
é impossível em , pois não existe número
racional que elevado ao quadrado dê –0,25.
= = = = 1,1
11
Link para
ambiente online

12. Números racionais e introdução à Álgebra
Potenciação com número racional na base e número natural no expoente
Exemplos:
(– 0,1)3 = (– 0,1) . (– 0,1) . (– 0,1) = – 0,001
= . = +
Propriedades da potenciação de números racionais
1a propriedade: am . an =
2a propriedade: am : an =
4a propriedade: (a . b)m =
3a propriedade: (am)n =
am + n
am - n
am . n
am . bm
=
a , b e m naturais
a , m e n naturais
a *, m e n naturais
a , m e n naturais
12

13. Números racionais e introdução à Álgebra
Potência de base 10
103 = 1 000 (1 seguido de três zeros)
105 = 100 000 (1 seguido de cinco zeros)
10−1 = = 0,1
10 −3 = = 0,001
A notação ou escrita científica
Características:
• Ser escrito como um produto de dois fatores;
• Um dos fatores deve ser um número de 1 a 9;
• O outro fator deve ser uma potência de base 10.
Exemplo: Urano é o sétimo planeta a ter um Sistema Solar e sua distância
média do Sol é de 2 870 000 000 km.
2 870 000 000 = 287 . 10 000 000 = 2,87 . 100 . 10 000 000 =
= 2,87 . 102 . 107 = 2,87 . 109
13
Link para
ambiente online

14. Números racionais e introdução à Álgebra
Observe esta máquina que está programada para triplicar o número que
entra e adicionar 5 ao resultado.
0 5
0 . 3 + 5
2
2 . 3 + 5
11
5
5 . 3 + 5
20
n
n . 3 + 5
3n + 5
Letras em lugares de números
ILUSTRAÇÃO:
CASA
DE
TIPOS
/
ARQUIVO
DA
EDITORA
14

15. Números racionais e introdução à Álgebra
São exemplos de expressões algébricas:
x ou 1x 2x x – 3
Expressões que contêm números e letras são chamadas de expressões
algébricas.
Partes de uma expressão algébrica
2x + 9
2x: termo algébrico
9: termo numérico
• 2x
Coeficiente: 2
Parte literal: x
• a
Coeficiente: 1
Parte literal: a
Exemplos:
Parte literal: xy2
Expressões algébricas
• – xy2
Coeficiente: −
15

16. Números racionais e introdução à Álgebra
Termos algébricos semelhantes
Termos algébricos semelhantes são aqueles que possuem a
mesma parte literal.
Exemplos:
5b + 4b = 9b
–2x2y + 5x2y = 3x2y
–2 + 5 = 3
=
+
16

17. Números racionais e introdução à Álgebra
Outras expressões algébricas
x + 2x + x + 2x = 6x
y + y + y + y + y = (1 + 1 + 1 + 1 + 1)y = 5y
x
2x
y
y
y y
y
17

18. Números racionais e introdução à Álgebra
Expressões algébricas equivalentes
Uso da propriedade distributiva
2x + 6x = (2 + 6) . x = 8 . x = 8x
3y + 5y + y = (3 + 5 + 1) . y = 9 . y = 9y
3(x + 4) = 3 . x + 3 . 4 = 3x + 12
18

19. Números racionais e introdução à Álgebra
Valor numérico de uma expressão algébrica
Valor numérico de uma expressão algébrica é o valor que ela assume
quando substituímos cada letra por um número e efetuamos as
operações indicadas.
Exemplos:
, para x = 5 = 5 : 2,5 = 2
12y, para y = 12 . = = 6
t + 10, para t = –10 –10 + 10 = 0
19

20. Números racionais e introdução à Álgebra
Uso de letras para encontrar números desconhecidos
Exemplo:
Qual é a idade atual de Pedro se daqui a 8 anos ele terá 31 anos?
x + 8 = 31
Indicamos por x a
idade atual de Pedro
Para encontrar o valor de x, devemos desfazer a adição pela
operação inversa, que é a subtração.
x = 31 – 8
x = 23
Portanto, a idade atual de Pedro é 23 anos.
20

21. Números racionais e introdução à Álgebra
Equações são igualdades que contêm pelo menos uma letra que representa
um número desconhecido.
Exemplos de equações: • 3x – 1 = 8
• x + y = 10
• r2 + 1 = r + 13
As propriedades da igualdade
4 + 5 . 2 14 + 0
1o membro
=
2o membro
4 + 10 14
14
3 + 4 – 2 + 9
1o membro
=
2o membro
7 7
Equação, incógnita e solução ou raiz
21

22. Números racionais e introdução à Álgebra
Uma equação é do 1o grau com uma incógnita (x) quando pode ser escrita
na forma ax = b, com a ≠ 0.
Resoluções de equações do 1o grau com uma incógnita
3n + 10 = 91
3n + 10 – 10 = 91 – 10
3n = 81
n = 27
y = 32
Solução ou raiz da equação
Equações do 1o grau com uma incógnita
. 3n = 81 .
=
Solução
ou raiz da
equação
– 5 = 11
– 5 + 5 = 11 + 5
= 16
2 . = 16 . 2
= 16 . 2
22

23. Números racionais e introdução à Álgebra
Explorando a ideia de equilíbrio e resolvendo equações do
1o grau com uma incógnita
5x + 50 = 3x + 290
5x = 3x + 240
2x = 240
x = 120
x =
PAULO MANZI / ARQUIVO DA EDITORA
23

24. Números racionais e introdução à Álgebra
Equações com frações
12x + x = 104
13x = 104
x = 8
mmc (1, 4, 1) = 4
Equações com parênteses
5(x – 2) = 4 – (– 2x + 1)
5x – 10 = 4 + 2x – 1
5x – 10 = 3 + 2x
5x = 3 + 2x + 10
5x = 13 + 2x
5x – 2x = 13
3x = 13
3x + = 26
+ =
+ =
x =
x =
dividindo ambos os
membros por 13
24

25. Números racionais e introdução à Álgebra
Dízimas periódicas simples
0,777... = ?
x = 0,777...
10x = 7,777...
10x = 7 + 0,777...
x
10x = 7 + x
10x – x = 7
9x = 7
Portanto a fração geratriz de 0,777... é .
Regra prática:
0,142142... =
3 algarismos
0,666... =
1 algarismo
x =
Uma aplicação de equação: geratriz de uma dízima periódica
25

26. Números racionais e introdução à Álgebra
Dízimas periódicas compostas
0,2555... = ?
x = 0,2555...
10x = 2,555...
90x = 18 + 5
90x = 23
10x = 2 + 0,555...
10x = 2 +
x =
Portanto a fração geratriz de 0,2555... é .
26