[1] O documento discute as leis de Newton da dinâmica, incluindo as leis da inércia, da aceleração e da ação e reação. [2] É explicado o conceito de forças como peso, normal, tensão e elástica. [3] Os conceitos de trabalho, potência, energia cinética e potencial são introduzidos em relação ao movimento retilíneo uniforme e variado.

1. Dinâmica
Prof. Fabricio Scheffer

2. Leis de Newton
1ª Lei de Newton
Repouso
a =0
Inércia  Todo corpo tem uma tendência em ficar
FR = 0
MRU
Só sai desses estados se uma FR  0 atuar no corpo
MRU  Velocidade constante
MRU  Trajetória reta

3. 2ª Lei de Newton  Princípio Fundamental da Dinâmica (P.F.D.)
“Quando uma força resultante é aplicada a um corpo ela produz, na sua
direção e sentido, uma aceleração, com intensidade proporcional a
intensidade da força resultante.”
a  1
a  FR
a = FR
m
ou
FR = m a
Newton (N)
kg
m/s2
Unidades no S.I.
m

4. Tipos de Força
 Força Peso (P):
Força de atração
gravitacional que um planeta
exerce sobre um corpo
P=m.g
 Força Normal (FN)
Força que a superfície faz sobre o corpo.
É aplicada sempre 90° à superfície

5.  Tensão ou Tração (T)
Força que existe entre um cabo
ou corda e um corpo.
 Força elástica
Força que uma mola exerce sobre um corpo.
lei de Hooke:
Fe = K.X

6.  Força de Atrito
Força de atrito estático (fe)
FR = 0 ; F = fe
Força de Atrito Estático máxima (femáx)
Valor da força a ser ultrapassado para
que o bloco inicie o deslizamento sobre a
superfície.
Femáx = me . FN
Força de Atrito Cinético (fc)
Existe quando o bloco está em movimento sobre a
superfície.
O valor da fc, independentemente do valor da velocidade
do corpo, é sempre calculado da seguinte forma:
fc = mc . FN
sendo que mc < me

7. 3ª Lei de Newton  Ação e Reação
A 3ª Lei de Newton, também chamada Princípio da Ação e Reação,
estabelece como se desenvolvem as interações (troca de forças) entre dois
corpos.
“A toda força de ação (F) corresponde a uma força de reação (-F) com a
mesma intensidade, mesma direção e sentido oposto.”

8. Características das forças de Ação e Reação:
• Ação e Reação tem mesmo módulo  FAB = FBA
•Ação e Reação tem mesma direção
•Ação e Reação tem sentidos opostos
•Ação e Reação estão SEMPRE em corpos diferentes (NUNCA se anulam)

9. Força Centrípeta (FC)
MCU
A força resultante é centrípeta
Aceleração centrípeta:
V2
aC 
R
Força centrípeta:
Fc = m . ac
V2
FC  m
R

10. Ao romper a corda, cessa a tensão (força centrípeta) e o corpo sai pela tangente

11. Ao cessar a força centrípeta
(que é uma força de
aderência) o alimento sai
peça tangente
Existe força de centrípeta
(aderência) durante todo trajeto

12. Plano Inclinado
Forças Atuantes:
P
Px = P sen a
Py = P cos a
FN= Py
Fat =m . N

13. Trabalho de forças mecânicas (gasto de energia)
Trabalho de uma Força Constante
Trabalho Nulo (W = 0)
F
a) | F | = 0 (não há força)
q
d
b) | d | = 0 (não há deslocamento)
c) cos q = 0 (F perpendicular a d)
WF = | F | . | d | . COS q
Importante:
O trabalho da força peso e força normal no deslocamento horizontal é igual a zero.
O trabalho de uma força conservativa não depende da trajetória.
A força centrípeta não realiza trabalho, pois é perpendicular a trajetória.

14. Trabalho de uma Força variável - Método Gráfico
A = WFR
WOA positivo
WAB  negativo
WFR  WOA + WAB

15. Trabalho da Força Peso
a) Na descida: WP = + P h = + m g h
b) Na subida: WP = - P h = - m g h

16. Potência
Potência é a medida da rapidez que o trabalho é realizado.
WF
Pot 
t
Pot  F  Vm
Unidade:
1J
1W 
1s

17. Teorema da Energia Cinética
WFR  EC
m V
EC 
2
2
2
m  V 2 m  V0
WFR 

2
2

18. Energia Mecânica (EM)
EM  E C  EP
Potencial
(armazenada)
Cinética
(movimento)
m  V2
EC 
2
Gravitacional
(altura)
EP  m  g  h
g
Elástica
(mola deformada)
EP
e
KX

2
2

19. Sistema de Forças Conservativas
Um sistema de forças e dito conservativo quando não altera a energia
mecânica do corpo sobre o qual o sistema atua.
EM = EC + EP = constante
Não há atritos
EMA = EMB
Qual tipo de questão usar a conservação de Energia Mecânica?
Dado (A)
Pedido (B)
V
V
h
h
x
x

20. Sistema de Forças NÃO-Conservativas
W fat  EM
W fat   EM Dissipada

21. KE= energia cinética
GPE= energia potencial gravitacional

24. EM é constante, EPg
se transforma em
EC e vice-versa
EM se transforma
em calor, pois há
atrito.

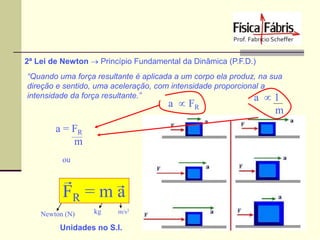
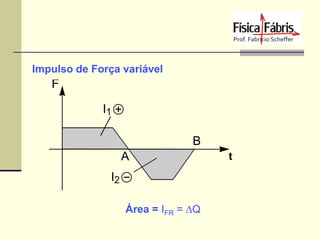
25. Impulso de Força Constante
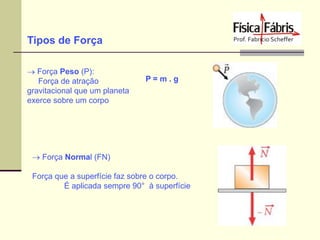
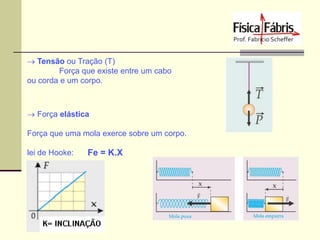
I = F . t
[N . s]
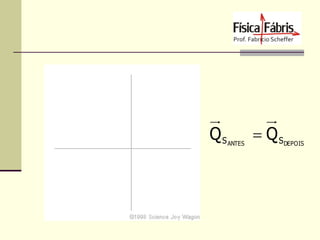
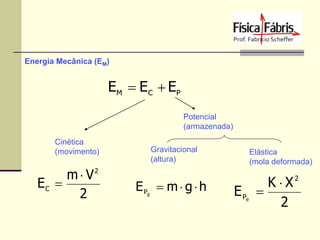
Quantidade de Movimento (Momentum Linear)
Q=mV
[kg . m/s]
Teorema do Impulso
IFR = Q
IFR = m (V – Vo)
Note que os três
possuem as mesmas
velocidade iniciais e
finais (mesmo Q), ou
seja, mesmo impulso

26. Impulso de Força variável
t
Área = IFR = Q

27. Calcule a quantidade de movimento nas situações I e II
I)
II)
V  5m / s
2 kg
As quantidades de movimentos I e II são iguais ?
V  2m / s
5 kg
Não, pois os sentidos são opostos. Apenas
o módulo é o mesmo

28. Colisões e Explosões (FRext=0)
QS
ANTES
 QS
DEPOIS

29. QS
ANTES
 QS
DEPOIS

30. QS
ANTES
 QS
DEPOIS
O corpo de menor massa necessita de maior velocidade par ter a
mesma quantidade de movimento (em módulo) que o de maior massa.

32. Tipos de Colisão
Parcialmente inelástica
Com deformação, mas não
permanecem juntos
inelástica
Com deformação, e permanecem
juntos (máxima perda de energia)
Elástica
Sem deformação, não há
perda de energia.
Em todas colisões
QS
ANTES
 QS
DEPOIS