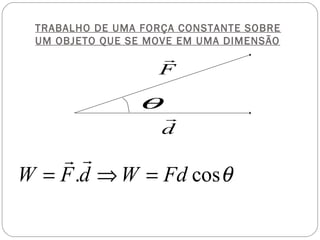
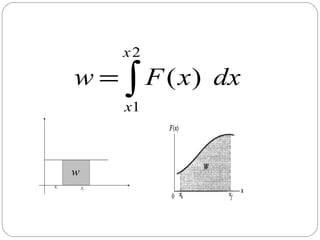
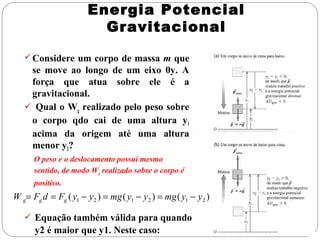
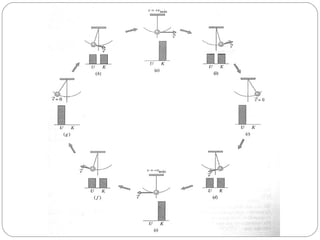
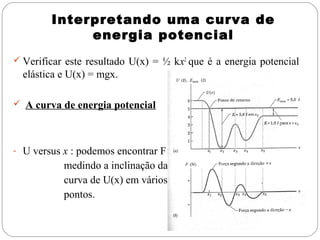
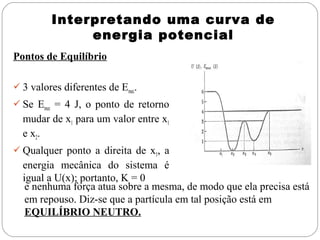
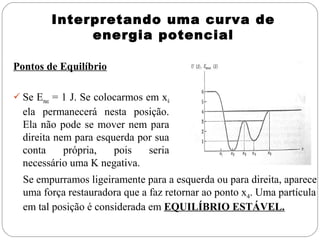
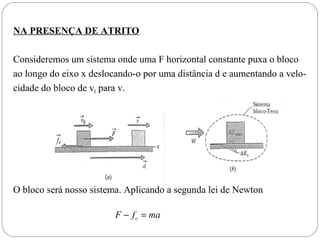
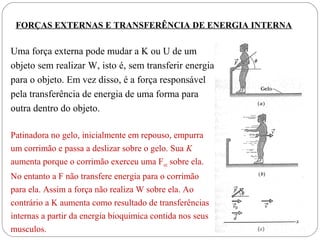
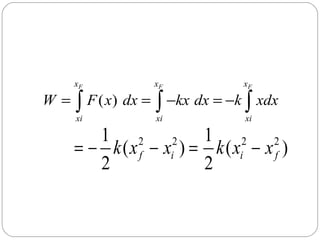Energia potencial é a energia associada com a posição de um objeto em um sistema. Existem dois tipos principais: energia potencial gravitacional, relacionada à altura acima do solo, e energia potencial elástica, relacionada à compressão ou estiramento de um mola. A soma da energia cinética e potencial de um sistema fornece a energia mecânica total, que se mantém constante de acordo com a lei da conservação da energia.