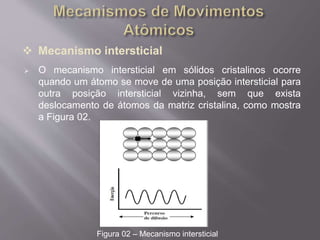
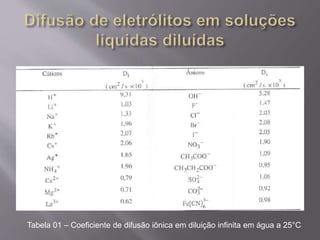
O documento discute os mecanismos de difusão atômica em sólidos, incluindo difusão por substituição, intersticial e em anel. A difusão depende de fatores como temperatura, estrutura cristalina, defeitos e energia de ativação. A difusão em sólidos porosos e de eletrólitos em soluções também é abordada.

1. UNIVERSIDADE FEDERAL DE CAMPINA GRANDE
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR
UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS
CAMPUS DE POMBAL – PB
Discente: Anderson dos Santos Formiga
Disciplina: Fenômenos de Transporte II
Doscente: Georgiana Maria Vasconcelos
Martins

2.  A difusão atômica pode ser definida como um
mecanismo pelo qual a matéria é transportada através
da matéria.
 Os átomos em gases, líquidos e sólidos estão em
constante movimento.
 No caso dos sólidos, o movimento atômico é bastante
restrito, em função das elevadas forças de ligação
atômica e da existência de posições de equilíbrio bem
definidas. Todavia, as vibrações atômicas de origem
térmica existentes em sólidos permitem movimentos
atômicos limitados.

3.  A difusão atômica em metais e ligas é
particularmente importante, pois a maioria das
reações no estado sólido, que são
fundamentais em metalurgia, envolve
movimentos atômicos.
 Exemplos de reações de estado sólido
ocorrem: na nucleação e crescimento de novas
fases em sólidos cristalinos, na cementação
dos aços, na produção de semicondutores
(difusão de dopantes) etc.

4.  Em um cristal, os átomos somente ficam estáticos
no zero absoluto (-273ºC). Nestas condições, os
átomos permanecem na posição correspondente ao
mínimo de energia.
 Acima desta temperatura os átomos começam a
vibrar e, à medida que a temperatura se eleva, as
vibrações térmicas tornam-se mais intensas,
fazendo com que os átomos se dispersem ao acaso
em torno da posição de menor energia.
 Deslocamentos atômicos podem também ocorrer
sob ação de campos elétricos ou magnéticos, se as
cargas dos átomos interagem com o campo (átomos
na forma de íons são facilmente deslocados em um
campo elétrico).

5.  Existem dois mecanismos básicos de difusão
de átomos em um sólido cristalino, e ambos
envolvem defeitos pontuais:
 Mecanismo substitucional ou de vazios ;
 Mecanismo intersticial.
 Além desses dois, o movimento atômico pode
se dá por meio do mecanismo de anel, de
ocorrência mais difícil, pois envolve maior
gasto de energia.

6.  Mecanismo substitucional ou de vazios
 Os átomos podem mover-se no interior do cristal, de
uma posição atômica para outra, se apresentarem
energia de vibração suficiente e se existirem
posições atômicas vazias (lacunas) ou outros
defeitos cristalinos na estrutura atômica.
 Em metais, com o aumento da temperatura, mais
lacunas podem ser observadas (a concentração de
vacâncias é termicamente ativada) e mais energia
térmica estará disponível. Assim, a taxa de difusão
atômica aumentará com a temperatura.

7.  Mecanismo substitucional ou de vazios
 Na Figura 01, se um átomo próximo à lacuna tem
energia suficiente, ele poderá mover-se até essa
posição vazia.
Figura 01 – Mecanismos de vazios

8.  Mecanismo intersticial
 Para que o mecanismo de difusão intersticial seja
ativo, o tamanho do átomo em difusão deve ser
pequeno comparativamente aos átomos da matriz.
 Pequenos átomos como o hidrogênio, o carbono,
o nitrogênio e o oxigênio podem apresentar
difusão intersticial em alguns sólidos cristalinos.

9.  Mecanismo intersticial
 O mecanismo intersticial em sólidos cristalinos ocorre
quando um átomo se move de uma posição intersticial para
outra posição intersticial vizinha, sem que exista
deslocamento de átomos da matriz cristalina, como mostra
a Figura 02.
Figura 02 – Mecanismo intersticial

10. Mecanismo de difusão em anel
 A difusão em anel envolve o movimento simultâneo de três ou
quatro átomos, como mostra a Figura 03. Este mecanismo é
mais raro devido às suas particularidades.
 Uma simples troca entre dois átomos vizinhos é teoricamente
possível; entretanto, seria mais difícil que a difusão em anel,
em função da necessidade de altos níveis de energia para
ocorrer.
Figura 03 - Mecanismo de difusão em anel. (a) Anel de três átomos; (b) anel de quatro
átomos.

11.  Em condições uniformes, cada um dos átomos
adjacentes à lacuna tem a mesma probabilidade de
se mover para ela. Analogamente, o átomo
intersticial tem a mesma probabilidade de se mover
em cada um dos interstícios à sua volta.
 Se os átomos devem mudar de posições, as “barreiras
de energia” devem ser superadas.
 Energia de ativação é a energia requerida para
superar tais barreiras, somada à energia de formação
do defeito, quando houver.

12.  Portanto, necessita-se de energia para retirar o
átomo dos seus vizinhos originais. A energia de
ativação varia com diversos fatores. Por exemplo:
 Um átomo pequeno tem uma energia de ativação
menor que um átomo grande ou molécula;
 Os movimentos intersticiais requerem mais energia
que os movimentos de vazios;
 São necessárias elevadas energias de ativação para
a difusão em materiais fortemente ligados e de alto
ponto de fusão, como o tungstênio, o carbeto de
boro e outros.

13.  A análise estatística de Boltzmann aplicada ao
movimento atômico permite estabelecer a intensidade de
difusão atômica em materiais.
 A difusão de um material A (soluto) dentro da estrutura de
um material B (solvente) é representada pelo coeficiente
de difusão (D), definido pela equação de Arrhenius:
onde D = coeficiente de difusão; Do=
constante do sistema soluto/solvente; Q =
energia de ativação; R = constante molar dos
gases (8,314 J/mol.K ou 1,987 cal/mol.K); T =
temperatura absoluta.

14.  A difusividade atômica depende de diversos fatores,
sendo que os mais importantes são:
 Tipo de mecanismo de difusão: Dependendo dos
tamanhos atômicos envolvidos, o mecanismo de difusão
influencia a intensidade de difusão (átomos de tamanhos
próximos têm difusão elevada quando o mecanismo é
substitucional; quando os átomos apresentam tamanhos
muito diferentes, o mecanismo apropriado é o intersticial);
 Temperatura na qual a difusão ocorre
 Tipo de estrutura cristalina do solvente: Estruturas
compactas (CFC e HC) dificultam a difusão atômica por
serem mais compactas;
 Tipo e quantidade de imperfeições presentes na rede
cristalina: Defeitos como discordâncias e lacunas
aumentam a intensidade de difusão.

15.  Alguns processos (por ex.: purificação de gases) exigem
a utilização de adsorventes que apresentam poros
seletivos a um determinado gás (peneiras moleculares).
 Podemos notar, então, que qualquer que seja o processo,
o soluto (gasoso ou líquido) difunde por uma matriz onde
a configuração geométrica é determinante para o
fenômeno de difusão.
Figura 04 – Difusão em sólidos porosos

16.  A difusão em um sólido poroso apresenta
distribuição de poros e geometria externas
peculiares que determinam a mobilidade do
difundente, sendo classificadas como:
 Difusão de Fick;
 Difusão de Knudsen;
 Difusão configuracional.

17.  Difusão de Fick
 Difusão de um soluto em um sólido com poros
relativamente grandes, maiores do que o caminho livre
média das moléculas difundentes, sendo descrita de
acordo com a primeira lei de Fick em termos de
coeficiente e efetivo de difusão:

18.  Difusão de Fick
 O coeficiente efetivo (Def) aparece em razão da
tortuosidade do sólido poroso. Ele depende das
variáveis que influenciam a difusão como, T, P e das
propriedades da matriz porosa: porosidade ( 휀푝) ,
esfericidade (Φ) e a tortuosidade (τ).

19. Difusão de Knudsen
 Quando se trata de gases leves, pressão baixa ou poros
estreitos, o soluto irá colidir com as paredes dos poros ao
invés de colidir com outras moléculas, de modo a ser
desprezível o efeito de corrente das colisões entre as
moléculas no fenômeno difusivo. Neste caso, cada
molécula se difunde independente das demais. Neste
caso, o coeficiente é análogo ao obtido pela teoria
cinética dos gases:
onde,
Ω - Velocidade média molecular
푑푝 – diâmetro médio dos poros

20. Difusão de Knudsen
 Quando a tortuosidade é considerada na
difusão de Knudsen, o coeficiente
fenomenológico é corrigido para:

21. Difusão configuracional
 A difusão configuracional ocorre em matrizes
porosas, macro- e mesoporosas devido aos
saltos energéticos do soluto pelos microporos.
A difusão é dada por:

22.  Os eletrólitos constituem-se de solução
composta de solvente, normalmente água, na
qual uma determinada substância decompõe-se
em íons, como por exemplo a dissolução de
sais.
 Quando se dissolve o sal de cozinha (NaCl)
em água, não ocorre a difusão da “molécula”
de sal, há a sua dissolução nos íons 푁푎+
(cátion) e 퐶푙−(ânion) , os quais difundirão como
se fossem “moléculas” independentes , mas
fluindo na mesma direção.

23.  As velocidades dos íons são descritas
analogamente à teoria de Stokes-Einstein.
 Em se tratando de eletrólitos, a velocidade do íon
está associada tanto com o potencial químico
quanto com o eletrostático.
(Velocidade) = (mobilidade)[diferença de potencial
químico) + (diferença de potencial eletrostático)]

24. Obtenção do coeficiente de difusão de eletrólitos em soluções
líquidas diluídas
Ex: Estime o valor do coeficiente de difusão em diluição
infinita a 25°C do NaCl em água.
NaCl  푁푎+1 + 퐶푙−1 ; Z1= +1 e Z2 = -1

25. Tabela 01 – Coeficiente de difusão iônica em diluição infinita em água a 25°C

26. Obtenção do coeficiente de difusão de eletrólitos em
soluções líquidas diluídas
Da tabela 01 temos que:
D1 = 퐷푁푎+ = 1,33x10−5 푐푚2/s
e D2 = 퐷퐶푙− = 2,03x10−5 푐푚2/s
퐷0퐴 =[
(⃓+1⃓ +⃓−1⃓)(1,33)(2,03)
(⃓+1⃓ 1,33 + ⃓−1⃓(2,03))
]x10−5 = 1,607 x 10−5 푐푚2/s

27.  A difusão de eletrólitos em soluções líquidas
concentradas apresenta o mesmo problema da difusão
de não-eletrólitos em líquidos concentrados, não há,
no momento, teoria capaz de descrever o fenômeno na
sua totalidade. O que se tem são informações
experimentais que mostram o aumento do valor do
coeficiente de difusão para altos valores de
normalidade.

28. Correlação de Gordon
(usada para estimar o coeficiente de difusão)
Correlação de Agar/Hartley e Crank