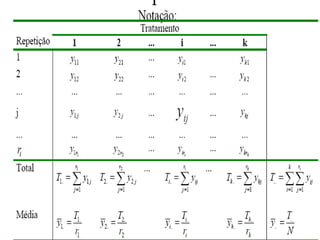
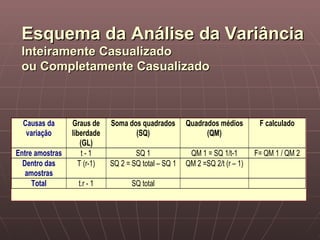
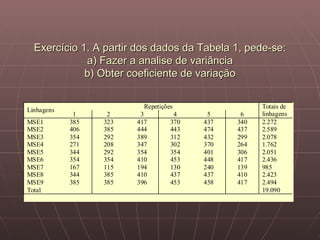
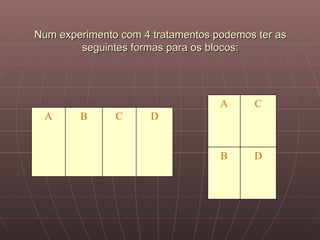
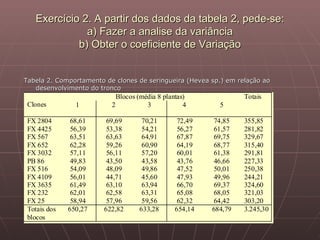
O documento discute os princípios básicos do planejamento de experimentos e delineamentos estatísticos, incluindo a identificação de unidades experimentais, fatores, tratamentos e variáveis-resposta, e a importância da aleatorização. Ele também descreve delineamentos completamente aleatórios e em blocos casualizados.