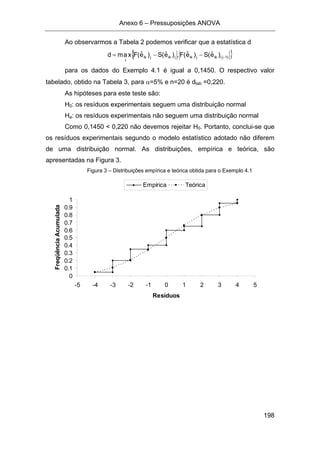
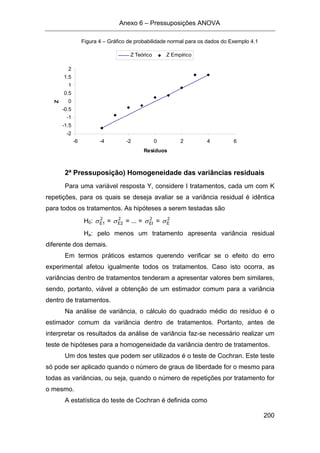
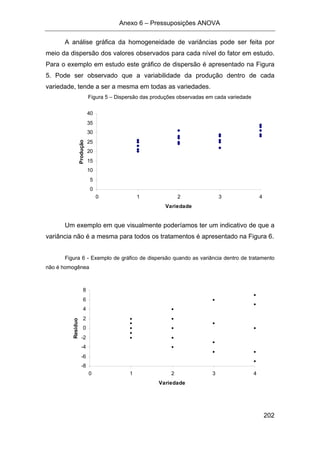
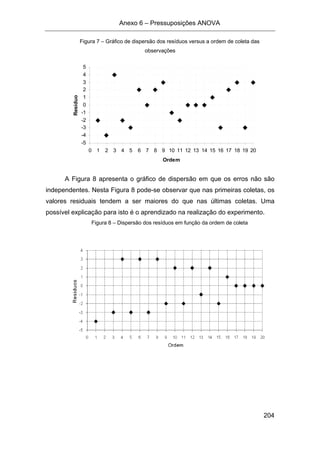
1. O documento apresenta informações sobre o curso de Estatística Experimental (EST 220) ministrado na Universidade Federal de Viçosa no primeiro período de 2010, incluindo conteúdo programático, sistema de avaliação, monitoria e bibliografia de apoio.
2. Serão aplicadas três provas igualmente ponderadas ao longo do semestre para avaliação dos estudantes, além de uma prova substitutiva. O conteúdo cobrado em cada prova será informado com antecedência.
3. O curso abordará temas como testes


































![EST 220 – Estatística Experimental – I/2008
____________________________________________________________________
38
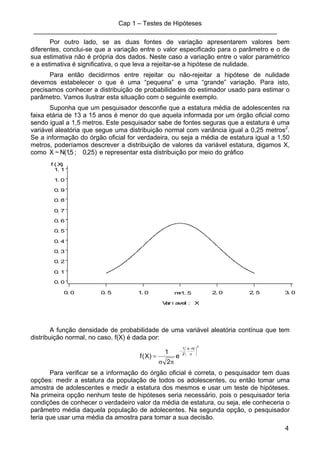
em que,
ijY é o valor observado para a variável resposta obtido para o i-ésimo tratamento
em sua j-ésima repetição;
m média de todos os valores possíveis da variável resposta;
it é o efeito do tratamento i no valor observado ijY ;
mmt ii −=
ije é o erro experimental associado ao valor observado ijY ;
iijij mYe −=
O erro experimental ocorre em todos os experimentos, porque não é possível
controlar o efeito de fontes de variações que ocorrem de forma aleatória e desconhecida.
Este erro é o responsável pela variação observada entre as observações obtidas nas
repetições para cada tratamento.
4.4. Análise de Variância
É uma técnica de análise estatística que permite decompor a variação total, ou
seja, a variação existente entre todas as observações, na variação devido à diferença
entre os efeitos dos tratamentos e na variação devido ao acaso, que também é
denominada de erro experimental ou resíduo.
No entanto, para que esta técnica seja empregada é necessário que sejam
satisfeitas as seguintes pressuposições:
1a
) os efeitos do modelo estatístico devem ser aditivos;
2a
) os erros experimentais devem ser normalmente distribuídos, independentes, com
média zero e com variância comum.
Partindo do modelo estatístico, pode-se decompor a variação entre os valores
observados nas diferentes causas de variabilidade, como demonstrado a seguir:
Considere o modelo estatístico para um experimento instalado segundo o DIC:
ijiij etmY ++=
fazendo mmt ii −= e eij = Yij – mi , tem-se:
( ) ( )iijiij mYmmmY −+−=− ,
substituindo iji eem,m por seus estimadores tem-se:
( ) ( )iijiij mˆYmˆmˆmˆY −+−=− ,
elevando ambos os membros ao quadrado
( ) ( ) ( )[ ]2
iiji
2
ij mˆYmˆmˆmˆY −+−=− ,
aplicando somatório
( ) ( ) ( )[ ]∑∑ ====
−+−=−
J,I
1j,1i
2
iiji
J,I
1j,1i
2
ij mˆYmˆmˆmˆY ,
( ) ( ) ( ) ∑∑∑∑ ========
+−+−=−
J,I
1j,1i
J,I
1j,1i
2
iij
J,I
1j,1i
2
i
J,I
1j,1i
2
ij produtosduplosmˆYmˆmˆmˆY
pode-se verificar que: 0produtosduplos
J,I
1j,1i
=∑==
.
Escrevendo de uma forma mais simplificada a igualdade anterior temos:
SQTotal = SQTrat + SQRes
Por meio das fórmulas obtidas anteriormente, pode-se obter os valores para as
respectivas somas de quadrados. No entanto, essas fórmulas demandam muitos cálculos.](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-43-320.jpg)


![EST 220 – Estatística Experimental – I/2008
____________________________________________________________________
41
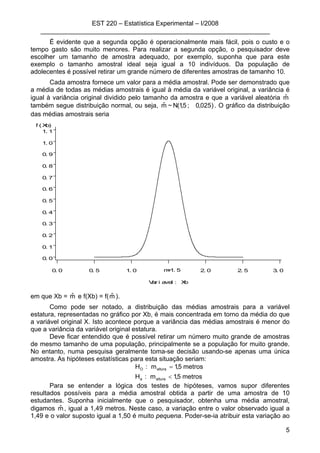
FV GL SQ QM F Ftab; α
Tratamentos (I-1) SQTrat
1I
SQTrat
− sReQM
QMTrat
[(I-1); I(J-1)]
Resíduo I(J-1) SQRes
( )1JI
sReSQ
−
Total IJ - 1 SQTotal
A partir das SQTrat e SQRes, obtém-se os respectivos quadrados médios, por
meio do quociente entre a soma de quadrados com o respectivo número de graus de
liberdade.
Para se concluir se existe diferença entre tratamentos, calcula-se o valor de F, que
é obtido pelo quociente do QMTrat com o QMRes. Este valor de F calculado deve ser
comparado com o valor de F tabelado, o qual é obtido na tabela de distribuição da
variável aleatória F, de acordo com o nível de significância do teste, graus de liberdade
para tratamentos e graus de liberdade para resíduo.
As hipóteses para o teste F da análise de variância para tratamentos são as
seguintes:
mm...mm:H I210 ==== , o que equivale a dizer que todos os possíveis contrastes
entre as médias dos tratamentos, são estatisticamente nulos, ao nível de
probabilidade que foi executado o teste.
0a Hnão:H , o que equivale a dizer que existe pelo menos um contraste entre as médias
dos tratamentos, estatisticamente diferentes de zero, ao nível de probabilidade que foi
realizado o teste.
A regra decisória para o teste F é a seguinte:
- se o valor do F calculado for maior ou igual ao valor do F tabelado, então rejeita-se
0H e conclui-se que os tratamentos tem efeito diferenciado ao nível de significância
em que foi realizado o teste;
- se o valor de F calculado for menor que o valor do F tabelado, então não rejeita-se
0H e conclui-se que os tratamentos têm efeitos iguais ao nível de significância em
que foi realizado o teste.
4.5. Coeficiente de Variação
O coeficiente de variação é calculado da seguinte maneira:
100
mˆ
sReQM
CV ⋅=
O CV é utilizado para avaliação da precisão de experimentos. Quanto menor o CV
mais preciso tende a ser o experimento. A título de classificação geral pode-se utilizar a
seguinte tabela
C.V. Avaliação Precisão
< 10% Baixo Alta
10 a 20% Médio Média
20 a 30% Alto Baixa
>30% Muito Alto Muito Baixa
Porém o valor do CV não tem nada de absoluto, pois existe uma variabilidade
inerente a cada área de pesquisa. Por exemplo, experimentos realizados em locais com](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-46-320.jpg)













![Cap 6 – Delineamento em Blocos Casualizados
_____________________________________________________________________
55
m média de todas as unidades experimentais para a variável em estudo.
it é o efeito do particular tratamento i no valor observado ijY :
mmt ii −=
jb é o efeito do bloco j no valor observado ijY :
mmb jj −=
ije é o erro associado a observação ijY :
jiijij mmmYe −−+=
6.4. Análise de Variância
Para realizar a análise dos dados obtidos de um experimento instalado segundo o
DBC, deve-se decompor a variação total que existe entre todas as observações nas
partes que a compõe. Neste tipo de delineamento, a decomposição é feita da seguinte
forma:
SQTotal = SQTratamentos + SQBlocos + SQResíduo
conforme é demonstrado a seguir.
Considere o modelo estatístico para um experimento instalado segundo o DBC:
ijjiij ebtmY +++=
fazendo mmt ii −= e mmb jj −= , tem-se:
( ) ( ) ijjiij emmmmmY +−+−=− ,
substituindo ijji eem,mm por seus estimadores tem-se:
( ) ( ) ijjiij eˆmˆmˆmˆmˆmˆY +−+−=− ,
elevando ambos os membros ao quadrado
( ) ( ) ( )[ ]2
ijji
2
ij eˆmˆmˆmˆmˆmˆY +−+−=− ,
aplicando somatório
( ) ( ) ( )[ ]∑∑ ====
+−+−=−
J,I
1j,1i
2
ijji
J,I
1j,1i
2
ij eˆmˆmˆmˆmˆmˆY ,
( ) ( ) ( ) ∑∑∑∑∑ ==========
++−+−=−
J,I
1j,1i
J,I
1j,1i
2
ij
J,I
1j,1i
2
j
J,I
1j,1i
2
i
J,I
1j,1i
2
ij produtosduploseˆmˆmˆmˆmˆmˆY
Ou seja:
SQTotal = SQTratamentos + SQBlocos + SQResíduo + ∑==
J,I
1j,1i
produtosduplos
pode-se verificar que: 0produtosduplos
J,I
1j,1i
=∑==
.
Por meio das fórmulas obtidas no desenvolvimento anterior, pode-se obter os
valores para as respectivas somas de quadrados. No entanto, essas fórmulas são muito
trabalhosas para se obter tais valores.
São fornecidas a seguir, fórmulas mais práticas para se obter as somas de
quadrados.](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-60-320.jpg)


















![EST 220 – Estatística Experimental – I/2008
___________________________________________________________
74
8.4. Modelo estatístico
Considere um experimento fatorial, com dois fatores: o fator A com I
níveis e o fator B com J níveis, instalados segundo o DIC, com K repetições. O
modelo estatístico para um experimento como este é:
( ) ijkijjiijk emY +αβ+β+α+=
em que,
ijkY é o valor observado para a variável em estudo referente a k-ésima
repetição da combinação do i-ésimo nível do fator A com o j-ésimo
nível do fator B;
m é a média de todas as unidades experimentais para a variável em
estudo;
iα é o efeito do i-ésimo nível do fator A no valor observado ijkY ;
jβ é o efeito do j-ésimo nível do fator B no valor observado ijkY ;
( )ijαβ é o efeito da interação do i-ésimo nível do fator A com o j-ésimo nível
do fator B;
ijke é o erro associado a observação ijkY .
Para um experimento fatorial instalado segundo o DBC, com K blocos, o
modelo estatístico seria:
( ) ijk
e
kijji
m
ijk
Y +ω+αβ+β+α+=
em que,
kω é o efeito do k-ésimo bloco na observação ijkY .
8.5. Análise de Variância
A análise de variância de um experimento fatorial é feita desdobrando-se a
soma de quadrados de tratamentos nas partes devido aos efeitos principais de
cada fator e na parte devido à interação entre os fatores.
O quadro a seguir apresenta como seria a análise de um experimento
fatorial, com 2 fatores A e B, com I e J níveis, respectivamente, e K repetições,
instalado segundo o DIC.
FV GL SQ QM F Ftab;α
A (I-1) SQA - - -
B (J-1) SQB - - -
AxB (I-1)(J-1) SQAxB
( )( )1J1I
SQAxB
−− sReQM
QMAxB
[(I-1)(J-1); n2]
(Trat) (IJ-1) (SQTrat) - - -
Resíduo n2=IJ(K-1) SQRes
( )1KIJ
sReSQ
−
- -
Total IJK – 1 SQTotal - -
As fórmulas para a obtenção das somas de quadrados são as seguintes:](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-79-320.jpg)
![Cap 8 – Experimentos Fatoriais
____________________________________________________________
75
CYSQTotal
K,J,I
1k,1j,1i
2
ijk −= ∑===
IJK
Y
C
2
K,J,I
1k,1j,1i
ijk ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∑===
C
K
Y
SQTrat
J,I
1j,1i
2
.ij
−= ∑==
C
JK
A
SQA
I
1i
2
i
−= ∑=
C
IK
B
SQB
J
1j
2
j
−= ∑=
SQAxB = SQTrat – SQA – SQB
SQResíduo = SQTotal – SQTrat
O quadro abaixo apresenta como seria a análise de um experimento
fatorial, com 2 fatores A e B, com I e J níveis, respectivamente, e K repetições
(ou blocos), instalado segundo o DBC.
FV GL SQ QM F Ftab,α
A (I-1) SQA - - -
B (J-1) SQB - - -
AxB (I-1)(J-1) SQAxB
( )( )1J1I
SQAxB
−− sReQM
QMAxB
[(I-1)(J-1); n2]
(Trat) (IJ-1) (SQTrat) - - -
Blocos K-1 SQBlocos - - -
Resíduo n2=(IJ-1)(K-1) SQRes
( )1K)1IJ(
sReSQ
−−
- -
Total IJK - 1 SQTotal - - -
Nesta situação,
C
IJ
W
cosSQBlo
K
1k
2
k
−= ∑=
em que,
Total do k-ésimo bloco: k
J,I
1j,1i
ijkk YYW ••== ∑==
Conforme apresentado nas duas tabelas anteriores, na análise dos dados
oriundos de um experimento fatorial, para os dois tipos de delineamentos,
deve-se inicialmente proceder ao teste F para a interação entre os fatores. As
hipóteses para o teste F da interação são:
:H0 Os fatores A e B atuam independentemente sobre a variável
resposta em estudo.
:Ha Os fatores A e B não atuam independentemente sobre a variável
resposta em estudo.
O resultado deste teste F para a interação indica como as comparações dos
níveis de um fator devem ser realizadas. Temos dois resultados possíveis para
o teste F da interação os quais serão apresentados a seguir.](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-80-320.jpg)
![EST 220 – Estatística Experimental – I/2008
___________________________________________________________
76
8.5.1 Interação não-significativa
Este caso ocorre quando a hipótese 0H para a interação entre os fatores
não é rejeitada. Este resultado implica que os efeitos dos fatores atuam de
forma independente.
Portanto recomenda-se que as comparações dos níveis de um fator
sejam feitas de forma geral em relação ao outro fator, ou seja, independente
dos níveis outro fator. O passo seguinte na análise estatística dos dados
experimentais é proceder ao teste F para cada fator como ilustrado na tabela
apresentada a seguir para o caso do DBC.
FV GL SQ QM F Ftab, α
A (I-1) SQA
( )1I
SQA
− sReQM
QMA
[(I-1);n2]
B (J-1) SQB
( )1J
SQB
− sReQM
QMB
[(J-1);n2]
AxB (I-1)(J-1) SQAxB
( )( )1J1I
SQAxB
−−
não-
siginificativo
-
(Trat) (IJ-1) (SQTrat) - - -
Blocos K-1 SQBlocos - - -
Resíduo n2=(IJ-1)(K-1) SQRes
( )1K)1IJ(
sReSQ
−−
- -
Total IJK - 1 SQTotal - - -
As hipóteses para realizar o teste F para os efeitos principais são
Fator A
AI2A1A0 m...mm:H === ou seja, todos os possíveis contrastes entre as médias
dos níveis do fator A, são estatisticamente nulos, ao nível de probabilidade
em que foi executado o teste.
0a Hnão:H ou seja, existe pelo menos um contraste entre as médias dos
níveis do fator A, que é estatisticamente diferente de zero, ao nível de
probabilidade em que foi executado o teste.
Fator B
BJ2B1B0 m...mm:H === ou seja, todos os possíveis contrastes entre as médias
dos níveis do fator B, são estatisticamente nulos, ao nível de probabilidade
em que foi executado o teste.
0a Hnão:H ou seja, existe pelo menos um contraste entre as médias dos
níveis do fator B, que é estatisticamente diferente de zero, ao nível de
probabilidade em que foi executado o teste.
Se os fatores A e B forem qualitativos, e o teste F para A e/ou B, for não
significativo, a aplicação do teste de médias é desnecessária. Se o teste F for
significativo, para A e/ou B, aplica-se um teste de médias para comparar os
níveis do fator. As estimativas das médias dos níveis dos fatores são obtidas
por](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-81-320.jpg)

![EST 220 – Estatística Experimental – I/2008
___________________________________________________________
78
Para a aplicação do teste Scheffé para testar os contrastes YA e YB temos
que usar
S Ftab
A ∑=
−=
I
1i
2
itab a
JK
sReQM
F)1I(S Fα [(I -1); n2]
B ∑=
−=
J
1j
2
jtab b
IK
sReQM
F)1J(S Fα [(J -1); n2]
As hipóteses para os testes de Scheffé e t para testar os contrastes são
Fator A → H0 : CA = 0 versus Ha : CA ≠ 0
Fator B → H0 : CB = 0 versus Ha : CB ≠ 0
8.5.2 Interação significativa
Este caso ocorre quando a hipótese H0 para a interação entre os fatores
é rejeitada. Este resultado implica que os efeitos dos fatores atuam de forma
dependente. Neste caso as comparações entre os níveis de um fator levam em
consideração o nível do outro fator, pois o resultado significativo para a
interação indica que o efeito de um fator depende do nível do outro fator.
Portanto, não é recomendado realizar o teste F para cada fator
isoladamente tal como foi apresentado para o caso da interação não-
significativa. O procedimento recomendado é realizar o desdobramento do
efeito da interação.
Para realizar este desdobramento deve-se fazer uma nova análise de
variância em que os níveis de um fator são comparados dentro de cada nível
do outro fator, tal como apresentado nas tabelas a seguir.
Desdobramento para comparar os níveis de A dentro de cada nível de B,
ou seja, estudar A/B
FV GL SQ QM F Ftab, α
A/B1 (I-1) SQA/B1
( )1I
1B/SQA
− sReQM
1B/QMA
[(I-1);n2]
A/B2 (I-1) SQA/B2
( )1I
2B/SQA
− sReQM
2B/QMA
[(I-1);n2]
... ... ... ... ... ...
A/BJ (I-1) SQA/BJ
( )1I
BJ/SQA
− sReQM
BJ/QMA
[(I-1);n2]
Resíduo n2 QMRes -
Total IJK - 1 SQTotal - - -
As hipóteses para testar as fontes de variação da tabela acima, para j=1,
2, 3, ..., J, são
H0 : mA1/Bj = mA2/Bj = ... = mAI/Bj
0a Hnão:H
Desdobramento para comparar os níveis de B dentro de cada nível de A,
ou seja estudar B/A](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-83-320.jpg)
![Cap 8 – Experimentos Fatoriais
____________________________________________________________
79
FV GL SQ QM F Ftab, α
B/A1 (J-1) SQB/A1
( )1J
1A/SQB
− sReQM
1A/QMB
[(J-1);n2]
B/A2 (J-1) SQB/A2
( )1J
2A/SQB
− sReQM
2A/QMB
[(J-1);n2]
... ... ... ... ... ...
B/AI (J-1) SQB/AI
( )1J
AI/SQB
− sReQM
AI/QMB
[(J-1);n2]
Resíduo n2 QMRes -
Total IJK - 1 SQTotal - - -
As hipóteses para testar as fontes de variação da tabela acima, para i=1,
2, 3, ..., I, são
H0 : mB1/Ai = mB2/Ai = ... = mBJ/Ai
0a Hnão:H
Em que as SQA/Bj e SQB/Ai podem ser obtidas usando a fórmula geral
para a soma de quadrados dada por
∑
∑
∑
=
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−= k
1i
i
2
k
1i
ik
1i i
2
i
r
X
r
X
SQ
Se os fatores forem qualitativos, procede-se ao teste F para cada fonte de
variação do desdobramento. Nas fontes de variação em que o teste F foi
significativo e o fator tem mais de dois níveis, recomenda-se a aplicação de um
teste de médias. As estimativas das médias dos níveis dos fatores são obtidas
por
Fator A →
K
A
mˆ i
Ai =
Fator B →
K
B
mˆ j
Bj =
Para realizar o teste de Tukey para comparar as médias dos níveis dos
fatores em teste temos que usar
∆ qα
A
K
sReQM
q (I;n2)
B
K
sReQM
q (J;n2)](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-84-320.jpg)
![EST 220 – Estatística Experimental – I/2008
___________________________________________________________
80
Para o teste de Duncan temos que usar
Di zα
A
K
sReQM
iz (nA;n2)
B
K
sReQM
iz (nB;n2)
Em que nA e nB são os números de médias ordenadas abrangidas pelo
contraste sendo testados.
As hipóteses para os testes Tukey e Duncan para comparar as médias dos
níveis dos fatores são
Fator A → H0 : mAi/Bj = mAu/Bj versus Ha : mAi/Bj ≠ mAu/Bj para i ≠ u = 1, 2, 3, ...
, I e j = 1, 2, ... , J
Fator B → H0 : mBj/Ai = mBu/Ai versus Ha : mBj/Ai ≠ mBu/Ai para j ≠ u = 1, 2, 3, ...
, J e i = 1, 2, ... , I
Para a aplicação do teste t temos que usar
t ttab
A
∑=
−
I
1i
2
i
AA
a
K
sReQM
CCˆ
tα (n2)
B
∑=
−
JI
1j
2
i
BB
b
K
sReQM
CCˆ
tα (n2)
Em que
CA = a1mA1/Bj + a2mA2/Bj + ... + aImAI/Bj para j = 1, 2, ..., J e
CB = b1mB1/Ai + b2mB2/Ai + ... + bJmBJ/Ai para i = 1, 2, ... , I
Para a aplicação do teste Scheffé para testar os contrastes CA e CB temos
que usar
S Ftab
A ∑=
−=
I
1i
2
itab a
K
sReQM
F)1I(S Fα [(I -1); n2]
B ∑=
−=
J
1j
2
jtab b
K
sReQM
F)1J(S Fα [(J -1); n2]
As hipóteses para os testes de Scheffé e t para testar os contrastes são
Fator A → H0 : CA = 0 versus Ha : CA ≠ 0
Fator B → H0 : CB = 0 versus Ha : CB ≠ 0](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-85-320.jpg)















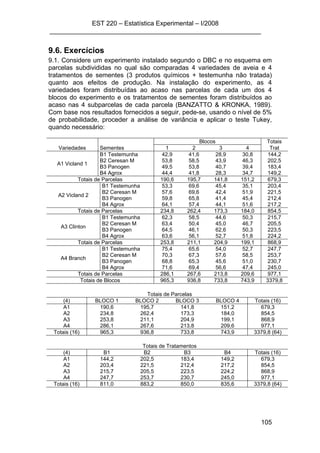
![Cap 9 – Experimentos em Parcelas Subdivididas
___________________________________________________________
98
FV GL SQ QM F Ftab; α
Blocos (K-1) SQBlocos - -
A (I-1) SQA
)1I(
SQA
−
-
Resíduo(a) (I-1)(K-1) SQRes(a)
)1K)(1I(
)a(síduoReSQ
−−
Parcelas IK-1 SQParcelas - -
B (J-1) SQB
)1J(
SQB
−
-
AxB (I-1)(J-1) SQAxB
)1J)(1I(
SQAxB
−− )b(sReQM
QMAxB [(I-1)(J-1); n2]
Resíduo(b) n2 = I(J-1)(K-1) SQRes(b)
)1K)(1J(I
)b(síduoReSQ
−−
-
Total IJ K- 1 SQTotal - -
em que:
CYSQTotal
K,J,I
1k,1j,1i
2
ijk −= ∑===
IJK
Y
C
K,J,I
1k,1j,1i
ijk ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∑===
C
IJ
W
cosSQBlo
K
1K
2
K
−= ∑=
C
J
P
SQParcelas
Z
1z
2
z
−=
∑=
C
K
Y
SQTrat
J,I
1j,1i
2
.ij
−= ∑==
C
JK
A
SQA
I
1i
2
I
−= ∑=
C
IK
B
SQB
J
1j
2
J
−= ∑=
SQAxB = SQTrat – SQA – SQB
SQRes(a) = SQParcelas - SQBlocos - SQA
SQRes(b) = SQTotal - SQParcelas - SQB - SQAxB
Tal como no esquema fatorial, na análise dos dados oriundos de um
experimento em parcelas subdivididas deve-se inicialmente proceder ao teste
F para a interação entre os fatores. As hipóteses para o teste F da interação
são:
:H0 Os fatores A e B atuam independentemente sobre a variável
resposta em estudo.
:Ha Os fatores A e B não atuam independentemente sobre a variável
resposta em estudo.
O resultado deste teste F para a interação indica como as
comparações dos níveis de um fator devem ser realizadas. Temos dois
resultados possíveis para o teste F da interação os quais serão apresentados
a seguir.](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-103-320.jpg)
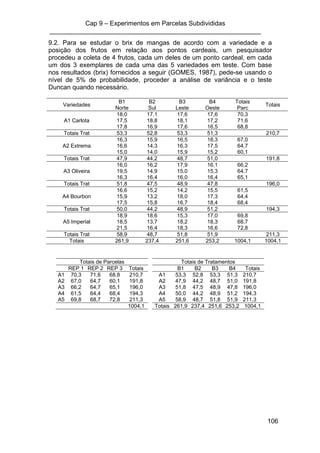
![EST 220 – Estatística Experimental – I/2008
___________________________________________________________
99
9.4.1 Interação não-significativa
Este caso ocorre quando a hipótese H0 para a interação entre os
fatores não é rejeitada. Este resultado implica que os efeitos dos fatores
atuam de forma independente.
Portanto recomenda-se que as comparações dos níveis de um fator
sejam feitas de forma geral em relação ao outro fator, ou seja, independente
dos níveis outro fator. O passo seguinte na análise estatística dos dados
experimentais é proceder ao teste F para cada fator como ilustrado na tabela
apresentada a seguir para o caso do DBC.
FV GL SQ QM F Ftab; α
Blocos (K-1) SQBlocos - -
A (I-1) SQA
)1I(
SQA
− )a(sReQM
QMA
[(I-1); n2]
Resíduo(a) n2 = (I-1)(K-1) SQRes(a)
)1K)(1I(
)a(sReSQ
−−
-
Parcelas IK-1 SQParcelas - -
B (J-1) SQB
)1J(
SQB
− )b(sReQM
QMB
[(J-1); n3]
AxB (I-1)(J-1) SQAxB
)1J)(1I(
SQAxB
−−
não-signficativo -
Resíduo(b) n3 = I(J-1)(K-1) SQRes(b)
)1K)(1J(I
)b(sReSQ
−−
-
Total IJ K- 1 SQTotal - -
As hipóteses para realizar o teste F para os efeitos principais são
Fator A
AI2A1A0 m...mm:H === ou seja, todos os possíveis contrastes entre as
médias dos níveis do fator A, são estatisticamente nulos, ao nível de
probabilidade em que foi executado o teste.
0a Hnão:H ou seja, existe pelo menos um contraste entre as médias dos
níveis do fator A, que é estatisticamente diferente de zero, ao nível de
probabilidade em que foi executado o teste.
Fator B
BJ2B1B0 m...mm:H === ou seja, todos os possíveis contrastes entre as
médias dos níveis do fator B, são estatisticamente nulos, ao nível de
probabilidade em que foi executado o teste.
0a Hnão:H ou seja, existe pelo menos um contraste entre as médias dos
níveis do fator B, que é estatisticamente diferente de zero, ao nível de
probabilidade em que foi executado o teste.
Se os fatores A e B forem qualitativos, e o teste F para A e/ou B, for não
significativo, a aplicação do teste de médias é desnecessária. Se o teste F for
significativo, para A e/ou B, aplica-se um teste de médias para comparar os](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-104-320.jpg)

![EST 220 – Estatística Experimental – I/2008
___________________________________________________________
101
Para a aplicação do teste Scheffé para testar os contrastes CA e CB temos
que usar
S Ftab
A ∑=
−=
I
1i
2
itab a
JK
)a(sReQM
F)1I(S Fα [(I -1); n2]
B ∑=
−=
J
1j
2
itab b
IK
)b(sReQM
F)1J(S Fα [(J -1); n3]
As hipóteses para os testes de Scheffé e t para testar os contrastes são
Fator A → H0 : CA = 0 versus Ha : CA ≠ 0
Fator B → H0 : CB = 0 versus Ha : CB ≠ 0
9.4.2 Interação significativa
Este caso ocorre quando a hipótese H0 para a interação entre os
fatores é rejeitada. Este resultado implica que os efeitos dos fatores atuam de
forma dependente. Neste caso as comparações entre os níveis de um fator
levem em consideração o nível do outro fator, pois o resultado significativo
para a interação indica que o efeito de um fator depende do nível do outro
fator.
Portanto, não é recomendado realizar o teste F para cada fator
isoladamente tal como foi apresentado para o caso da interação não-
significativa. O procedimento recomendado é realizar o desdobramento do
efeito da interação.
Para realizar este desdobramento deve-se fazer uma nova análise de
variância em que os níveis de um fator são comparados dentro de cada nível
do outro fator, tal como apresentado nas tabelas a seguir.
Para comparar os níveis de um fator principal em cada nível do fator
secundário, é necessário fazer uma combinação das duas estimativas obtidas
para o erro experimental bem como do número de graus de liberdade
associado as mesmas. Esta combinação é denominada de resíduo
combinado (ResComb). A estimativa do quadrado médio deste resíduo
combinado é obtida por
( )
J
)b(sReQM1J)a(sReQM
CombsReQM
−+
=
O número de graus de liberdade associado a esta estimativa é obtido
pela fórmula dos graus de liberdade de Satterhwaitte (n*) dada por
( ) ( ) ( )[ ]
( )[ ]
( )
( ) ( )[ ]
( )bsRe.l.g
bsReQM1J
asRe.l.g
asReQM
bsReQM1JasReQM
*n 22
2
−
+
−+
=
Desdobramento para comparar os níveis de A dentro de cada nível de
B, ou seja estudar A/B](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-106-320.jpg)
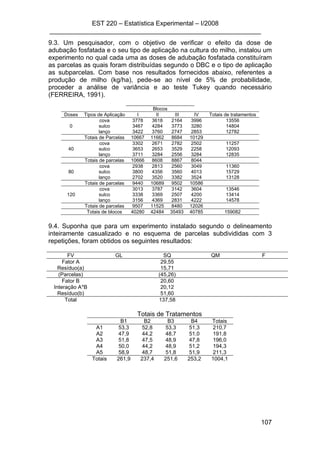
![Cap 9 – Experimentos em Parcelas Subdivididas
___________________________________________________________
102
FV GL SQ QM F Ftab, α
A/B1 (I-1) SQA/B1
( )1I
1B/SQA
− sCombReQM
1B/QMA
[(I-1);n*]
A/B2 (I-1) SQA/B2
( )1I
2B/SQA
− sCombReQM
2B/QMA
[(I-1);n*]
... ... ... ... ... ...
A/BJ (I-1) SQA/BJ
( )1I
BJ/SQA
− sCombReQM
BJ/QMA
[(I-1);n*]
ResCom
b
n*
QMResCom
b
-
Total IJK - 1 SQTotal - - -
As hipóteses para testar as fontes de variação da tabela acima, para
j=1, 2, 3, ..., J, são
H0 : mA1/Bj = mA2/Bj = ... = mAI/Bj
0a Hnão:H
Desdobramento para comparar os níveis de B dentro de cada nível de
A, ou seja estudar B/A
FV GL SQ QM F Ftab, α
B/A1 (J-1) SQB/A1
( )1J
1A/SQB
− )b(sReQM
1A/QMB
[(J-1);n3]
B/A2 (J-1) SQB/A2
( )1J
2A/SQB
− )b(sReQM
2A/QMB
[(J-1);n3]
... ... ... ... ... ...
B/AI (J-1) SQB/AI
( )1J
AI/SQB
− )b(sReQM
AI/QMB
[(J-1);n3]
Res(b
)
n3
QMRes(b
)
-
Total IJK - 1 SQTotal - - -
As hipóteses para testar as fontes de variação da tabela acima, para
i=1, 2, 3, ..., I, são
H0 : mB1/Ai = mB2/Ai = ... = mBJ/Ai
0a Hnão:H
Em que as SQA/Bj e SQB/Ai podem ser obtidas usando a fórmula
geral para a soma de quadrados dada por
∑
∑
∑
=
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−= k
1i
i
2
k
1i
ik
1i i
2
i
r
X
r
X
SQ
Se os fatores forem qualitativos, procede-se ao teste F para cada fonte
de variação do desdobramento. Nas fontes de variação em que o teste F foi
significativo e o fator tem mais de dois níveis, recomenda-se a aplicação de
um teste de médias. As estimativas das médias dos níveis dos fatores são
obtidas por](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-107-320.jpg)

![Cap 9 – Experimentos em Parcelas Subdivididas
___________________________________________________________
104
CA = a1mA1/Bj + a2mA2/Bj + ... + aImAI/Bj para j = 1, 2, ..., J e
CB = b1mB1/Ai + b2mB2/Ai + ... + bjmBJ/Ai para i = 1, 2, ... , I
Para a aplicação do teste Scheffé para testar os contrastes CA e CB temos
que usar
S Ftab
A ∑=
−=
I
1i
2
itab a
K
sCombReQM
F)1I(S Fα [(I -1); n*
]
B ∑=
−=
J
1j
2
jtab b
K
)b(sReQM
F)1J(S Fα [(J -1); n3]
As hipóteses para os testes de Scheffé e t para testar os contrastes são
Fator A → H0 : CA = 0 versus Ha : CA ≠ 0
Fator B → H0 : CB = 0 versus Ha : CB ≠ 0
9.5. Vantagens e desvantagens
Em comparação com experimentos fatoriais, experimentos em
parcelas subdivididas são mais fáceis de instalar. No entanto, existe duas
estimativas de variância residual: uma associada às parcelas e outra
associada às subparcelas. Este desdobramento da variância residual faz com
que o número de graus de liberdade associado a cada um dos resíduos seja
menor do o associado ao resíduo se o experimento tivesse sido instalado
segundo o esquema fatorial.
Conseqüentemente, há uma tendência de se obter maior valor para a
estimativa do erro experimental. Portanto, em experimentos com parcelas
subdivididas, todos os efeitos são avaliados com menor precisão que nos
experimentos fatoriais correspondentes. Por isso, sempre que possível, é
preferível utilizar experimentos fatoriais em lugar dos experimentos em
parcelas subdivididas.](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-109-320.jpg)




![Cap 10 – Regressão
____________________________________________________________________
112
distâncias entre os pontos do diagrama e os respectivos pontos na curva da equação
estimada é minimizada, obtendo-se, desta forma, uma relação funcional entre X e Y, para
o modelo escolhido, com um mínimo de erro possível.
10.3.1. Modelo linear de 1º grau
O modelo estatístico para esta situação seria:
ii10i eXY +β+β=
em que
iY é o valor observado para a variável dependente Y no i-ésimo nível da variável
independente X;
0β é a constante de regressão. Representa o intercepto da reta com o eixo dos Y;
1β é o coeficiente de regressão. Representa a variação de Y em função da variação
de uma unidade da variável X;
iX é o i-ésimo nível da variável independente X ( )n,,2,1i K= ; e
ie é o erro que está associado à distância entre o valor observado Yi e o
correspondente ponto na curva, do modelo proposto, para o mesmo nível i de X.
Para se obter a equação estimada, vamos utilizar o MMQ, visando a minimização
dos erros. Assim, tem-se que:
i10ii XYe β−β−=
elevando ambos os membros da equação ao quadrado,
[ ]2
i10i
2
i XYe β−β−=
aplicando o somatório,
[ ]∑∑ ==
β−β−=
n
1i
2
i10i
n
1i
2
i XYe (1)
Por meio da obtenção de estimadores de 10 e ββ , que minimizem o valor obtido na
expressão anterior, é possível alcançar a minimização da soma de quadrados dos erros.
Sabemos do Cálculo que para se encontrar o mínimo de uma equação deve-se
derivar a equação em relação à variável de interesse, e igualar a derivada resultante ao
valor zero. Portanto, derivando a expressão (1) em relação a 10 e ββ e igualando-as a
zero, obtém-se:
( )( ) ( )
( )( ) ( )( )⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
=β−β−⇒=−β−β−⇒=
∂β
∂
=β−β−⇒=−β−β−⇒=
∂β
∂
∑∑
∑
∑∑
∑
==
=
==
=
0XXˆˆY0XXˆˆY20
e
0XˆˆY01XˆˆY20
e
n
1i
ii10i
n
1i
ii10i
1
n
1i
2
i
n
1i
i10i
n
1i
i10i
0
n
1i
2
i
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=β−β−⇒=β−β−
=β−β−⇒=β−β−
∑∑∑∑∑∑
∑ ∑ ∑∑∑
======
= = ===
0XˆXˆXY0XˆXˆXY
0XˆˆnY0XˆˆY
n
1i
2
i1
n
1i
i0i
n
1i
i
2
i
n
1i
1i
n
1i
0i
n
1i
i
n
1i
n
1i
n
1i
i10
n
1i
ii10
n
1i
i](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-117-320.jpg)


![EST 220 – Estatística Experimental – I/2008
____________________________________________________________________
115
O valor de F da análise de variância, deve ser comparado, com o valor de F
tabelado ( )tabF , o qual se obtém na tabela da distribuição F de acordo com o nível de
significância do teste, e o número de graus de liberdade para a regressão e independente
da regressão, ou seja:
( )p1n;pFFtab −−= α .
A regra decisória para o teste F é:
- Se ⇒≥ tabFF Rejeita-se 0H ao nível de significância que foi realizado o teste. Pode-
se inferir que a variável independente influência significativamente a
variável dependente Y.
- Se ⇒< tabFF Não rejeita-se 0H ao nível de significância que foi realizado o teste.
Pode-se inferir que a variável independente não influência significativamente a
variável dependente Y.
10.4.2. Mais de um valor observado para cada nível da variável
independente
Nesta situação, existe mais de um valor observado para cada nível da variável
independente. Assim é possível obter uma estimativa da variância residual tal como
aquela obtida em modelos de delineamento, o que não é possível quando se tem uma
única observação para cada nível da variável independente.
Normalmente o que se faz numa situação como esta é inicialmente proceder a uma
análise de variância usual considerando o efeito do fator quantitativo como se fosse a
fonte de variação tratamentos numa análise de variância usual. Isto é realizado para que
se quantifique a variância residual. Posteriormente, o efeito de tratamentos é desdobrado
nos efeitos associado a um ajuste de um modelo de regressão e também a falta de ajuste
deste modelo. A escolha do modelo de regressão a ser ajustado é aquele que mais se
aproxima dos pontos médios observados para cada nível da variável independente. O
quadro abaixo resume o que acabou de ser descrito, para uma situação geral em que se
está testando I níveis da variável independente em um experimento instalado segundo o
delineamento inteiramente casualizado com K repetições. Pressupõe-se também que se
está testando um modelo de regressão com p coeficientes de regressão. O total de
observações neste experimento é igual a N=IK.
FV GL SQ QM F Ftab; α
Regressão p SQReg
p
gReSQ
sReQM
gReQM
[p; I(K – 1)]
Falta de Ajustamento I –1 – p SQFalta
1I
SQFalta
− sReQM
QMFalta
[I – 1 – p; I(K – 1)]
(Tratamentos) I – 1 SQTrat - -
Resíduo I(K – 1) SQRes
)1J(I
sReSQ
−
Total IK – 1 SQTotal - -
O teste F para a falta de ajustamento é realizado para verificar se o modelo
adotado está se ajustando bem aos dados. Se o teste F para a falta de ajustamento for
significativo, indica que o modelo ajustado não é apropriado e um novo modelo que se
ajuste melhor aos dados deve ser testado. Se por outro lado, a falta de ajustamento for
não-significativa indica que o modelo adotado se ajusta bem aos dados.
Conseqüentemente faz sentido analisar o teste F para a fonte de variação regressão para
saber se a variável independente tem influência significativa sobre a variável dependente.](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-120-320.jpg)



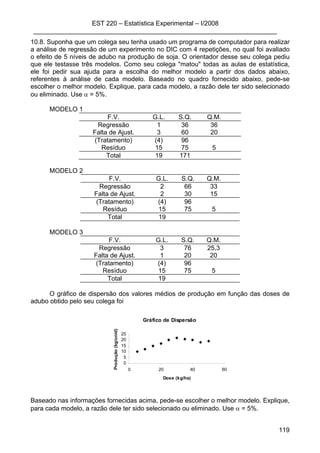






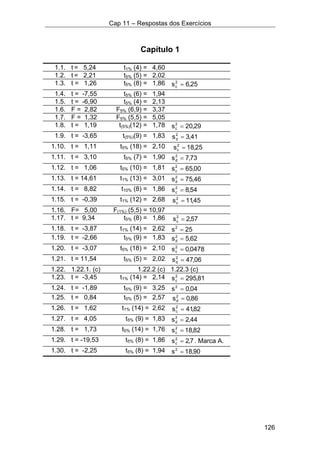

















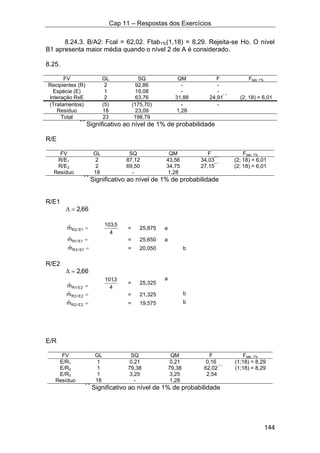







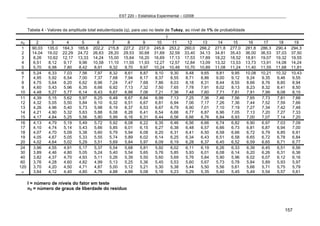
![Anexo 1 – Formulário e Tabelas
152
Formulário
n
x
mˆ
n
1i
i
i
∑=
=
GL
SQ
s2
= ∑
∑
∑
=
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−=
k
1i
k
1i
i
2
k
1i
i
i
2
i
r
X
r
X
SQ 2
ss = ( )
n
s
mˆs =
( ) ( )
2nn
s1ns1n
s
21
2
22
2
112
c
−+
−+−
= 2
2
s
s
F
<
>
=
n
s
mmˆ
t 0−
=
( ) ( )
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−−−
=
21
2
c
21
n
1
n
1
s
mm
2
mˆ
1
mˆ
t
n
s
mmˆ
t
2
D
DD −
=
n
d
mˆ
n
1i
i
D
∑=
=
1n
n
d
d
s
2
n
1i
in
1i
2
i
2
D
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
∑
∑ =
=
( )CˆVˆ
2
1
q=∆ ( )CˆVˆ
2
1
zD ii = ( )
2 2I I
2 i i
C
i 1 i 1i i
a aˆˆV C S QMRes
r r= =
= =∑ ∑
QMResíduo
q
K
∆ = i i
QMResíduo
D z
K
= ( ) ( )CˆVˆF1IS tab−=
( )CˆVˆ
Cˆ
t =
∑
∑
∑
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−= k
1i
i
2
k
1i
ik
1i i
2
i
r
X
r
X
SQ
mˆ
síduoReQM
100(%)CV =
i
i
i
r
T
mˆ =
N
G
mˆ =
( ) ( ) ( )[ ]
( )[ ]
( )
( ) ( )[ ]
( )bsRe.l.g
bsReQM1J
asRe.l.g
asReQM
bsReQM1JasReQM
*n 22
2
−
+
−+
=
( )
J
)b(sReQM1J)a(sReQM
CombsReQM
−+
=](https://image.slidesharecdn.com/apostiladeestatsticaexperimental-160415122731/85/Apostila-de-estatistica-experimental-157-320.jpg)