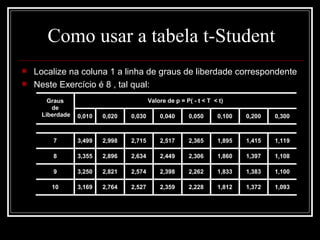
Este documento descreve como realizar um teste de hipóteses para comparar a média de uma variável em duas populações. Ele apresenta um exemplo detalhado onde se testa se o tempo médio de cirurgia cardíaca em pacientes diabéticos é maior do que em pacientes não diabéticos. O resumo da análise estatística realizada indica que a diferença encontrada não é estatisticamente significativa ao nível de 5%, portanto não pode-se afirmar que os diabéticos levam mais tempo.

1. Inferência Teste de Hipóteses Caso 1 - Uma Média Prof. Gercino Monteiro Filho

2. Teste de Média para uma Variável. Considere X uma variável pelo qual possua distribuição normal de média µ e variância σ 2 , ou seja: Considere agora uma amostra aleatória de X, seja X 1 , X 2 , X 3 , . . . , X 3 esta amostra, alem do mais, que esta amostra seja independente.

3. Teste de Média para uma Variável. Como X 1 , X 2 , X 3 , . . . , X n é uma amostra de X tem que: . . .

4. Teste de Média para uma Variável. Devido à Independência da Amostra, tem que: Ou seja a Média Amostral Possui Distribuição Normal de Paramétros:

5. Teste de Média para uma Variável. Nas condições descritas acima, pelo teorema de Normalidade do capitulo Conceitos, tem que o número:

6. Teste de Média para uma Variável. * Quadro de Hipótese * Neste caso existem as possibilidades:

7. Teste de Média para uma Variável. * Modelo Matemático de Análise * Neste caso utiliza o teorema descrito acima e o valor obtido é feito análise estatística, com o auxilio da Distribuição Probabilística t-Student.

8. Teste de Média para uma Variável. * Exemplo 1* Pesquisa: Avaliar o tempo de cirurgia em operações cardíacas em pacientes diabéticos. (Simulada) Uma amostra forneceu os valores: 249 – 267 – 298 – 304 – 268 – 264 – 239 – 273 – 267 e 255. Por pesquisas passadas sabe-se que pacientes não-diabéticos a média de duração é: 255,0 minutos, testar ao nível de 5,0% de significância se o tempo para realizar tal cirurgia em pacientes diabéticos é ou não superior ao de pacientes não-diabéticos.

9. * Exemplo 1 – Solução * Quadro de Hipóteses: Como o pleiteado é ser superior ou não é unilateral à direita, e assim: Onde μ é a duração média da cirurgia em pacientes diabéticos.

10. * Exemplo 1 – Estimativa * Da média: Da variância Do desvio Padrão

11. * Exemplo 1 – Analisando * Acreditando que tempo de cirurgia tenha distribuição normal (existe teste estatístico que o comprova), trata-se do teste t-student com uma amostra, e assim vem:

12. * Exemplo 1 – Modelo Matemático * Aqui: n = 9 (Tamanho da Amostra); Substituindo na fórmula vem:

13. Como usar a tabela t-Student Localize na coluna 1 a linha de graus de liberdade correspondente Neste Exercício é 8 , tal qual:

14. Como usar a tabela t-Student Localize o intervalo que contenha o valor especificado, neste caso: 1,8266 Olhando na tabela percebe que este número está entre: 1,860 e 1,397; Agora olha na linha de p e encontre o intervalo de p, nas linhas definidas por estes limites, 0,10 e 0,20

15. * Exemplo 1 – Conclusão * Com o uso da Tabela, obteve: Conclusão: Como p > 0,05 conclui que a diferença encontrada é não-significativa e sim casual portanto não pode afirmar que os diabéticos tem tempo de duração de cirurgia acima que dos pacientes normais.

16. Teste de Hipóteses Caso 1 – Uma Média FIM Prof. Gercino Monteiro