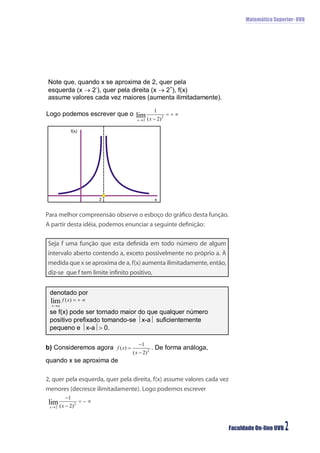
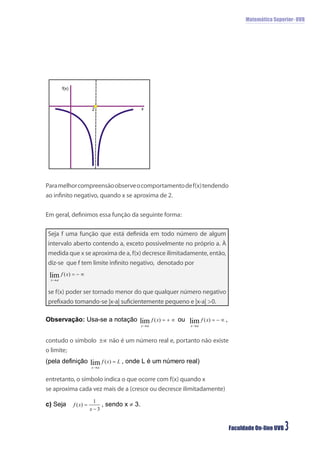
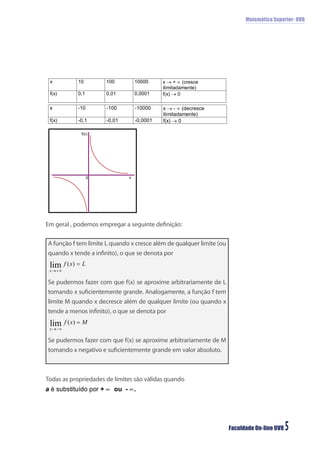
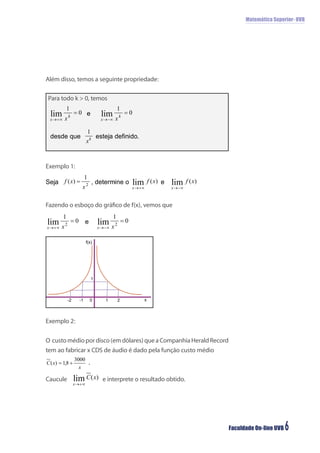
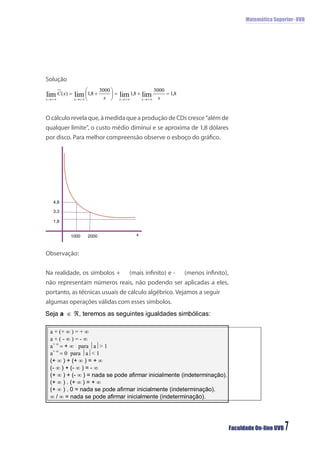
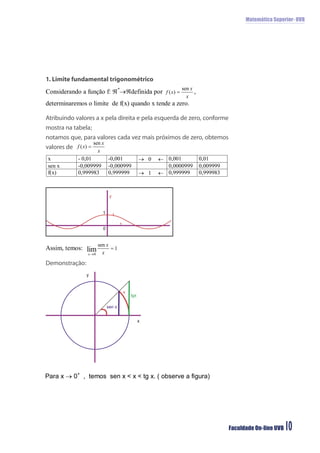
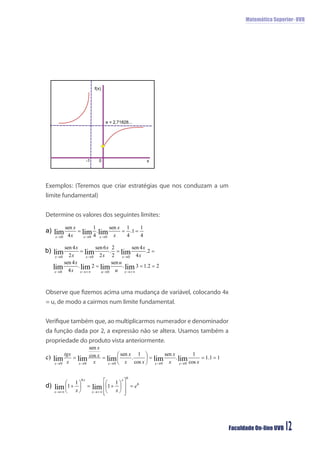
O documento discute limites infinitos e limites fundamentais em matemática superior. Aborda limites quando x se aproxima de um valor, limites quando x tende ao infinito ou menos infinito, e apresenta os limites fundamentais trigonométrico e exponencial.