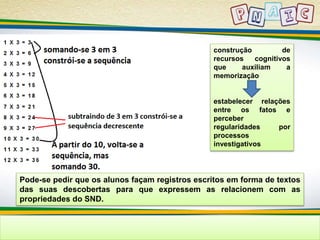
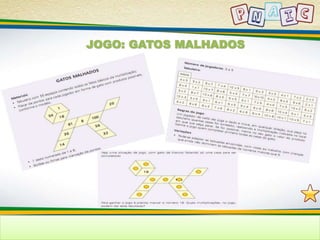
O documento discute estratégias para ensinar resolução de problemas matemáticos para crianças, incluindo abordagens como: 1) estimular estratégias individuais de resolução de problemas; 2) vivenciar situações matemáticas; e 3) socializar estratégias utilizadas. Também discute erros comuns de crianças em resolução de problemas e como superá-los, focando no significado conceitual em vez de apenas reprodução de procedimentos.

1. ORIENTADORA: ELAINE MARIA DA SILVA

2. PACTO –
UNIDADE 3 e 4
VAMOS BRINCAR DE CONSTRUIR AS
NOSSAS E OUTRAS HISTÓRIAS

3. LEITURA DELEITE
CHICO BENTO

4. Vocês conhecem o personagem Chico
Bento?
•De onde?
•Como podemos identificá-lo?
•Chico Bento se assemelha com algum
de nossos alunos?
•Por quê?

6. Qual o tipo de problema elaborado pela professora?
•Qual a diferença da forma como os enunciados da situação-problema
foram elaborados pelos personagens: Professora e Chico Bento?
Pergunta elaborada pela professora:
Chico, eu tinha 10 cabritos, vendi quatro, com quantos fiquei?
Pergunta elaborada por Chico:
Zé lelé, a fessora tinha 10 cabrito, vendeu quatro, quantos ficaram?
•Caso Zé lelé não questionasse Chico com a pergunta: Com ela ou com
quem comprou?, o problema teria como ser resolvido?
•Qual era o objetivo da professora com a atividade?
•Quais os sentidos que cada personagem atribuiu à palavra
PROBLEMA?
•Ao final do vídeo, a pergunta iniciada pela professora nos dá indícios
sobre o tipo de problema que iria ser solicitado?
•Chico, de fato, realizou um cálculo relacional?

7. Objetivos do Caderno 4
OPERAÇÕES NA RESOLUÇÃO
DE PROBLEMAS
 compreender os sentidos das operações de
adição, subtração, multiplicação e divisão,
integradas na resolução de problemas;
 elaborar, interpretar e resolver situações-problema
do campo aditivo (adição e
subtração) e multiplicativo (multiplicação e
divisão);

8. Objetivos do Caderno 4
 valorizar as estratégias pessoais e as
formas de representação espontâneas das
crianças, ampliando o repertório de
representações simbólicas;
 trabalhar com os algoritmos tradicionais
articulados a compreensão do Sistema de
Numeração Decimal
 uso de materiais manipulativos, jogos e
calculadora.

23. Atividade
 Analisar quais foram os erros e acertos de
cada forma de resolução e identificar quais
foram as dificuldades encontradas.

25. a) Como os alunos resolvem os problemas?
b) Quais alunos resolveram as contas
corretamente?
c) Qual a diferença entre conta e problema?

26. Qual a natureza dos erros? O
que se pode fazer para
superar as dificuldades dos
alunos?

27. ALGUMAS ESTRATÉGIAS DE CRIANÇAS
A CASA DO VOVÔ
VOVÔ DISSE QUE CRESCEU NUMA CASA ONDE HAVIA 12 PÉS E UM
RABO. QUEM PODERIA TER VIVIDO COM VOVÔ NESTA CASA?

28. VOVÔ DISSE QUE CRESCEU NUMA CASA ONDE HAVIA 12 PÉS E UM
RABO. QUEM PODERIA TER VIVIDO COM VOVÔ NESTA CASA?
“Na casa vivia o vovô, um
rinoceronte sem rabo e um
macaco com um rabo bem
grande e o neto do vovô
que está chorando porque
está com medo do
rinoceronte!”

29. “É o vovô, a vovó,
um filho chamado
Pedro e sua irmã
Laura e o cachorro
Totó. São 2 mais 2
que dá quatro,
mais 4 que dá 8 e
mais 4 pés do
cachorro que dá
12. O rabo é do
cachorro”.

30. “Na casa morava o vovô Carlos, a vovó Lu, seus netos
João e Bruna e um mostro enorme com quatro pernas e um
rabo!”

31. A: “Moravam seis
pessoas”.
P: E o rabo?
A: Aqui olha, o rabo
de cavalo da filha da
vovó.

32. A: Vovô, o neto,
um gato e rato!
P: Mas, não é só
um rabo?
A: É mesmo,
então vou
pensar numa
outra solução.

33. “O vovô, o
neto, o gato e
um rato sem
rabo. Porque o
gato comeu!”

34. “Um cachorro uma pessoa
e uma aranha.”

35. “Quatro pessoas e
um cachorro.”

36. “Nessa casa moram 12
pessoas que só tem uma
perna, igual Saci.”

37. P: Não eram 12 pés?
A: Sim, mas o gato fugiu e o avô é cadeirante.

38. RESOLUÇÃO DE PROBLEMAS NA SALA DE AULA
ESTIMULAR ESTRATÉGIAS INDIVIDUAIS
VIVENCIAR AS SITUAÇÕES MATEMÁTICAS
DECIDIR SOBRE AS ESTRATÉGIAS
SOCIALIZAR AS ESTRATÉGIAS UTILIZADAS

39. NA RESOLUÇÃO DE UMA SITUAÇÃO-PROBLEMA
O ALUNO PRECISA:
INTERPRETAR A SITUAÇÃO –PROBLEMA VIVENCIADA.
COMPREENDER O ENUNCIADO DO PROBLEMA
ESTABELECER RELAÇÕES ENTRE O ENUNCIADO E OS
CONHECIMENTOS MATEMÁTICOS

40. FATORES QUE LEVAM OS ALUNOS A
ERROS NA RESOLUÇÃO DE PROBLEMAS
Duas naturezas de “erros”:
Os de natureza linguística: decorrentes das
dificuldades de compreensão de textos, considerando
que o enunciado dos problemas é um texto, seja ele
apresentado de modo oral ou escrito.
 Os de natureza matemática: decorrentes de
limitações na compreensão de conceitos envolvidos
impedindo o estabelecimento das relações necessárias
para a solução do problema.

41. SITUAÇÕES ADITIVAS E
MULTIPLICATIVAS
NO CICLO DE
ALFABETIZAÇÃO

42. VOCÊ JÁ OUVIU ESSAS PERGUNTAS?
 Professor, que conta tem que fazer?
 É de mais ou de menos?
 É de vezes ou de dividir?

43. Teoria dos campos conceituais
Gérard Vergnaud
CAMPO CONCEITUAL: um conjunto de situações cujo
domínio requer uma variedade de conceitos, de
procedimentos e de representações simbólicas em
estreita conexão.
 Estruturas aditivas: medida, transformação,
comparação, diferença, inversão, adição, subtração,
número natural, número relativo...
 Estruturas multiplicativas: multiplicação, divisão,
número racional...

44. Cálculo relacional: Compreensão das relações e
propriedades envolvidas nos problemas.

45. Vergnaud (2009) afirma que conceitos não
podem ser compreendidos de modo isolado,
mas sim a partir de campos conceituais.

46. COMPOSIÇÃO COMPARAÇÃO
TRANSFORMAÇÃO

47. PROBLEMAS DE COMPOSIÇÃO
Situações que envolvem parte-todo: juntar uma
parte com outra parte para obter o todo, ou
subtrair uma parte do todo para obter a outra
parte

48. Exemplo de Composição
1)Todo desconhecido
Ex: Carolina e João Pedro colecionam miniaturas de
garrafas de refrigerante, Carolina tem 19
miniaturas e João Pedro tem 16 miniaturas.
Quantas miniaturas eles têm juntos?
2) Parte desconhecido
Ex: Carolina e João Pedro têm juntos 35 miniaturas
de garrafas de refrigerante. Carolina tem 19
miniaturas. Quantas João Paulo tem?

49. Problemas de Transformação
Situações em que no estado inicial tem-se uma
quantidade que se transforma (por acréscimo
ou decréscimo), chegando ao estado final com
outra quantidade.

50. Exemplos de Transformação
1) Resultado desconhecido – situação de acréscimo
Ex: Daniela possui uma coleção de chaveiros. Ela tinha 15
chaveiros. Sua tia lhe deu de presente 17 chaveiros. Quantos
ela tem agora?
2) Transformação desconhecida – situação de decréscimo
Ex: Carla tinha 4 figurinhas. Ganhou algumas de seu tio e ficou
com 9 figurinhas. Quantas ela ganhou do tio?
3) Estado Inicial desconhecido – situação de decréscimo
Ex.: A mãe de Adriana tinha alguns bombons. Ela deu 5 para
seus filhos e ainda ficou com 4. Quantos bombons a mãe de
Adriana tinha?

51. Problemas de comparação
Comparam duas quantidades, uma chamada
referente e a outra, o referido. (São
confrontadas duas quantidades)

52. Exemplos de Comparação
1) Diferença desconhecida Ex: Na cantina de nossa escola há 36
pacotes de biscoitos de chocolate e 17 pacotes de biscoito de
morango. Quantos pacotes de morango há a menos?
2) Quantidade maior desconhecida Ex: Na cantina de nossa
escola há alguns pacotes de biscoitos de chocolate e 17 pacotes
de biscoitos de morango. Se há 19 pacotes de biscoito de
chocolate a mais. Quantos pacotes de chocolate há?
3) Quantidade menor desconhecida Ex: Na cantina de nossa
escola há 36 pacotes de biscoitos de chocolate e 19 pacotes de
biscoito de morango a menos. Quantos pacotes de morango há?

53.  OBSERVE ALGUMAS SITUAÇÕES
PROBLEMAS E RESOLVA

54. LEITURA DE IMAGENS
CRIANÇA CARTA

55. LEITURA DE IMAGENS
CRIANÇA CARTA
Por meio desta imagem pode-se explorar a oralidade das crianças e a
interpretação dos fatos que se sucedem.
São três crianças jogando, a que ficou com menos cartas perdeu e saiu do
jogo após juntarem as cartas. As duas que ficaram continuaram jogando e
empataram, pois a quantidade de cartas é a mesma. Evidentemente, há outras
interpretações e a professora pode explorar por meio de perguntas, o que
relaciona a leitura à resolução de Problemas.

56. OBRA DE ARTE "Roda" de Milton Dacosta em 1942

57. OBRA DE ARTE "Roda" de Milton Dacosta em 1942
Há muitas outras obras de arte a serem exploradas, não necessariamente com
a contagem de elementos ou formas geométricas.
Neste caso, o que se pode explorar?
Dentre outras possibilidades, as noções de direita e esquerda, onde
brincavam, que horário aconteceu a brincadeira, como estava o tempo (havia
sol, pois aparece a sombra), etc.

58. TIRINHAS
As tirinhas também apresentam ideias matemáticas que se transformam em
interessantes problemas.
Por exemplo, neste caso, qual foi a brilhante ideia de Magali?

62. ERA UMA VEZ ...
MUITOS PROBLEMAS DE UMA VEZ

64. 1
QUEM SÃO?
2
ONDE FORAM?
3
O QUE
COMPRARAM?
4 5
QUANTO
CUSTOU?
COMO
ACABOU?
6
COMO
RESOLVER?

65. Problemas “sem contas”:
Joana ganhou um gatinho recém-nascido que, em
pouco tempo, cresceu e se transformou num belo
gato. Agora, Joana está querendo saber quantos
quilos pesa seu bichinho, o problema é que ela não
consegue convencer o bicho a ficar quieto sobre a
balança da farmácia, foi então que Joana pensou muito
e "bolou" um sistema infalível para resolver o problema.
E você, como faria para resolvê-lo?

66.  Problemas com excesso de dados
Hemengardos é um “girafo”. Ele adora gravatas-borboleta.
Diz que elas valorizam seu pescoço.
Hemengardos tem vinte e uma gravatas lisas,
quinze de bolinhas, trinta e quatro listradas, oito
de estampados diversos, dezesseis floridas e
trinta cachecóis. Quantas gravatas Hemengardos
têm?
Caderno 1 (p.29)

67.  Problemas “sem perguntas”
CAMILA TEM 19 FIGURINHAS, BRUNO TEM 22.
Explorar as possibilidades de criação de situações...
Quem tem mais figurinhas?
Quantas figurinhas Bruno tem a mais do que Camila?
Quem tem menos figurinhas?
Quantas figurinhas Camila tem a menos do que Bruno?
Quantas figurinhas eles têm juntos?

68.  Só com as “perguntas”
QUANTOS DOCES SOBRARAM?
QUANTOS QUILÔMETROS FALTAM PARA
COMPLETAR A VIAGEM?

69. Construir o enunciado a partir da
“resposta”.
TENHO 55 FIGURINHAS.
RECEBI DE TROCO 2 REAIS.
GANHEI 15 PONTOS NO FINAL DO
JOGO.
SOBROU METADE DO BOLO.

70.  Completar enunciados.
UMA DOCEIRA FEZ PARA UMA
ENCOMENDA _______ BRIGADEIROS. SE
ELA COBRA ______ REAIS POR UMA
DEZENA DE DOCES. QUANTO ELA
RECEBEU PELO TRABALHO?

71. Problemas em tiras...
E não conseguia vendê-las
A notícia se espalhou e
Vendeu ___ toalhas. Ai, o dono abaixou o preço
Uma loja de tecidos tinha Ele vendeu ____
Quantas toalhas À tarde
Na manhã deste dia,
Sobraram no estoque? 382
790 1 700
Um estoque de ____toalhas

72. Uma loja de tecidos tinha um estoque de 1_ _7_0_0toalhas
e não conseguia vendê-las. Ai, o dono abaixou o preço.
Na manhã deste dia, vendeu _3_8_2__ toalhas.
A notícia se espalhou e à tarde ele vendeu ______.
Quantas toalhas sobraram no estoque?
790

73. A Resolução de Problemas e a superação da
perspectiva da simples “reprodução de
procedimentos”.
conhecimentos sempre estão inseridos em contextos;
a seleção sobre os contextos, as aproximações as experiências vividas pelos
alunos determina o grau de envolvimento das crianças com as questões;
estimular os alunos a questionarem suas respostas, os dados e o enunciado
do problema;
estes dados devem instigar os alunos para a criação de novos
Problemas;(p. 12)

74. JAMAIS ESQUECER!
 Explorar todas as ideias das operações por
meio da Resolução de Problemas...
 Mais problemas e menos operações isoladas e
sem significado...
Valorizar as estratégias das crianças...
 Nem tudo o que é para o professor deve ser
apresentado ao aluno...

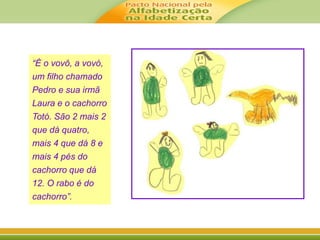
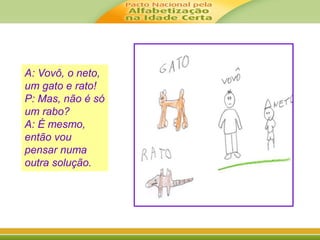
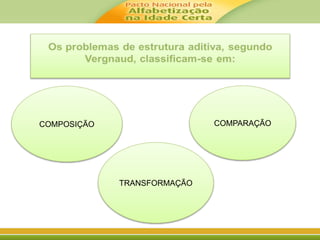
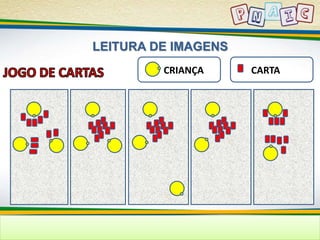
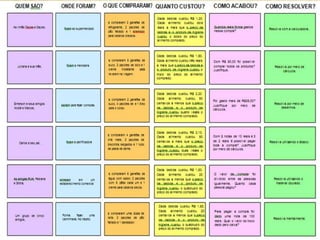
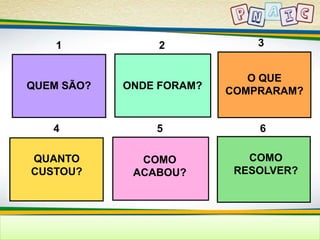
76. É importante lembrar que a compreensão dos
conceitos próprios das operações requer
coordenação com os diferentes sistemas de
representação.
[...]enfatizar o raciocínio não significa deixar de lado o
cálculo na resolução de problemas: significa calcular
compreendendo as propriedades das estruturas aditivas e
das operações de adição e subtração.”
(NUNES, CAMPOS, MAGINA E BRYANT, p. 56, 2005)

77. O que se propõe?
Cálculos numéricos estejam conectados ao
processo de compreensão progressiva do
Sistema de Numeração Decimal.
 Valorização da criação de estratégias pessoais
na resolução de problemas.
 Promoção de sua socialização.

78. Como você resolve?
- O cálculo necessário para
fornecer o troco de uma
compra no valor de R$ 48,00,
paga com uma cédula de
R$100,00?
- O preço a pagar por
8 metros e meio de fita
sendo que o metro
custa R$ 1,50.

79. Por que utilizar estratégias?
Proporcionam fluência no cálculo.
Possibilitam agilidade e menos erros.
Expressam uma compreensão rica e profunda do sistema
numérico.
Fornecem base sólida para o cálculo mental e estimativas.
Contribuem para um envolvimento no processo de “fazer
matemática”.

80. Nessa perspectiva, cada cálculo é um
problema novo e o caminho a ser
seguido é próprio de cada aluno, o que
faz com que para uns possa ser mais
simples e, para outros, mais complexo.

81. ESTRATÉGIAS DE CÁLCULO NÃO
SURGEM DO NADA.
PRECISAM SER TRABALHADAS E
ESTIMULADAS EM SALA DE AULA.

82. ESTIMULANDO AS ESTRATÉGIAS DE
CÁLCULO
- CONTAGEM-Procedimento
natural e bastante útil na resolução de
cálculos pelas crianças.
Algumas contagens importantes:
• contar para a frente;
• contar para trás;
•contar de 2 em 2, de 3 em 3, de 5 em 5, de 10 em 10;
•contar a partir de um determinado número

83. JOGO: COELHINHO PROCURANDO A TOCA

85. MEMORIZAÇÃO DE FATOS NUMÉRICOS
A tabuada pode agilizar processos de cálculos a
partir da memorização de resultados entre os fatores,
desde que:
A memorização deve ser consequência da adoção de
estratégias metodológicas que permitam a
construção/estruturação de regularidades entre os fatos
numéricos e a memorização dos mesmos por caminhos
diferentes da “decoreba” destituída de significado

86. Investigação Matemática na
Tabuada
João Pedro da Ponte sugere o desenvolvimento de
atividades investigativas, nas quais os alunos são
convidados a analisar padrões e regularidades
existentes nas operações. Observe:
Construa a tabuada do 3. O que encontra de curioso
nesta tabuada? Prolongue-as calculando 11 × 3, 12 ×
3, 13 × 3.... E formule algumas conjecturas.

87. construção de
recursos cognitivos
que auxiliam a
memorização
estabelecer relações
entre os fatos e
perceber
regularidades por
processos
investigativos
Pode-se pedir que os alunos façam registros escritos em forma de textos
das suas descobertas para que expressem as relacionem com as
propriedades do SND.

88. CONSTRUINDO A TÁBUA DE PITÁGORAS
x 1 2 3 4 5 6 7 8 9 10
1
2
3
4
5
6
7
8
9
10

89. JOGO: GATOS MALHADOS

90. REAGRUPAR EM DEZENAS OU CENTENAS
Construir sequências de
atividades investigativas...

91. FORMAÇÃO DA CENTENA

93. ALGORITMOS TRADICIONAIS
• O algoritmo tradicional das operações permite realizar
cálculos de uma maneira ágil e sintética.
• Modos de representar os processos operativos da
adição e da subtração pautados nas propriedades do SND.
É importante que a criança tenha se
apropriado das características do SND para
que compreenda os processos sequenciais
dos algoritmos.

94. O material dourado, o ábaco e o Quadro Valor
Lugar (QVL), são recursos que podem ser
utilizados, para favorecer a compreensão dos
algoritmos tradicionais.

95. ÁBACO
• Historicamente: como o precursor da
calculadora .
• Há diferentes modelos de ábaco, todos eles
com o mesmo princípio constitutivo do SND que
permite o trabalho centrado no valor posicional
do número.
• Sugere-se atividades com o ábaco aberto e
apenas até a ordem das unidades de milhar.

96. Material Dourado
A possibilidade de explorar propriedades do SND,
tais como:
a base 10
a composição aditiva e multiplicativa
explorar trocas e composição/decomposição
É importante salientar que o valor posicional do
algarismo não é tratado de forma explicita neste
recurso como o é no QVL e no ábaco.

97. Para pensar e discutir...
• Agrupamento e desagrupamento.
• Uso de material dourado e ábaco para resolver
algoritmos com “números grandes”.
• O cuidado com uso de recursos como o ábaco e
o material dourado.

99. ALGUMAS POSSIBILIDADES ...
Em situações reais, em que os números são muito
grandes ou muito pequenos, a utilização da
calculadora é recomendada. Isso porquê, o que
está em jogo é a resolução da situação-problema
real e não o uso de algoritmos.

100. SITUAÇÕES REAIS DE SALA DE AULA
Por exemplo, a tabela a
seguir foi construída
tendo como ponto de
partida dados coletados
por crianças que diziam
respeito à quantidade de
sorvetes que
conseguiram vender em
uma gincana.

101. Calculadora para construir e/ou sistematizar fatos
importantes das operações, ou mesmo para
disparar problemas.
- Encontrar o resultado de 4 x 5 sem utilizar
a tecla x.
- Fazer 20 ÷ 4, sem utilizar a tecla ÷
- Apertei a tecla 8, depois a tecla +, teclei
ainda um outro número, o sinal de = e
obtive 14. Que número apertei?
Quais as possibilidades para obter: a soma
10, ou 100 ou 1000.

102. Resolver o problema utilizando o algoritmo tradicional com o ábaco.
CAIXAS COM BOLINHAS DE TÊNIS
VÁRIAS CRIANÇAS RECOLHERAM BOLAS DE TÊNIS EM TRÊS
CAIXAS. SOMANDO A QUANTIDADE DE BOLAS DE DUAS DESSAS
CAIXAS, O TOTAL FOI 78. DESCUBRA ESSAS DUAS CAIXAS E
PINTE-AS:

103. Resolver o problema utilizando o algoritmo
tradicional com o material dourado.
MARIA COMPROU UMA BONECA POR R$ 24,00 E FICOU COM
R$ 17,00 REAIS NA CARTEIRA. QUANTO ELA POSSUIA ANTES
DE FAZER A COMPRA?

104. Resolver o problema utilizando o algoritmo
tradicional com o ábaco.
PROBLEMA EM TIRAS
ELE JÁ COLOU 29 FIGURINHAS.
QUANTAS FIGURINHAS ELE AINDA PRECISA COMPRAR PARA COMPLETAR SEU
ÁLBUM?
JOÃO COLECIONA FIGURINHAS DE FUTEBOL.
O ÁLBUM PARA ESTAR COMPLETO DEVE TER 56 FIGURINHAS.
ELE RESOLVEU COMPRAR TODAS AS FIGURINHAS QUE FALTAM EM SUA COLEÇÃO.

105. Resolver o problema utilizando o algoritmo
tradicional com o material dourado.
Completando o enunciado

106. OBRIGADA!