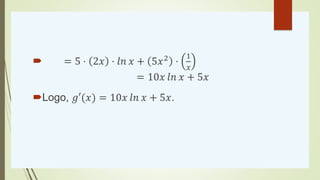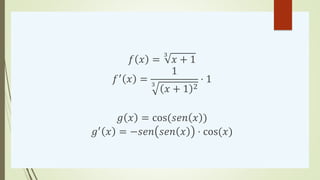[1] O documento discute limites de funções, incluindo limites laterais, limites infinitos e continuidade. [2] Apresenta exemplos de como calcular limites de funções polinomiais, racionais e irracionais quando x tende a um número. [3] Discutem-se também propriedades de limites e casos em que o limite não existe, como divisão por zero.



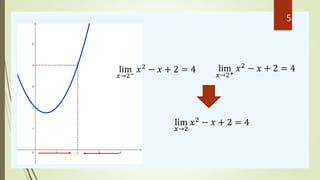





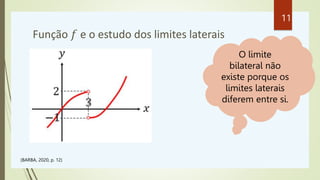
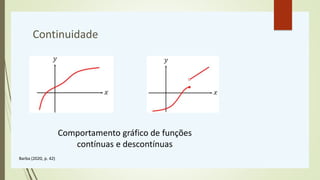
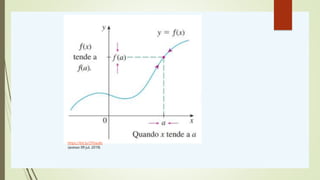
![Propriedades de Limites
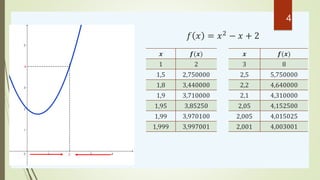
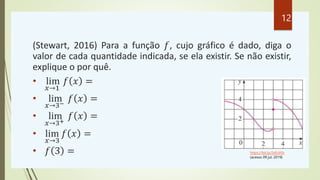
lim
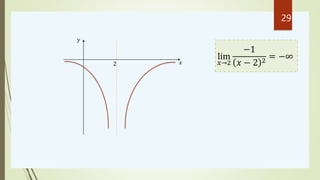
𝑥→𝑎
[𝑓 𝑥 ± 𝑔 𝑥 ] = lim
𝑥→𝑎
𝑓(𝑥) ± lim
𝑥→𝑎
𝑔(𝑥)
lim
𝑥→𝑎
[𝑐𝑓 𝑥 ] = 𝑐 ⋅ lim
𝑥→𝑎
𝑓(𝑥)
lim
𝑥→𝑎
[𝑓 𝑥 ⋅ 𝑔 𝑥 ] = lim
𝑥→𝑎
𝑓(𝑥) ⋅ lim
𝑥→𝑎
𝑔 𝑥
Seja c uma constante
e suponha que
existam os limites
lim
𝑥→𝑎
𝑓(𝑥) e
lim
𝑥→𝑎
𝑔(𝑥).
14](https://image.slidesharecdn.com/aula02clculointegralosmar-230123113946-3ccf00bc/85/Aula_02_Calculo_Integral_Osmar-pptx-14-320.jpg)




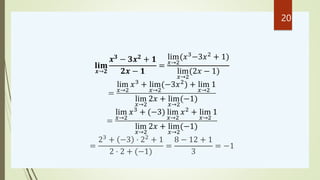

















![Regra do produto
A derivada de um produto de duas funções é a derivada
da primeira função vezes a segunda função mais a
primeira função vezes a derivada da segunda função.
Seja duas funções 𝑓 e 𝑔 deriváveis, então
𝑑
𝑑𝑥
𝑓 𝑥 𝑔 𝑥 =
𝑑
𝑑𝑥
𝑓 𝑥 𝑔 𝑥 + 𝑓 𝑥
𝑑
𝑑𝑥
[𝑔 𝑥 ]](https://image.slidesharecdn.com/aula02clculointegralosmar-230123113946-3ccf00bc/85/Aula_02_Calculo_Integral_Osmar-pptx-42-320.jpg)
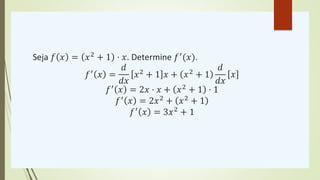
![Regra do quociente
A derivada de um quociente é o denominador vezes a derivada
do numerador menos o numerador vezes a derivada do
denominador, todos divididos pelo quadrado do denominador.
Seja duas funções 𝑓 e 𝑔 deriváveis, então
𝑑
𝑑𝑥
𝑓 𝑥
𝑔 𝑥
=
𝑑
𝑑𝑥
𝑓 𝑥 𝑔 𝑥 − 𝑓 𝑥
𝑑
𝑑𝑥
𝑔 𝑥
[𝑔(𝑥)]2](https://image.slidesharecdn.com/aula02clculointegralosmar-230123113946-3ccf00bc/85/Aula_02_Calculo_Integral_Osmar-pptx-44-320.jpg)