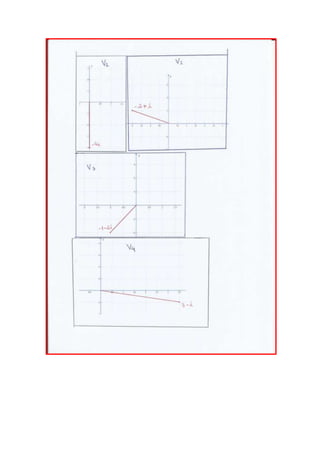
O documento apresenta exercícios de matemática sobre números complexos. Na questão 1, pede para encontrar as partes em que 4 pode ser dividido de forma que o produto seja igual a 5. Na questão 2, pede para resolver equações considerando números complexos. Na questão 3, pede para identificar afirmativas verdadeiras sobre números complexos e irracionais.

1. Curso de Engenharia - UNIVESP
Disciplina Matemática
Bimestre 1
Exercícios da semana 7 - vídeoaulas 27 e 28
Aula 27
Questão 1- Há infinitas possibilidades de dividirmos o número 4 em duas
partes. Algumas delas são bem óbvias como, por exemplo, 2 e 2 ou 1 e 3, e
outras, nem tanto, como 2,5 e 1,5 ou 1  2 e 3  2 .
Qual é, entre todas as infinitas possibilidades, aquela em o produto das partes
é igual a 5?
Condições:
x.y = 5
x + y = 4
Resolução:
x.y = 5  x = 5/y
x + y = 4  x = 4 – y
Logo,
5/y = 4 – y  -y2 + 4y – 5 = 0  Δ
= -4
-4 pode ser escrito como √4 . √-1  considerando √-1 = i temos:
-4 + 2.i  2 – i
-2
ou
-4 – 2.i  2 + i
-2

2. Questão 2 - - Resolva as equações considerando o conjunto dos números
complexos.
a) x2 – 6x + 10 = 0
Δ = -4  6 + 2.i  3 + i
2
ou
6 – 2.i  3 – i
2
b) x2 + 16 = 0
Δ = -4 ou + 4  4i ou -4i
c) x2 + x + 1 = 0
Δ = -3  √3 . √-1
- 1 + i√3
2
ou
-1 - i√3
2
Questão 3 - - Quais das seguintes afirmativas são verdadeiras?
a) Todo número complexo é também um número real.
Falsa
b) Um número inteiro qualquer, positivo ou negativo, é também um número
complexo.
Verdadeiro

3. c) Há números racionais que não pertencem ao conjunto dos números
complexos.
Falso
d) Os números irracionais não podem ser obtidos a partir da divisão de dois
números racionais.
Verdadeiro
e) Há números complexos que não são reais.
Verdadeiro
f) Não há número real que não seja complexo.
Verdadeiro
Aula 28
Questão 1- Represente no plano de Argand-Gauss os afixos seguintes
números complexos, desenhando, inclusive, o vetor que podemos traçar para
representar cada um deles.
v1 = - 4i v2 = - 2 + i v3 = -1 – 2i v4 = 3 – i
Resolução: