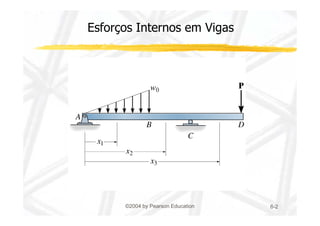
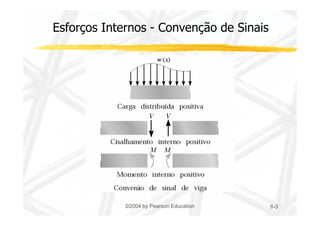
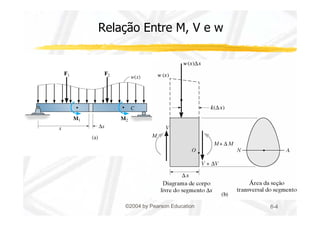
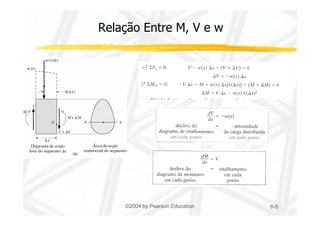
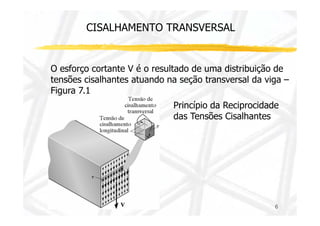
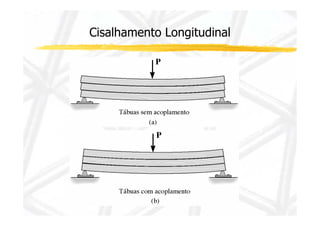
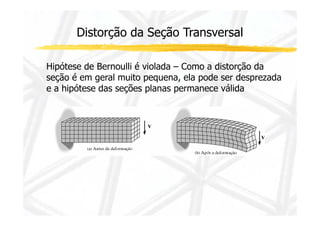
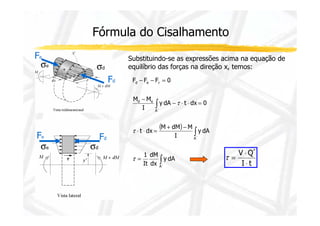
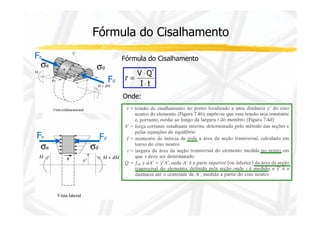
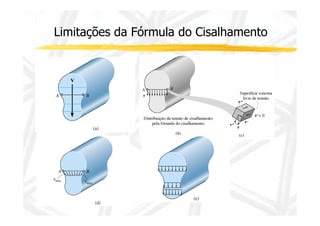
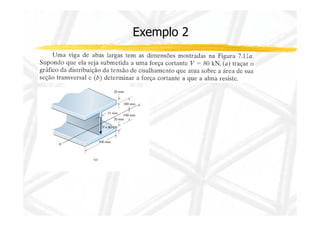
1. O documento discute cisalhamento transversal em vigas, apresentando a relação entre esforço cortante e tensão cisalhante.
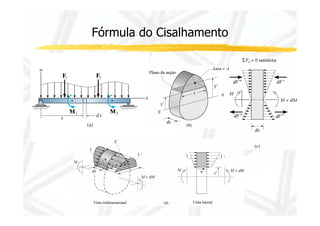
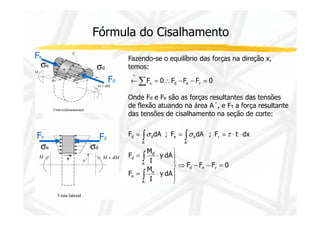
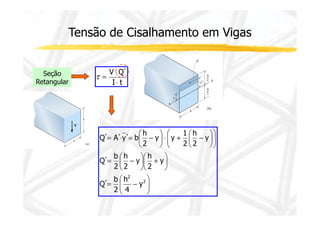
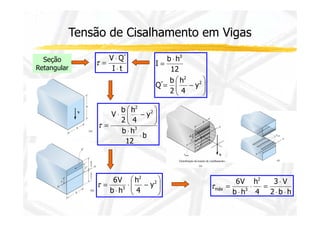
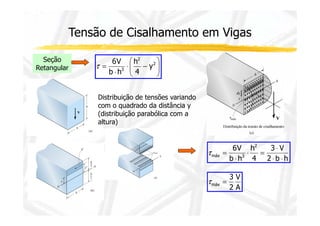
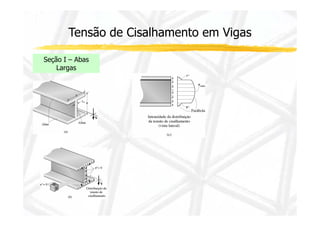
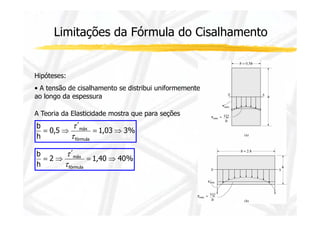
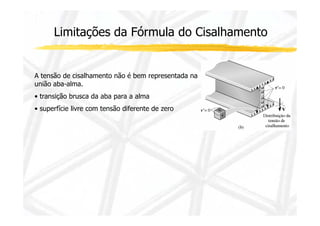
2. Apresenta a fórmula para calcular tensão cisalhante em seções retangulares e suas limitações.
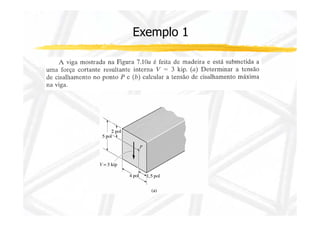
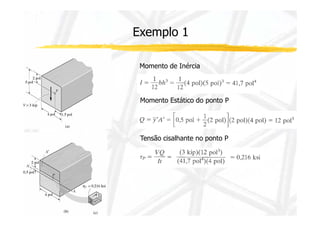
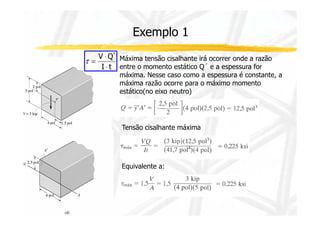
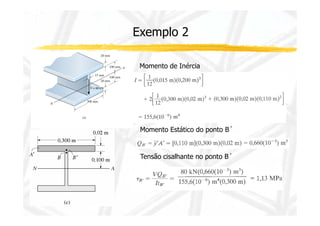
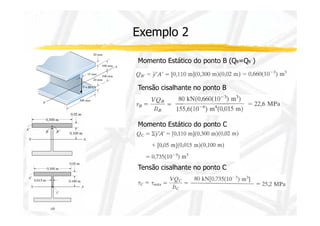
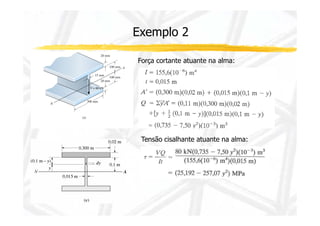
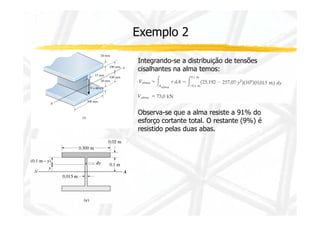
3. Inclui dois exemplos numéricos ilustrando cálculos de momento de inércia, momento estático, esforço cortante e tensão cisalhante em pontos de viga.